【拜小白的机器学习】4-机器学习的评估方法
这里的关键是:在现有的数据集合中获得可靠的“测试集数据”。这里有一个标准,就是测试集(用于评估)应该与训练集(用于学习)尽可能保持“互斥”。
常用的数据集划分方法有一下几种:
- 留出法(hold-out)
- 交叉验证法(k-fold cross validation)
- 自助法(bootstrap)
=================分割线==============
一、为什么要分开训练集与测试集
在机器学习中,我们是依靠对学习器的泛化误差进行评估的方法来选择学习器。具体方法如下:我们需要从训练集数据中产出学习器,再用测试集来测试所得学习器对新样本的判别能力,以测试集上的测试误差作为泛化误差的近似,来选取学习器。
通常我们假设训练集、测试集都是从样本集中独立同分布采样得到,且测试集、训练集中的样本应该尽可能互斥(测试集中的样本尽量不在训练集中有出现、尽量不在训练过程中被使用)。
测试样本为什么要尽可能不出现在训练集中呢?好比老师出了10道练习题给大家做,考试时候又用这10道练习题考试,这个考试成绩显然“过于乐观”,不能真实的反映同学的学习情况。我们是希望得到泛化性能强的模型,好比同学做完10道练习题能“举一反三”。
===============分割线====================
二、从样本集分得训练集、测试集的具体方法
当我们只有一个包含m个样例的样本集D={(x1,y1),(x2,y2),…,(xm,ym)},既要训练又要测试,我们就要对D进行适当处理,从中产出训练集S、测试集T。
1.留出法(hold out)
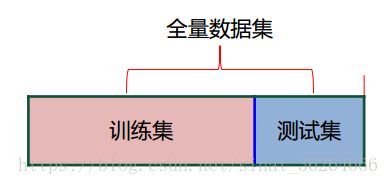
留出法(hold out):将全量数据集 D 划分为训练集 S 和测试集 T。
注意点:
- 保存数据分布一致性:即在划分数据集时,训练集 S 和测试集 T 中的类别比例要跟数据集 D 中的类别比例相似。(例如:分层采样)
- 多次重复划分(例如:100次随机划分)
- 测试集不能太大、不能太小(例如:为全量数据集的1/5~1/3)
===============分割线================
2.K折交叉验证(k-fold cross validation)
K折交叉验证(k-fold cross validation)
- 该方法先将数据集D划分为k个大小相似的互斥子集(即D = D1 or D2 or…or Di ),每个子集Di 在划分的时候应该保持数据分布的一致性,即从D中分层采样得到。
- 然后每次用k-1个子集的并集作为训练集,余下一个子集作为测试集,这样就可以获得k组训练/测试集。
- 进行k次训练和测试,返回k个测试结果的平均值。
注意点:
- 每份数据(数据子集)划分方式跟留出法一样,都尽可能保持数据分布的一致性,即从 D 中通过分层采样得到。
- 交叉验证法评估结果的稳定性和保真性很大程度上取决于k的取值。为强调这一点,通常交叉验证法也称为“k折交叉验证”。k常用取10,称为10折交叉验证;其他k值有5、20等。
- 与留出法相似,将样本集D划分为k个子集同样存在多种划分方式,为减小因样本划分不同而引入的误差,k折交叉验证通常要随机使用不同的划分重复p次,最终评估结果是这p次k折交叉验证结果的均值(例如10次10折交叉验证)。
- 如果样本集D包含m个样本,令k=m,就可以得到交叉验证法的特例——留一法(leave-one-out 简称LOO):留一法不受随机样本划分方式的影响,每个子集只包含一个样本,而使用的训练集与样本集只差一个样本,所以训练出来的模型与D的模型很相似。缺点在于如果样本集很大——100万条样本,就要训练出100万个学习器。
总结:我们理想中希望评估的是用样本集D训练出来的模型,但在留出法、交叉验证法中,由于都需要保留一部分样本用做测试,因此实际评估的模型所用的训练集比D小,这就必然引入误差。留一法受训练样本规模变化影响最小,但是计算复杂度高。下面介绍的方法既可减少训练样本规模不同造成的影响,又可比较高效的进行实验评估。
===================分割线=============================
3.自助法(bootstrap)
自助法(bootstrap):是一种基于“自助采样”的方法(bootstrap sampling),别称“有放回采样”、“可重复采样”。
假设样本集D包含m个样本,我们通过采样产生训练集d,具体方法如下:
- 每次随机从样本集D中选一个样本,拷贝加入训练集d中,再将该样本放回原样本集D,使得这个样本下次还有可能被采集到。
- 重复上述过程m次,我们就得到一个包含m个样本的训练集d。
- 剩下的样本(D - d)作为测试集。
注意点:
显然样本集D中一部分样本会在训练集d里多次出现,而另一部分样本不出现,这样的训练集d有2个特征:1.训练集与原样本集同规模;2.数据分布有所改变。
经计算,一个样本在m次采样始终不被采到的概率约为36.8%。将没有出现的样本就作为测试集,这样的测试结果,亦称为“包外估计”。
==============分割线=====================
总结:
留出法与交叉验证法都是使用分层采样的方式进行数据采样与划分,而自助法则是使用有放回重复采样的方式进行数据采样。
自助法在样本集D较小、难以有效划分训练/测试集时很有用。此外,自助法从初始样本集D中产生多个不同的训练集,这对集成学习等方法很有用。
然而,自助法产生的训练集改变了初始样本集的分布,这会引入估计误差。因此,当初始样本集足够时,留出法和交叉验证法更常用一些。
对于数据集小且可有效划分的时候最好使用留一法来进行划分,因为这种方法最为准确。
=================分割线================
参考文献;
机器学习中,从样本集合分得训练集、测试集的三种方法
机器学习模型性能评估方法笔记
机器学习模型评估方法
=================END==================