数据库设计 采用左右值编码来存储无限分级树形结构_1 预排序遍历树算法(modified preorder tree traversal algorithm )
如果你还在为数据库的无限分级树形结构而烦恼,可以试着使用 预排序遍历树算法(modified preorder tree traversal algorithm )
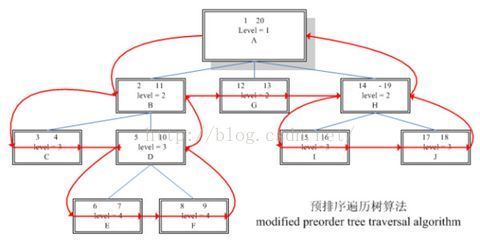
预排序遍历树算法有如下几个数据结构
1 N_LEFT 代表左 left
2 N_RIGHT 代表右 right
3 N_LEVEL 代表所在的层次 level
主要的是N_LEFT 和 N_RIGHT,重点关注左右值以及左右值的维护,以及查询的方便性
以下内容以MYSQL以及SQL操作为例子,展示这算法使用:
1) 建表语句:以文件夹的无限分级树形结构为例子
DROP TABLE IF EXISTS T_DIR;
CREATE TABLE T_DIR(
ID VARCHAR(32) NOT NULL UNIQUE,
V_NAME VARCHAR(50) NOT NULL UNIQUE,
V_PID VARCHAR(32),
N_LEFT BIGINT NOT NULL,
N_RIGHT BIGINT NOT NULL
);
唯一性约束只是为了方便检验。
2)初始化语句:
提示:32位UUID,MYSQL的生成方式:
REPLACE(UUID(),'-','')
但是,有个问题,同一个SQL用这种方式生成UUID会一样。
依照典型的结构,写的SQL的初始化语句如下:
INSERT INTO T_DIR(ID,V_NAME,V_PID,N_LEFT,N_RIGHT)
VALUES ('a2d3b4fdc4aa103498c55425bc3e045a','根目录',NULL,1,20),
('d2c7520ec4aa103498c55425bc3e045a','目录_1','a2d3b4fdc4aa103498c55425bc3e045a',2,11),
('e88ba151c4ab103498c55425bc3e045a','目录_1_1','d2c7520ec4aa103498c55425bc3e045a',3,4),
('930a67e7c4ab103498c55425bc3e045a','目录_1_2','d2c7520ec4aa103498c55425bc3e045a',5,10),
('2def8aa2c4ac103498c55425bc3e045a','目录_1_1_1','930a67e7c4ab103498c55425bc3e045a',6,7),
('3aaa5b6bc4ac103498c55425bc3e045a','目录_1_1_2','930a67e7c4ab103498c55425bc3e045a',8,9),
('87cc476ac4ac103498c55425bc3e045a','目录_2','a2d3b4fdc4aa103498c55425bc3e045a',12,13),
('e88ba20cc4ab103498c55425bc3e045a','目录_3','a2d3b4fdc4aa103498c55425bc3e045a',14,19),
('95388b6dc4ad103498c55425bc3e045a','目录_3_1','e88ba20cc4ab103498c55425bc3e045a',15,16),
('b6821366c4ad103498c55425bc3e045a','目录_3_2','e88ba20cc4ab103498c55425bc3e045a',17,18);
预排序遍历树算法的优点:
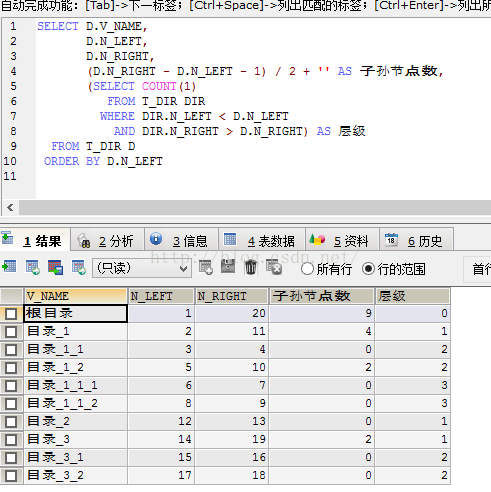
以目录_1_2为例:
1.获取子孙节点个数,子孙节点数据。
获取子孙节点个数
(N_RIGHT-N_LEFT-1)/2
获取子孙节点数据:
SELECT * FROM T_DIR WHERE N_LEFT>5 AND N_RIGHT<10;
2.获取祖先节点个数,祖先节点数据。
获取祖先节点个数
SELECT COUNT(1) FROM T_DIR WHERE N_LEFT<5 AND N_RIGHT>10;
获取祖先节点数据:
SELECT * FROM T_DIR WHERE N_LEFT<5 AND N_RIGHT>10;
3.获取自身层级(就是祖先节点个数)
SELECT COUNT(1) FROM T_DIR WHERE N_LEFT<5 AND N_RIGHT>10;
4.判断是否叶子(子孙节点个数为0则为叶子)
(N_RIGHT-N_LEFT-1)/2<1
以上为算法给查询带来的方便之处,下面讲述左右值的数据如何维护。
首先是插入:分成两种,根节点插入,非根节点插入
1)根节点插入:左值为1,右值为2.
2)非根节点插入:(先赋值,更新数据库数据,后插入)
临时变量temp=父节点的右值;
更新左右值:
UPDATE T_DIR SET N_LEFT = N_LEFT+2 WHERE N_LEFT>=temp;
UPDATE T_DIR SET N_RIGHT = N_RIGHT+2 WHERE N_RIGHT>=temp;
非根节点的左值为临时变量temp,
非根节点的右值为临时变量temp+1
然后是删除(先赋值,删除,更新数据库数据),叶子与非叶子节点都适用
1)临时变量temp_left=该节点的左值;
临时变量temp_right=该节点的右值;
2)获取该节点左右值差值(即自身+子孙节点)
临时变量temp_num= N_RIGHT-N_LEFT+1
3)删除以该节点为根的整颗树
DELETE
FROM T_DIR
WHERE N_LEFT N_LEFT >= temp_left
AND N_RIGHT <= temp_right;
4)更新数据库数据
UPDATE T_DIR SET N_LEFT = N_LEFT-temp_num WHERE N_LEFT> temp_right;
UPDATE T_DIR SET N_RIGHT = N_RIGHT-temp_num WHERE N_RIGHT>temp_right;
最后就是更新,也就是文件夹的移动
这块内容比较复杂点,另外写一章讲述
http://blog.csdn.net/jack_06_04/article/details/52443504
相关资料:
MySQL 左右值无限分类 预排序遍历树算法:http://my.oschina.net/bootstrap/blog/166805
左右值无限分类 预排序遍历树算法:modified preorder tree traversal algorithm http://blog.csdn.net/dreamer0924/article/details/7580278左右值编码来存储无限分级树形结构:http://blog.sina.com.cn/s/blog_63e167a20100thnh.html