随机模拟算法求解圆周率
圆周率(π)这个东西是从小学开始一直陪伴我们的,这里使用使用蒙特卡洛算法来产生大量的随机数求解π的近似值。
计算方式
首先我们知道 正方形的面积公式是S1 = a * a,圆形的面积S2 = π * r * r;
所以以圆的直径为正方形边长,可以得出π的表达式。
π = 4 * S2 / S1 这样一来,重点就是求解正方形和圆形的面积,这里使用在一正方形区域内圆内产生相应的随机点,
为了便于可视化分析,在圆内和圆外的点分别用不同的颜色来表示,最后圆内产生的点数就近似记作圆的面积,区域内的点数记作正方形的面积。
可视化分析-小数据集
这里用Java swing来求解。
首先看看Circle的model类
public class Circle {
private int x, y, r;
public Circle(int x, int y, int r){
this.x = x;
this.y = y;
this.r = r;
}
public int getX(){ return x; }
public int getY(){ return y; }
public int getR(){ return r; }
// 判断点是否包含在圆内
public boolean contain(Point p){
return Math.pow(p.x - x, 2) + Math.pow(p.y - y, 2) <= r*r;
}
}这里定义了圆的坐标,以及圆的半径。
然后看看点的model类
public class MonteCarloPiData {
private Circle circle;
private LinkedList points;
private int insideCircle = 0;
public MonteCarloPiData(Circle circle){
this.circle = circle;
points = new LinkedList();
}
public Circle getCircle(){
return circle;
}
// 得到点的数量
public int getPointsNumber(){
return points.size();
}
public Point getPoint(int i){
if(i < 0 || i >= points.size()) {
throw new IllegalArgumentException("out of bound in getPoint!");
}
return points.get(i);
}
//添加点到链表中
public void addPoint(Point p){
points.add(p);
// 计算圆内点的数量
if(circle.contain(p)) {
insideCircle++;
}
}
// π值的计算
public double estimatePi(){
if(points.size() == 0) {
return 0.0;
}
int circleArea = insideCircle;
int squareArea = points.size();
return (double)circleArea * 4 / squareArea;
}
} 接下来就是辅助类
public class AlgoVisHelper {
public static final Color Red = new Color(0xF44336);
public static final Color Green = new Color(0x4CAF50);
private AlgoVisHelper() {
// 绘制圆
public static void strokeCircle(Graphics2D g, int x, int y, int r){
Ellipse2D circle = new Ellipse2D.Double(x-r, y-r, 2*r, 2*r);
g.draw(circle);
}
// 填充圆
public static void fillCircle(Graphics2D g, int x, int y, int r){
Ellipse2D circle = new Ellipse2D.Double(x-r, y-r, 2*r, 2*r);
g.fill(circle);
}
// 绘制矩形
public static void strokeRectangle(Graphics2D g, int x, int y, int w, int h){
Rectangle2D rectangle = new Rectangle2D.Double(x, y, w, h);
g.draw(rectangle);
}
// 填充矩形
public static void fillRectangle(Graphics2D g, int x, int y, int w, int h){
Rectangle2D rectangle = new Rectangle2D.Double(x, y, w, h);
g.fill(rectangle);
}
// 设置颜色
public static void setColor(Graphics2D g, Color color){
g.setColor(color);
}
// 设置绘制宽度
public static void setStrokeWidth(Graphics2D g, int w){
int strokeWidth = w;
g.setStroke(new BasicStroke(strokeWidth, BasicStroke.CAP_ROUND, BasicStroke.JOIN_ROUND));
}
// 延长动画时间
public static void pause(int t) {
try {
Thread.sleep(t);
}
catch (InterruptedException e) {
System.out.println("Error sleeping");
}
}
}然后是渲染过程类
“`java
public class AlgoFrame extends JFrame{
private int canvasWidth;
private int canvasHeight;
public AlgoFrame(String title, int canvasWidth, int canvasHeight){
super(title);
this.canvasWidth = canvasWidth;
this.canvasHeight = canvasHeight;
// 实例化画笔 刷新视图
AlgoCanvas canvas = new AlgoCanvas();
setContentPane(canvas);
pack();
setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
setResizable(false);
setVisible(true);
}
public AlgoFrame(String title){
this(title, 1024, 768);
}
public int getCanvasWidth(){return canvasWidth;}
public int getCanvasHeight(){return canvasHeight;}
private MonteCarloPiData data;
public void render(MonteCarloPiData data){
this.data = data;
repaint();
}
private class AlgoCanvas extends JPanel{
public AlgoCanvas(){
// 双缓存
super(true);
}
@Override
public void paintComponent(Graphics g) {
super.paintComponent(g);
Graphics2D g2d = (Graphics2D)g;
// 抗锯齿
RenderingHints hints = new RenderingHints(
RenderingHints.KEY_ANTIALIASING,
RenderingHints.VALUE_ANTIALIAS_ON);
hints.put(RenderingHints.KEY_RENDERING, RenderingHints.VALUE_RENDER_QUALITY);
g2d.addRenderingHints(hints);
// 具体绘制
Circle circle = data.getCircle();
AlgoVisHelper.setStrokeWidth(g2d, 3);
AlgoVisHelper.strokeCircle(g2d, circle.getX(), circle.getY(), circle.getR());
/**
* 点在圆内 就绘制成红色
* 在圆外 绘制成绿色
*/
for(int i = 0 ; i < data.getPointsNumber() ; i ++){
Point p = data.getPoint(i);
if(circle.contain(p)) {
AlgoVisHelper.setColor(g2d, AlgoVisHelper.Red);
} else {
AlgoVisHelper.setColor(g2d, AlgoVisHelper.Green);
}
// 将点填充到圆内
AlgoVisHelper.fillCircle(g2d, p.x, p.y, 3);
}
}
@Override
public Dimension getPreferredSize(){
return new Dimension(canvasWidth, canvasHeight);
}
}
}
最后就是视图类了public class AlgoVisualizer {
private static int DELAY = 40;
private MonteCarloPiData data;
private AlgoFrame frame;
private int N;
public AlgoVisualizer(int sceneWidth, int sceneHeight, int N){
if(sceneWidth != sceneHeight) {
throw new IllegalArgumentException("This demo must be run in a square window!");
}
this.N = N;
Circle circle = new Circle(sceneWidth/2, sceneHeight/2, sceneWidth/2);
data = new MonteCarloPiData(circle);
// 初始化视图
EventQueue.invokeLater(() -> {
frame = new AlgoFrame("Get Pi with Monte Carlo", sceneWidth, sceneHeight);
new Thread(() -> {
run();
}).start();
});
}
// 动画主要逻辑
public void run(){
for(int i = 0 ; i < N ; i ++){
// 每次绘制100个点
if (i % 100 == 0) {
frame.render(data);
// 设置每次产生点的时间
AlgoVisHelper.pause(DELAY);
System.out.println(data.estimatePi());
}
int x = (int)(Math.random() * frame.getCanvasWidth());
int y = (int)(Math.random() * frame.getCanvasHeight());
data.addPoint(new Point(x,y));
}
}
public static void main(String[] args) {
int sceneWidth = 800;
int sceneHeight = 800;
// 设置点的数量
int N = 20000;
AlgoVisualizer vis = new AlgoVisualizer(sceneWidth, sceneHeight, N);
}
}
运行后,就可以看到点的绘制过程,最终结果如下

很显然 可以看到结果 精确到小数点后一位,点就无法绘制了,要想更加精确,试试更大的数据集。
### 无视图-大数据集
```java
public class MonteCarloExeperiment {
private int squareSide;
private int N;
private int outputInterval = 100;
public MonteCarloExeperiment(int squareSide, int N) {
if (squareSide <= 0 || N <= 0) {
throw new IllegalArgumentException("squareSide and N must large than 0!");
}
this.squareSide = squareSide;
this.N = N;
}
public void setOutputInterval(int interval) {
if (interval <= 0) {
throw new IllegalArgumentException("interval must be larger than 0!");
}
this.outputInterval = interval;
}
public void run() {
Circle circle = new Circle(squareSide/2,squareSide/2,squareSide/2);
MonteCarloPiData data = new MonteCarloPiData(circle);
for (int i=0;i < N;i++) {
if (i % outputInterval == 0) {
System.out.println(data.estimatePi());
}
int x = (int)(Math.random() * squareSide);
int y = (int)(Math.random() * squareSide);
data.addPoint(new Point(x,y));
}
}
public static void main(String[] args) {
int squareSide = 800;
int N = 10000000;
MonteCarloExeperiment exp = new MonteCarloExeperiment(squareSide,N);
exp.setOutputInterval(100000);
exp.run();
}
}这里设置了每次产生点的数量,其它逻辑差不多,去掉了视图的绘制, 这次用产生1千万随机数的方法来测试。
run一下,可以看到
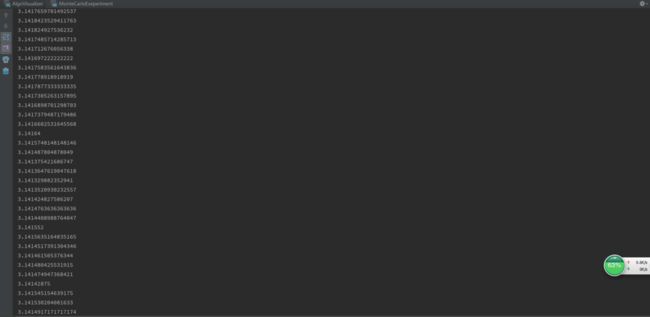
这次的结果,基本能精确到小数点后面4位、5位了,至此,计算过程就到这里了。
总结
这里使用蒙特卡洛算法,也就是产生更大的数据量是估算的值达到更精确。并且整个过程使用的是MVC的设计,再一次见识了计算机的魅力。