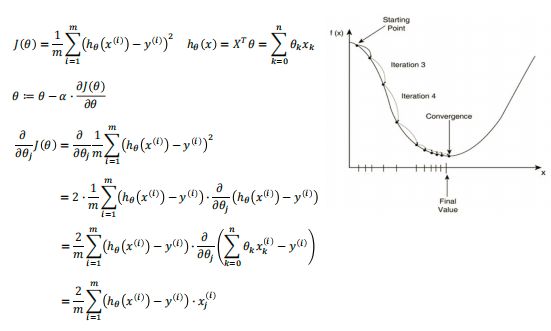
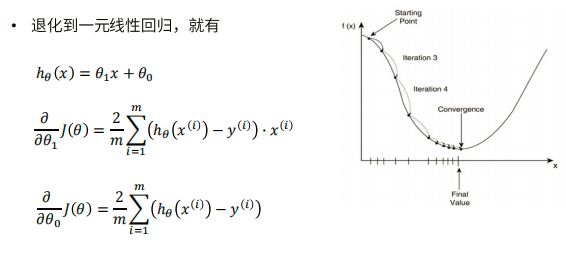
1、概述
梯度下降法和最小二乘法
相同点:
本质和目标相同:两种方法都是经典的学习算法,在戈丁已知数据的前提下利用求导算出一个模型(函数),使得损失函数最小,然后对给定的新数据进行估算预测
不同点:
损失函数:梯度下降可以选取其他损失函数,而最小二乘一定是平方损失函数
实现方法:最小二乘法是直接求导找出全局最小;而梯度下降是一种迭代法
效果:最小二乘法找到的一定是全局最小,但计算繁琐,且复杂情况下未必有解;梯度下降迭代计算简单,但找到的一般是局部最小,只有在目标函数是凸函数时才是全局最小;到最小点附近时收敛速度会变慢,且对初始点的选择极为敏感
2、代码实现
0.引入依赖
import numpy as np import matplotlib.pyplot as plt
1.导入数据(data.csv)
points = np.genfromtxt('data.csv',delimiter=',')
# 提取points中的两列数据,分别作为x,y
x=points[:,0] #取所有的第一列
y=points[:,1] #取所有的第二列
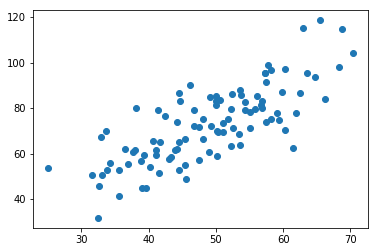
# 用plt画出散点图
plt.scatter(x,y)
plt.show()
2. 定义损失函数
# 损失函数是系数的函数,还要传入数据的x,y
def computer_cost(w,b,points):
total_cost = 0
M = len(points)
# 逐点计算平方损失误差,然后求平均值
for i in range(M):
x=points[i,0]
y=points[i,1]
total_cost += (y - w * x - b) ** 2
return total_cost/M
3. 定义模型的超参数
alpha = 0.0001 initial_w = 0 initial_b = 0 num_iter = 10
4.定义核心梯度下降算法函数
def grad_desc(points,initial_w,initial_b,alpha,num_iter):
w = initial_w
b = initial_b
# 定义一个list保存所有的损失函数值,用来显示下降的过程
cost_list = []
for i in range(num_iter):
cost_list.append(computer_cost(w,b,points))
w,b = step_grad_desc(w,b,alpha,points)
return [w,b,cost_list]
def step_grad_desc(current_w,current_b,alpha,points):
sum_grad_w = 0
sum_grad_b = 0
M = len(points)
# 对每个点,带入公式求和
for i in range(M):
x=points[i,0]
y=points[i,1]
sum_grad_w += (current_w * x + current_b - y) *x
sum_grad_b += current_w * x + current_b - y
# 用公式求当前梯度
grad_w = 2/M * sum_grad_w
grad_b = 2/M * sum_grad_b
# 梯度下降,更新当前的w和b
updated_w = current_w - alpha * grad_w
updated_b = current_b - alpha * grad_b
return updated_w,updated_b
5. 测试,运行梯度下降算法 计算最优的w和b
w,b,cost_list = grad_desc(points,initial_w,initial_b,alpha,num_iter)
print("w = " ,w)
print("b = " , b)
plt.plot(cost_list)
plt.show()
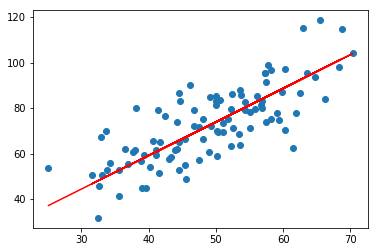
6. 画出拟合曲线
plt.scatter(x,y) # 针对每一个x,计算出预测的y值 pred_y = w * x + b plt.plot(x,pred_y,c='r') plt.show()