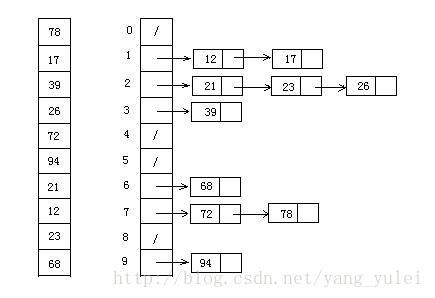
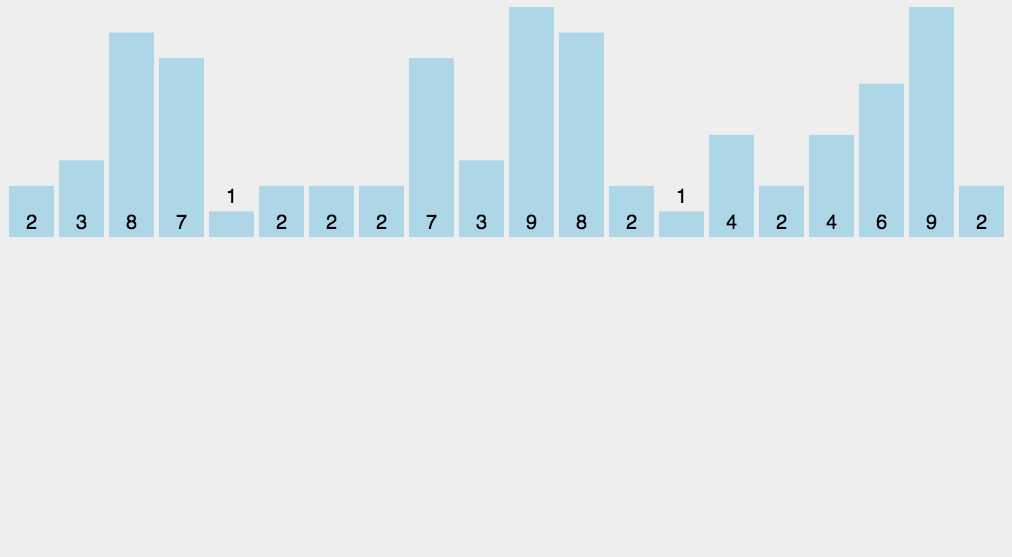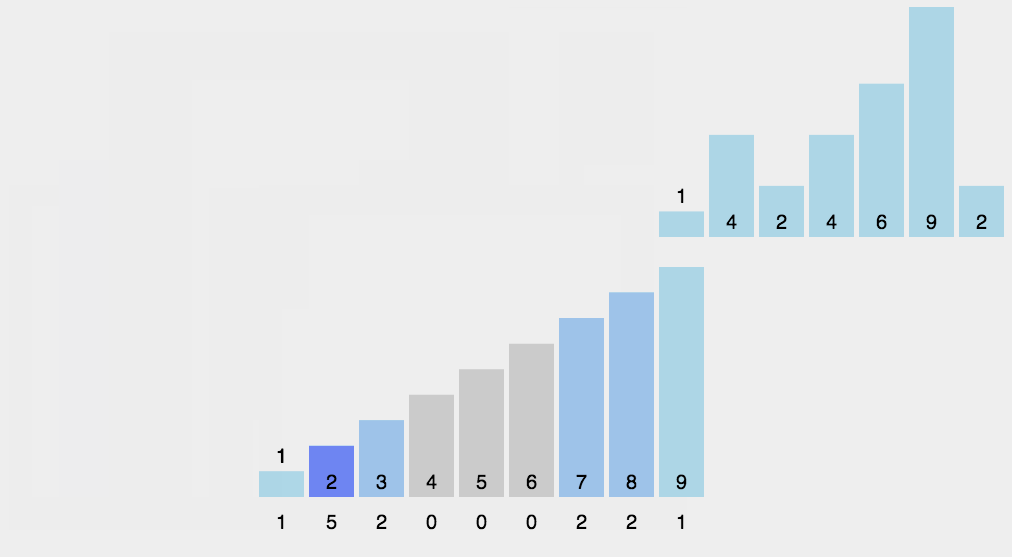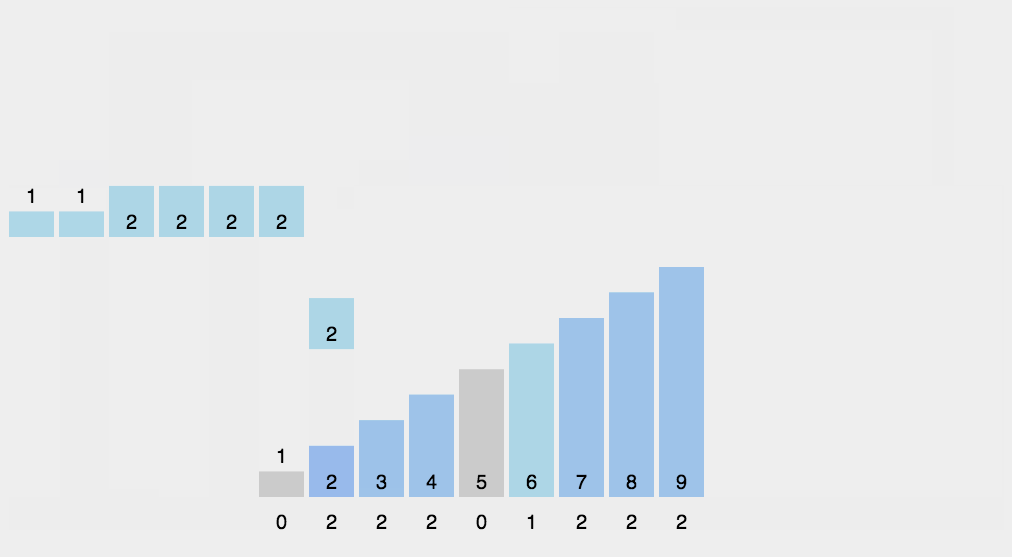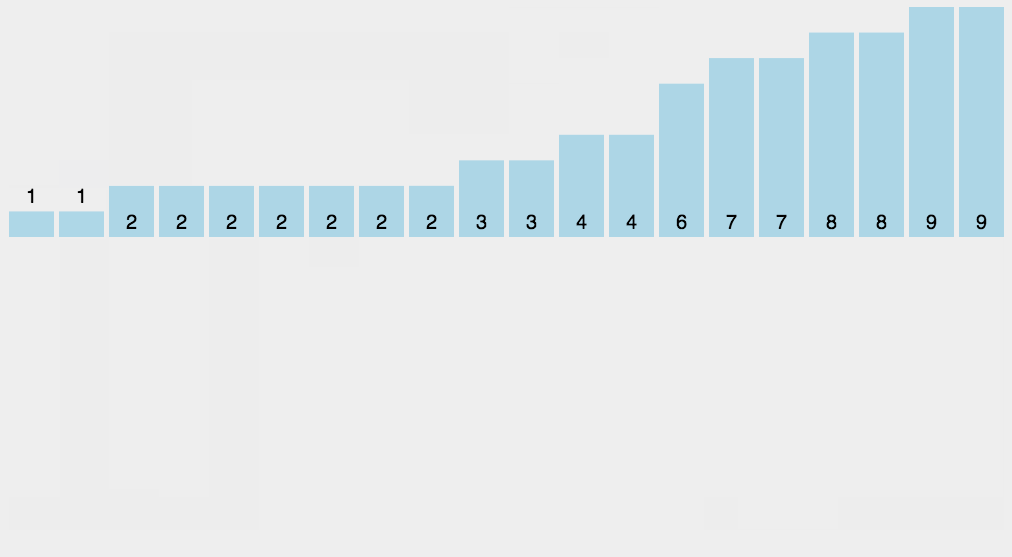算法模板——基础(未完待更)
基础数据结构和算法
- 1. 链表结构
-
- 1.1 单链表
- 1.2 双向循环链表
- 2. 图
-
- 2.1 存储结构
- 2.2 遍历
- 2.3 最短路径
- 2.4 有向图检测环
- 3. 树
-
- 3.1 二叉树存储结构
- 3.2 平衡二叉树(AVL)
- 4. 排序算法
-
- 4.1 快排
-
- 4.1.1 基础版
- 4.1.2 随机快排
- 4.2 堆排(大顶堆)
- 4.3 冒泡
-
- 4.3.1 鸡尾酒排序(冒泡的改进)
- 4.4 选排
- 4.5 插入
-
- 4.5.1 二分插入
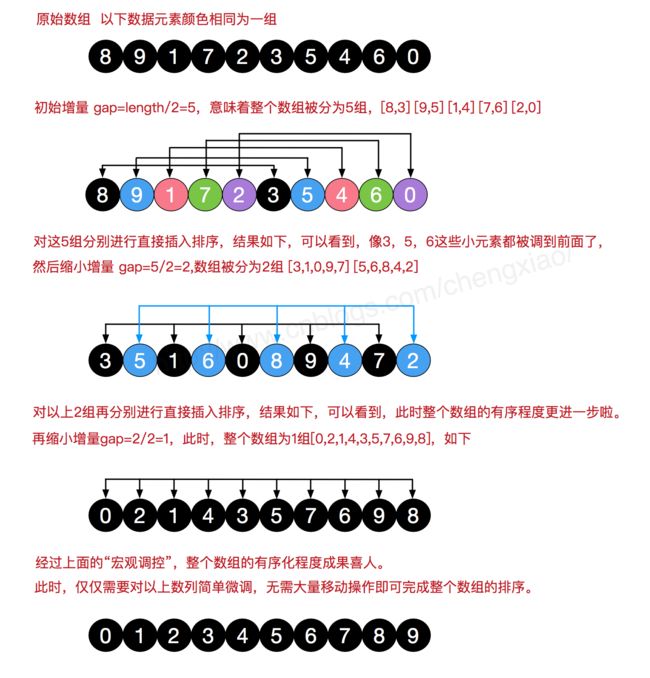
- 4.6 希尔
- 4.7 归并
- 4.8 计数排序
- 4.9 桶排
- 4.10 基数排序
- 5. 查找
-
- 5.1 二分查找
- 循环队列
1. 链表结构
1.1 单链表
C++
struct ListNode{
int val;
ListNode *next;
ListNode(int x): val(x), next(nullptr){
}
};
ListNode *CreateLinkList(int n){
ListNode *dummyhead = new ListNode(-1);
ListNode *p = dummyhead;
int x;
for(int i=0;i<n;i++)
{
cin >> x;
ListNode *tmp = new ListNode(x);
p->next = tmp;
tmp->next = nullptr;
p = tmp;
}
ListNode *head = dummyhead;
return head;
}
void PrintList(ListNode *head){
ListNode *p = head->next;
while(p!=nullptr)
{
cout << p->val;
if(p->next!=nullptr) cout << " -> ";
p = p->next;
}
cout << endl;
}
int GetLength(ListNode *head){
int cnt = 0;
ListNode *p = head->next;
while(p!=nullptr)
{
cnt++;
p = p->next;
}
return cnt;
}
bool IsEmpty(ListNode *head){
if(!head->next) return true;
return false;
}
ListNode *AddListNode(ListNode *head, int x){
// 头插入
ListNode *tmp = new ListNode(x);
tmp->next = head->next;
head->next = tmp;
return head;
}
ListNode *Find(ListNode *head, int x){
ListNode *p = head->next;
if(!p) return NULL;
while(p!=nullptr)
{
if(p->val==x) return p;
p = p->next;
}
return NULL;
}
bool DeleteListNode(ListNode *head, int x){
ListNode *tmp = Find(head, x);
if(!tmp) return false;
ListNode *p = head->next;
ListNode *pre = head;
while(p!=nullptr)
{
if(p->val==x)
{
pre->next = p->next;
delete p;
p = nullptr;
return true;
}
else
{
pre = p;
p = p->next;
}
}
}
Python
class ListNode:
def __init__(self, x):
self.val = x
self.next = None
class LinkList:
def __init__(self, node=None):
self.__head = node
def __len__(self):
cur = self.__head
cnt = 0
while cur:
cnt += 1
cur = cur.next
return cnt
def empty(self):
return self.__head == None
def add(self, x):
# 头插
node = ListNode(x)
node.next = self.__head
self.__head = node
def append(self, x):
# 尾插
node = ListNode(x)
cur = self.__head
if self.empty():
self.__head = node
else:
while cur.next:
cur = cur.next
cur.next = node
def remove(self, x):
cur = self.__head
pre = None
while cur:
if cur.x == x:
if cur == self.__head:
self.__head = cur.next
else:
pre.next = cur.next
break
else:
pre = cur
cur = cur.next
def find(self, x):
cur = self.__head
while cur:
if cur.val == x:
return True
return False
def printlist(self):
cur = self.__head
while cur:
print(cur.val)
cur = cur.next
1.2 双向循环链表
Python
class Node:
def __init__(self, val):
self.val = val
self.prev = self.next = None
class DCLinkedList:
def __init__(self):
self.dummy = Node(None, None)
self.dummy.next = self.dummy
self.dummy.prev = self.dummy
self.size = 0
def append(self, node):
# 尾插入
node.prev = self.dummy.prev
node.next = self.dummy
node.prev.next = node
self.dummy.prev = node
self.size += 1
def pop(self, node=None):
# 头删除
if self.size == 0: return
if node is None:
node = self.dummy.next
node.prev.next = node.next
node.next.prev = node.prev
self.size -= 1
return node
2. 图
2.1 存储结构
邻接表
C++
typedef struct ArcNode{
// 表结点
int adjvex;
ArcNode* next;
int info;
}ArcNode;
typedef struct VNode{
// 表头结点
int info;
ArcNode* first;
}VNode;
typedef struct Graph{
VNode adjList[maxsize];
int n, e;
};
Python
from collections import defaultdict
class Graph():
def __init__(self, v):
self.graph = defaultdict(list)
self.v = v
def addedge(self, u, v):
self.graph[u].append(v)
g = Graph(v)
g.addedge(x, y)
2.2 遍历
BFS
Python(邻接矩阵)
def BFS(graph, s):
q = []
q.append(s)
visited = set()
visited.add(s)
while q:
vertex = q.pop(0)
nodes = graph[vertex]
for node in nodes:
if node not in visited:
q.append(node)
visited.add(node)
Visit(vertex)
DFS
(1)借助栈
Python(邻接矩阵)
def DFS(graph, s):
st = []
st.append(s)
visited = set()
visited.add(s)
while st:
vertex = st.pop()
nodes = graph[vertex]
for node in nodes:
if node not in visited:
st.append(node)
visited.add(node)
Visit(vertex)
C++(邻接表)
void DFS(AGraph* g, int v){
ArcNode* p;
vector<int> st;
vector<int> visited(maxsize);
Visit(v);
visited[v] = 1;
st.push_back(v);
while(st)
{
int k = st.back();
p = g->adjList[k].fisrt;
while(p && visited[v->adjvex]) p = p->next;
if(!p) st.pop_back();
else
{
Visit(p->adjvex);
visited[p->adjvex] = 1;
st.push_back(p->adjvex);
}
}
}
(2)递归
Python(邻接矩阵)
def DFS(graph, s, path=[]):
path.append(s)
for i in graph[s]:
if i not in path:
DFS(graph, i, path)
return path
2.3 最短路径
迪杰斯特拉
inf = float('inf')
def dijkstra(graph_matix, s):
dis = graph_matix[s]
n = len(dis)
flag = [0 for _ in range(n)]
for i in range(n - 1):
mmin = inf
for j in range(n):
if flag[j] == 0 and dis[j] < mmin:
mmin = dis[j]
u = j
flag[u] = 1
for v in range(n):
if flag[v] == 0 and graph_matix[u][v]< inf:
if dis[v] > dis[u] + graph_matix[u][v]:
dis[v] = dis[u] + graph_matix[u][v]
return dis
佛洛依德
inf = float('inf')
def floyd(graph_matrix, s):
n = len(graph_matrix[0])
path = [[inf for _ in range(n)] for _ in range(n)]
for k in range(n):
for i in range(n):
for j in range(n):
if graph_matrix[i][j] > graph_matrix[i][k] + graph_matrix[k][j]:
graph_matrix[i][j] = graph_matrix[i][k] + graph_matrix[k][j]
path[i][j] = k
return graph_matrix, path
2.4 有向图检测环
着色法
对于图中的任意一个节点,我们定义三种状态,即:
「未搜索」:我们还没有搜索到这个节点;
「搜索中」:我们搜索过这个节点,但还没有回溯到该节点,即该节点还没有入栈,还有相邻的节点没有搜索完成);
「已完成」:我们搜索过并且回溯过这个节点,即该节点已经入栈,并且所有该节点的相邻节点都出现在栈的更底部的位置,满足拓扑排序的要求。
于是算法流程就是:
我们将当前搜索的节点 u u u 标记为「搜索中」,遍历该节点的每一个相邻节点 v v v:
-
如果 v v v 为「未搜索」,那么我们开始搜索 v v v,待搜索完成回溯到 u u u;
-
如果 v v v 为「搜索中」,那么我们就找到了图中的一个环,因此是不存在拓扑排序的;
-
如果 v v v 为「已完成」,那么说明 v v v 已经在栈中了,而 u u u 还不在栈中,因此 u u u 无论何时入栈都不会影响到 ( u , v ) (u, v) (u,v) 之前的拓扑关系,以及不用进行任何操作。
实际编程中没有必要用到栈,只用标记好状态就行
C++ 实现,图结构为矩阵
vector<int> visited;
bool invalid;
void dfs(int u) {
visited[u] = 1; // 将节点标记为「搜索中」
for(int v: edges[u])
{
if(visited[v]==0)
{
dfs(v);
if(invalid) return;
}
else if(visited[v]==1)
{
invalid = true;
return;
}
}
visited[u] = 2; // 将节点标记为「已完成」
}
bool iscyclic(vector<vector<int>& edges){
for(int i=0;i<edges.size() && !invalid;i++)
if(!visited[i]) dfs(i);
if(invalid) return true;
return false;
}
Python 实现, 图结构为邻接表
def dfs(self, u, color):
color[u] = "gray" # gary: this vertex is being processed
for v in self.graph[u]:
if color[v] == 'gray': return True
if color[v] == 'white' and self.dfs(v, color) == True:
# white: vertex is not processed yet
self.cyc.append(v)
return True
color[u] = "balck" # black:vertex and all its descendants are processed
return Fasle
def iscyclic(self):
for i in range(self.v):
color = ['white'] * self.v
if color[i] == 'white':
if self.dfs(i, color) == True:
return True
return False
拓扑排序
很简单就是完成拓扑排序之后还有节点未被加入到拓扑序列,那么就说明有环
C++实现,图结构为矩阵
vector<int> indeg;
vector<int> res;
bool iscyclic(vector<vector<int>>& edges){
queue<int> q;
for(int i=0;i<edges.size();i++)
if(indeg[i]==0) q.push(i);
while(!q.empty())
{
int u = q.front();
q.pop();
res.push_back(u);
for(int v: edges[u])
{
indeg[v]--;
if(!indeg[v]) q.push(v);
}
}
if(res.size()!=numCourses) return false;
return true;
}
Python实现,图结构为矩阵
def findcyc(G):
node_set = set()
r = len(G)
have_in_zero = True
while have_in_zero:
have_in_zero = False
for i in range(r):
if i not in node_set and not any([row[i] for row in G]):
node_set.add(i)
for j in range(len(G[i])):
if G[i][j]: G[i][j] -= 1
have_in_zero = True
break
return False if len(node_set) == r else True
Reference
- 算法札记 - 有向图找环(Python)
- 210. 课程表 II
3. 树
3.1 二叉树存储结构
C++
struct TreeNode {
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {
}
};
Python
Class TreeNode:
def __init__(self, value=0, left=None, right=None):
self.val = value
self.left = left
self.right = right
3.2 平衡二叉树(AVL)
C++
STL : : set,set的底层实现是红黑树
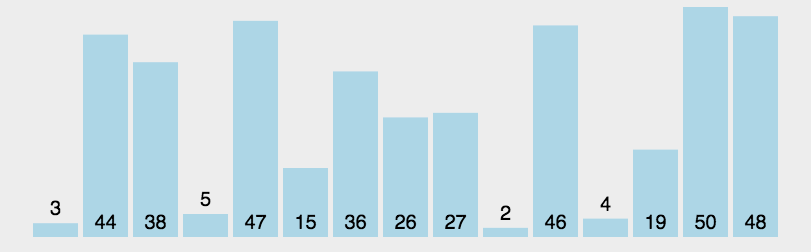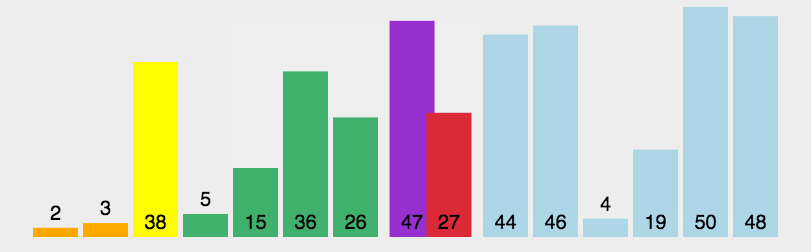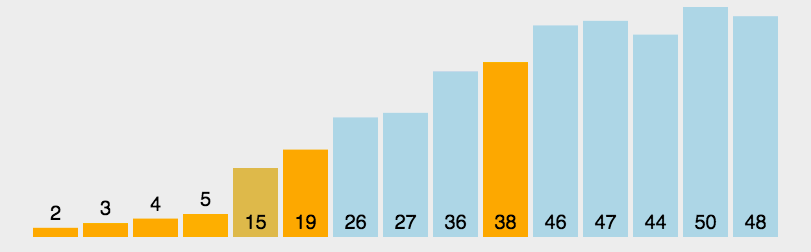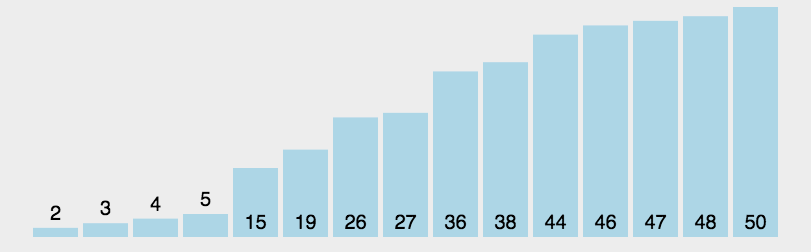
4. 排序算法
4.1 快排
4.1.1 基础版
int partition(vector<int>nums, int l, int r)
{
int pivot = nums[l];
int key = nums[l];
for(int i=l;i<=r;i++)
{
if(nums[i]<key) swap(nums[i], nums[++pivot]);
}
swap(nums[pivot], nums[l]);
return pivot;
}
void qicksort(vector<int>& nums, int l, int r)
{
if(l<r)
{
int pos = partition(nums, l, r);
quicksort(nums, l, pos-1);
quicksort(nums, pos+1, r);
}
}
void sortArray(vector<int>& nums)
{
if(nums.size()<=1) return;
quicksort(nums, 0, (int)nums.size()-1);
}
4.1.2 随机快排
解决普通快排在部分有序数组中进行排序效率低下的问题
class Solution {
public:
int partition(vector<int>& nums, int l, int r){
int pivot = l;
for(int i=l+1;i<=r;i++)
{
if(nums[i]<nums[l]) swap(nums[i], nums[++pivot]);
}
swap(nums[pivot], nums[l]);
return pivot;
}
int randomized_partition(vector<int>& nums, int l, int r){
int i = rand() % (r-l+1)+l;
swap(nums[l], nums[i]);
return partition(nums, l, r);
}
void randomized_quicksort(vector<int>& nums, int l, int r)
{
if(l<r)
{
int pos = randomized_partition(nums, l, r);
randomized_quicksort(nums, l, pos-1);
randomized_quicksort(nums, pos+1, r);
}
}
vector<int> sortArray(vector<int>& nums) {
srand((unsigned)time(NULL));
randomized_quicksort(nums, 0, (int)nums.size()-1);
return nums;
}
};
4.2 堆排(大顶堆)
class Solution {
public:
void adjustheap(vector<int>& nums, int i, int len){
int tmp = nums[i];
for(int k=i*2+1;k<len;k=k*2+1) // 从i节点的左节点开始重建
{
if(k+1<len && nums[k]<nums[k+1]) k++; // 如果左子节点小于右子节点,则让k指向右子节点
if(nums[k]>tmp) // 如果子节点大于父节点,将子节点赋值给父节点(不用进行交换)
{
nums[i] = nums[k];
i = k;
}
else break;
}
nums[i] = tmp; // 将tmp放到最终位置
}
void heapsort(vector<int>& nums){
//构建大顶堆
for(int i=nums.size()/2-1;i>=0;i--)
adjustheap(nums, i, nums.size());
// 弹出最大元素+调整堆
for(int i=nums.size()-1;i>=1;i--)
{
swap(nums[0], nums[i]); // 弹出最大顶堆的堆顶放在最后
adjustheap(nums, 0, i); // 重建大顶堆
}
}
vector<int> sortArray(vector<int>& nums) {
heapsort(nums);
return nums;
}
};
Python
借助heapq模块
class Solution:
def heapsort(self, nums):
h = []
for i in nums:
heapq.heappush(h, i)
return [heapq.heappop(h) for _ in range(len(h))]
def sortArray(self, nums: List[int]) -> List[int]:
nums = self.heapsort(nums)
return nums
4.3 冒泡
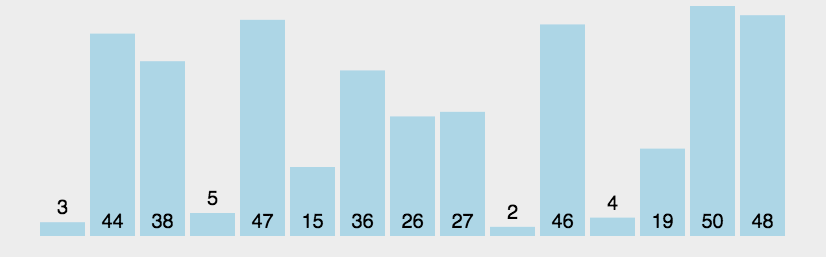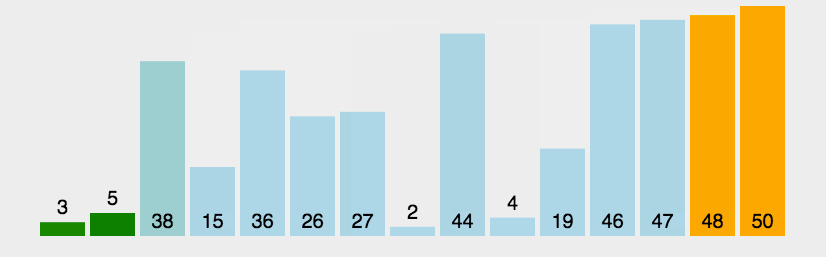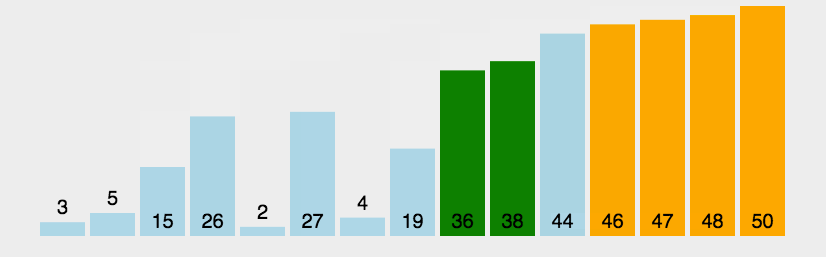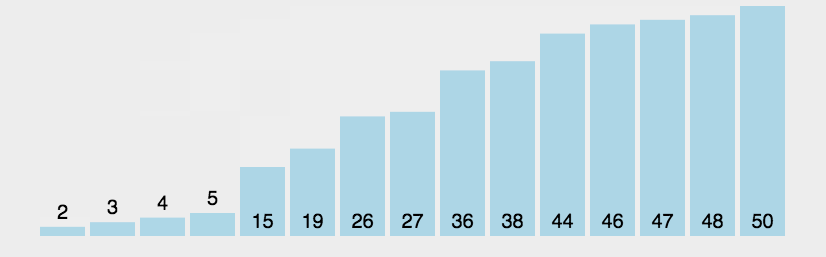
下面代码的实现不同于最简单的冒泡排序,这里加入了一个border用来记录上一次最后交换的那个位置,下一轮交换只需要进行到这个位置即可
void bubblesort(vector<int>& nums)
{
for(end=(int)nums.size-1;end>0;end--)
{
int border = 0;
for(int i=1;i<=end;i++)
{
if(nums[i-1]>nums[i])
{
swap(nums[i-1], nums[i]);
border = i;
}
}
end = border;
}
}
4.3.1 鸡尾酒排序(冒泡的改进)
鸡尾酒排序也叫定向冒泡排序,在大的往下沉的同时,小的往上浮
void cocktailsort(vector<int>& nums)
{
int l = 0, r = (int)nums.size()-1;
while(l<r)
{
for(int i=l;i<r;i++)
if(nums[i]>num[i+1]) swap(nums[i], nums[i+1]);
r--;
for(int i=r;i>l;i--)
if(nums[i]<nums[i-1]) swap(nums[i], nums[i-1]);
l++;
}
}
4.4 选排
void selectsort(vector<int>& nums)
{
for(int i=(int)nums.size()-1;i>0;i--)
{
int maxindx = 0;
for(int j=0;j<=i;j++)
if(nums[maxindx]<nums[j]) maxindx = j;
swap(nums[maxindx], nums[i]);
}
}
4.5 插入
void insertsort(vector<int>& nums)
{
for(int i=1;i<(int)nums.size();i++)
int j = i;
while(j>0 && nums[j] < nums[j-1])
swap(nums[j], nums[j-1]);
j--;
}
4.5.1 二分插入
void binaryinsertsort(vector<int>& nums)
{
for(int i=1;i<(int)nums.size();i++)
{
int key = nums[i];
in l = 0, r = i-1;
while(l<=r)
{
int mid = l+(l+r)/2;
if(nums[mid]>key) r = mid-1;
else l = mid+1;
}
// at the end of the process of biary, l = the index of the elements which is greater than key
for(int j=i-1;j>=l;j--) nums[j+1] = nums[j];
nums[l] = key;
}
}
4.6 希尔
void shellsort(vector<int>& nums)
{
int gap = (int)nums.size()>>1;
while(gap>0)
{
// sort every subsequence
for(int i=0;i<gap;i++)
{
// the porecess of insert sort
for(int j=i+gap;j<(int)nums.size;j+=gap)
{
int tmp = j;
while(tmp>i && nums[tmp]<nums[tmp-gap])
{
swap(nums[tmp], nums[tmp-gap]);
tmp -= gap;
}
}
}
gap >>= 1;
}
}
4.7 归并
void merge(vector<int>& nums, int left, int mid, int right)
{
vector<int> help(right-left+1);
int k = 0;
int p1 = left, p2 = mid+1;
while(p1<=mid && p2<=right)
help[k++] = nums[p1]<=nums[p2]?nums[p1++]:nums[p2++]; // 若左右两边相等,则先拷贝左边的,以实现稳定排序
while(p1<=mid) // 左边剩余部分
help[k++] = nums[p1++];
while(p2<=right) // 右边剩余部分
help[k++] = nums[p2++];
for(int i=0;i<k;i++)
nums[i+left] = help[i];
}
void mergesort(vector<int>& nums, int left, int right)
{
if(left>=right) return;
int mid = (left+right)/2;
mergesort(nums, left, mid);
mergesort(nums, mid+1, right);
// 这是一个优化,若nums[left, mid]nums[mid+1, right]已经有序,则不需要再排序了
if(nums[mid]>nums[mid+1]) merge(nums, left, mid, right);
}
vector<int> sortArray(vector<int>& nums)
{
mergesort(nums, 0, (int)nums.size()-1);
return nums;
}
4.8 计数排序
计数排序算法操作起来只有三步,看完秒懂!
- 根据待排序集合中最大元素和最小元素的差值范围确定申请的桶个数;
- 遍历待排序集合,将每一个元素统计到对应的桶中;(此步完成后每个桶里面的数字代表了此桶对应元素出现的次数。)
- 从小到大遍历一遍所有桶,如果桶中有元素,那么就往排序结果里添加上对应个数的该桶对应的元素。
void countsort(vector<int>& nums)
{
int mmin = INT_MAX;
int mmax = INT_MIN;
for(int num: nums)
{
mmin = min(mmin, num);
mmax = max(mmax, num);
}
vector<int> count(mmax-mmin+1);
for(int num: nums)
count[num-mmin]++;
int cur = 0;
for(int i=0;i<(int)count.size();i++)
{
while(count[i]>0)
{
nums[cur++] = i+mmin;
count[i]--;
}
}
}
4.9 桶排
void bucket_insert(list<int>& bucket, int val)
{
auto iter = bucket.begin();
// insert会在iter之前插入数据,以保证稳定排序
while(iter!=bucket.end() && val >= *iter) iter++;
bucket.insert(iter, val);
}
void bucketsort(vector<int>& nums)
{
int len = nums.size();
if(len<=1) return;
int mmin = nums[0], mmax = mmin;
for(int i=1;i<len;i++)
{
mmin = min(mmin, nums[i]);
mmax = max(mmax, nums[i]);
}
int k = 10;
int bucketnum = (mmax-mmin)/k + 1; // 向上取整,例如[0,9]有10个数,(9 - 0)/k + 1 = 1
vector<list<int>> buckets(bucketnum);
for(int i=0;i<len;i++)
{
int value = nums[i];
bucket_insert(buckets[(value-mmin)/k], value);
}
int indx = 0;
for(int i=0;i<bucketnum;i++)
{
if(buckets[i].size())
{
for(auto value: buckets[i])
nums[indx++] = value;
}
}
}
4.10 基数排序
void radixsort(vector<int>& nums)
{
if(!nums.size()) return;
int mmax = INT_MIN;
stringstream ss;
string s;
ss << mmax;
ss >> s;
int maxdigit = s.length(); // 最大位数
vector<list<int>> buckets(10);
int div = 1, mod = 10;
for(int i=0;i<maxdigit;i++)
{
for(int num: nums)
buckets[num%mod/div].push_back(num);
div *= 10;
mod *= 10;
int idx = 0;
for(int j=0;j<10;j++)
{
for(auto val: buckets[j])
{
nums[idx] = val;
idx += 1;
}
buckets[j].clear();
}
}
}
Reference
- 各种排序算法总结(全面)
- 排序算法之——三路快排分析
- 快排优化:随机快排、双路快排、三路快排
- 图解排序算法(三)之堆排序
5. 查找
5.1 二分查找
int binary_search(vector<int> nums, int target) {
int lo = 0, hi = nums.length - 1, mid = 0;
while (lo <= hi)
{
mid = lo + (hi - lo) / 2;
if (nums[mid] == target) return mid;
if (nums[mid] < target) lo = mid + 1;
else hi = mid - 1;
}
return -1;
}
在这里不做过多关于二分法内容的讨论,我将其放到了 算法模板——常用方法(未完待更) 中,有兴趣的可跳转参考。
循环队列
typedef struct
{
int nums[maxsize];
int front, rear;
}cycque
void Init(cycque &q){
q.front = q.rear = 0;
}
bool isEmpty(cycque q){
if(q.front==q.rear) return true;
return false;
}
bool isFull(cycque q){
if(a.front==(q.rear+1)%maxsize) return true;
return false;
}
bool Enque(cycque &q, int x){
if(isFull(q)) return false;
q.nums[q.rear] = x;
q.rear = (q.rear+1)%maxsize;
return true;
}
bool Deque(cycque &q, int &x){
if(isEmpty(q)) return false;
x = q.nums[front];
q.front = (q.front+1)%maxsize;
return true;
}