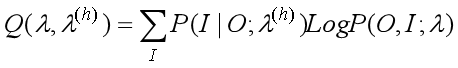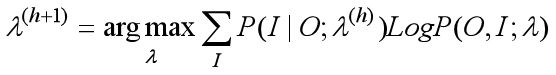隐马尔可夫模型(三)——鲍姆-韦尔奇算法(Baum-Welch算法)

一、问题回顾

模型参数的学习问题。即给定观测序列O={o₁,o₂,…o_T}，估计模型λ=(A,B,Π)的参数。这个问题的求解需要用到鲍姆-韦尔奇算法，我会在隐马尔可夫模型系列的第三篇博客中讲解，这个问题是HMM模型三个问题中最复杂的。
鲍姆-韦尔奇算法本质上就是EM算法，只不过它比EM算法出来的早，所以这里继续称它为鲍姆-韦尔奇算法。

二、监督学习算法求解模型参数

监督学习算法适用于观测序列和状态序列都已知的情况下，因为需要大量的训练数据，而人工标注训练数据的代价很高，所以该方法不是很常用。

假设训练数据为S对长度为 T 的状态序列 I = (i₁, i₂, … , i_T)及其观测序列 O = (o₁, o₂, … , o_T)组成的集合{(I₁, O₁), (I₂, O₃), … , (I_s, O_s)}，其中所有可能的状态集合为Q = {q₁, q₂, … , q_N}，所有可能的观测集合为V = {v₁, v₂, … , v_M}。

初始状态概率分布Π：
Π =[ π_i ]_N
取 I₁ 到 I_s 这S个状态序列的 i₁时刻的状态，组成一个长度为S的初始状态序列 C = (c₁₁, c₂₁, … , c_s1)，其中c_k1表示 I_k 这个状态序列在时刻 1 时的状态。
假设C( i )表示初始状态序列 C 中 状态 q_i 出现的次数，则 π_i 等于：

状态转移概率矩阵A：
统计 I₁ 到 I_s 这S个状态序列中从状态 q_i 转移到状态 q_j 的次数，用A_ij来表示。则可得：

所以得：
A = [a_ij]_N×N

观测生成概率矩阵B：
统计 (I₁, O₁) 到 (I_s, O_s) 这S对状态序列—观测序列中状态 q_j 生成观测 v_k 的次数，用B_jk来表示。则可得：

三、非监督学习算法求解模型参数

此处的非监督学习算法也就是本文打算重点讲解的鲍姆-韦尔奇算法。之所以说它是非监督学习算法，是因为鲍姆-韦尔奇算法求解模型参数时只用到了观测序列，而不用状态序列。

已知条件：
假设训练数据是长度为 T 的观测序列 O = (o₁, o₂, … , o_T)，所有可能的状态集合为Q = {q₁, q₂, … , q_N}，所有可能的观测集合为V = {v₁, v₂, … , v_M}。
未知条件：
假设长度为 T 的观测序列 O = (o₁, o₂, … , o_T) 所对应的状态序列为 I = (i₁, i₂, … , i_T)，它是未知的。

鲍姆-韦尔奇算法的原理：
鲍姆-韦尔奇算法使用的就是EM算法的原理，那么在第 h+1 次迭代时我们需要在E步求出联合分布P(O,I；λ)基于条件概率P(I | O；λ^(h))的期望，其中λ^(h)为第 h 次迭代时的模型参数，然后在M步最大化这个期望，就能得到更新的模型参数λ，它就是 h+1 次迭代得到的模型参数。接着不停的进行EM迭代，直到模型参数的值收敛为止。

1. 首先来看看E步， 联合分布P(O,I；λ)基于条件概率P(I | O；λ^(h))的期望表达式为：
   

2. 在M步，我们极大化上式，然后得到更新后的模型参数如下：

   
   通过不断的E步和M步的迭代，直到λ^(h+1)收敛。下面我们来看看鲍姆-韦尔奇算法的推导过程。

鲍姆-韦尔奇算法的推导：

已知条件：
假设训练数据是长度为 T 的观测序列 O = (o₁, o₂, … , o_T)，所有可能的状态集合为Q = {q₁, q₂, … , q_N}，所有可能的观测集合为V = {v₁, v₂, … , v_M}。

未知条件：
假设长度为 T 的观测序列 O = (o₁, o₂, … , o_T) 所对应的状态序列为 I = (i₁, i₂, … , i_T)，它是未知的。

模型参数：
λ=(A,B,Π)

首先来计算一下联合分布P(O, I；λ)的表达式：

求Q函数的表达式：

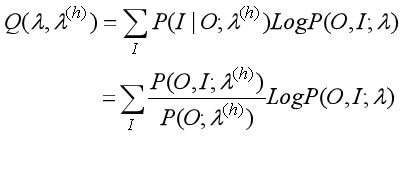
去掉常数P(O；λ^(h))，等价与求下式的极大化：

将P(O, I；λ)带入上式得最终的Q函数表达式为：

接下来极大化Q函数，求模型参数A,B,Π：
因为参数Π,B,A分别包含在Q函数的三个子式中，所以我们分别对Q函数的三个子式进行极大化来求参数。

(1)极大化第一个子式，求 π_i 的更新公式

先化简一下：

因为 π_i有约束，即 π₁+π₂+…+π_N = 1， 所以求出化简后的第一个子式的拉格朗日函数：

拉格朗日函数对 π_i 求导并令导数等于零得：
P(O，i₁= q_i；λ^(h+1)) + γπ_i = 0 （A式）
两边同时对 i 求累加和得：

将 γ 带入A式中得：

(2)极大化第二个子式，求 b_j(k) 的更新公式
先化简一下：

b_j(k)同样有约束条件，即b_j(1) + b_j(2) + … + b_j(M) = 1，所以求出化简后的第二个子式的拉格朗日函数：

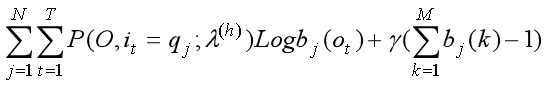
拉格朗日函数对 b_j(k) 求导并令导数等于零得：

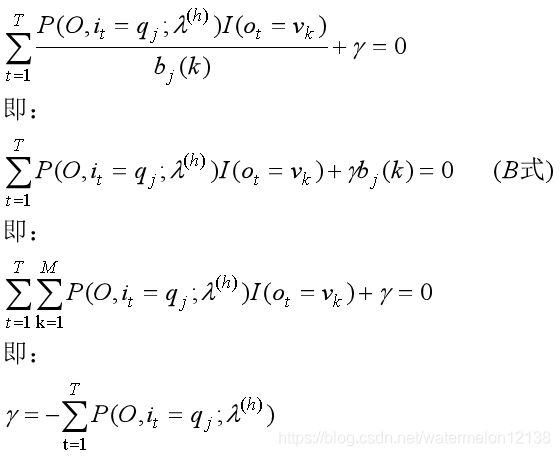
其中 I(o_t = v_k) 是指示函数。
将 γ 带入B式中得：

(3)极大化第三个子式，求 a_ij 的更新公式
这也是最麻烦的一步，坚持一下！
先化简第三个子式：

a_ij也有约束条件，即a_i1 + a_i2 + … + a_iN = 1，所以也要求出化简后的第三个子式的拉格朗日函数，然后拉格朗日函数再对 a_ij 求导数并令导数等于零。
这里就不再赘述了，直接上a_ij的更新公式：

一些概率的计算：
大家是不是也发现 π_i, a_ij, b_j(k)的更新公式比较繁重，所以这里介绍两种概率的记法，用此来简化 π_i, a_ij, b_j(k)的更新公式。

(1) 用 γ_t( i ) 表示在观测序列 O 给定的条件下，时刻 t 处于状态 q_i 的概率，即

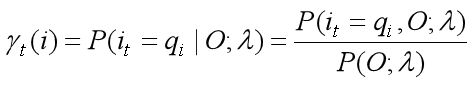
γ_t( i ) 也可以用前向概率和后向概率表示如下：

(2) 用 ξ_t( i, j )表示在观测序列 O 给定的条件下，时刻 t 处于状态 q_i 且时刻 t+1 处于 q_j的概率，即

ξ_t( i, j ) 也可以用前向概率和后向概率表示如下：

综上所述 π_i, a_ij, b_j(k)的更新公式可以写为：

鲍姆-韦尔奇算法流程：
输入：观测序列O = (o₁, o₂, … , o_T)
输出：模型参数
(1)初始化
对于h=0，初始化π_i⁽⁰⁾, a_ij⁽⁰⁾, b_j(k)⁽⁰⁾，得到模型λ⁽⁰⁾ = (Π⁽⁰⁾, A⁽⁰⁾, B⁽⁰⁾)。
(2)对 h = 1, 2, 3…，迭代更新参数：

其中上面各式的右端在模型参数λ^(h) = (Π^(h), A^(h), B^(h))和观测序列条件O的条件下计算。
(3)直到模型参数收敛，停止迭代。