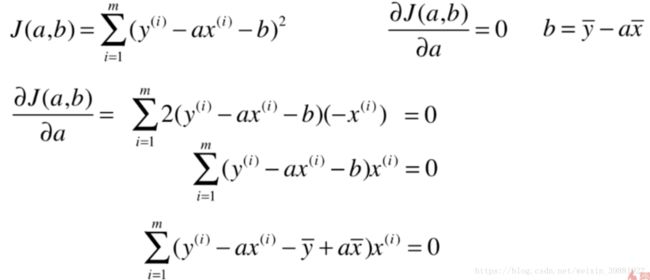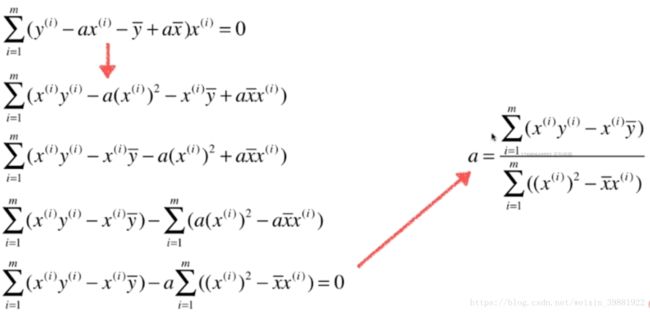线性回归---sklearn+python实现

简单线性回归

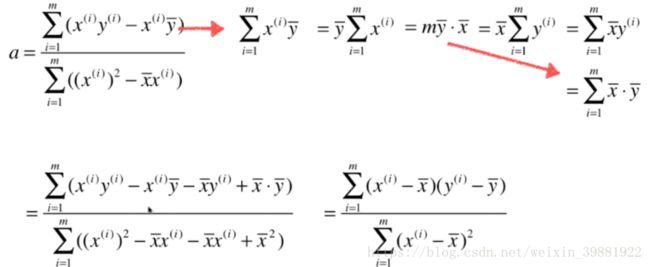
问题

思想

回到正题，对于简单线性回归有如下问题：

下面通过程序来实现简单的线性回归:

import numpy as np
import matplotlib.pyplot as plt
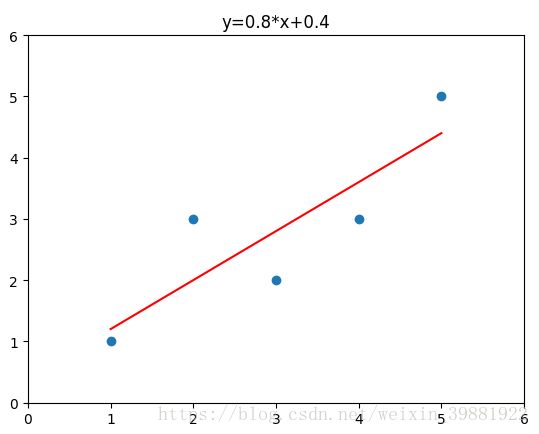
x=np.array([1,2,3,4,5])
y=np.array([1,3,2,3,5])
plt.scatter(x,y)
x_mean=np.mean(x)
y_mean=np.mean(y)
up=0.0
down=0.0
for x_i,y_i in zip(x,y):
    up+=(x_i-x_mean)*(y_i-y_mean)
    down+=(x_i-x_mean)**2
a=up/down
b=y_mean-a*x_mean
print(a,b)
y_hat=a*x+b
plt.plot(x,y_hat,c='red')
plt.axis([0,6,0,6])
plt.show()

创建自己的线性回归类：

import numpy as np
class SimpleLinearRegression1:
    def __init__(self):
        self.a_=None
        self.b_=None

    def fit(self,x_train,y_train):
        x_mean = np.mean(x_train)
        y_mean = np.mean(y_train)
        up = 0.0
        down = 0.0
        for x_i, y_i in zip(x_train, y_train):
            up += (x_i - x_mean) * (y_i - y_mean)
            down += (x_i - x_mean) ** 2
        self.a_ = up / down
        self.b_ = y_mean - self.a_ * x_mean
        return self

    def _predict(self,x_single):
        return x_single*self.a_+self.b_
    def predict(self,x_predict):
        return np.array([self._predict(x) for x in x_predict])

#改进，将for循环用向量化实现，增加效率
class SimpleLinearRegression2:
    def __init__(self):
        self.a_=None
        self.b_=None

    def fit(self,x_train,y_train):
        x_mean = np.mean(x_train)
        y_mean = np.mean(y_train)
        # up = np.dot((x_train-x_mean),(y_train-y_mean))
        # down =np.dot((x_train-x_mean),(x_train-x_mean))
        up = np.sum((x_train - x_mean)*(y_train - y_mean))
        down = np.sum((x_train - x_mean)*(x_train - x_mean))
        self.a_ = up / down
        self.b_ = y_mean - self.a_ * x_mean
        return self

    def _predict(self,x_single):
        return x_single*self.a_+self.b_
    def predict(self,x_predict):
        return np.array([self._predict(x) for x in x_predict])

from ML import SimpleLinearRegression
s=SimpleLinearRegression.SimpleLinearRegression2()
s.fit(x,y)
y_hat=s.predict(np.array([6]))
y_hat=s.a_*x+s.b_
plt.plot(x,y_hat,c='red')
plt.axis([0,6,0,6])
plt.title('y=%s*x+%s'%(s.a_,s.b_))
plt.show()

线性回归算法的评测

均方误差MSE	均方根误差RMSE(与用本同量纲)	平均绝对误差MAE

编程实现：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
#生成数据
boston=datasets.load_boston()
print(boston.DESCR)
print(boston.feature_names)
x=boston.data[:,5]
y=boston.target
x=x[y<50]
y=y[y<50]
#进行训练集和测试集划分
from ML.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(x,y,seed=666)
#进行简单的线性回归
from ML.SimpleLinearRegression import SimpleLinearRegression2
s=SimpleLinearRegression2()
s.fit(x_train,y_train)
print(s.a_,s.b_)
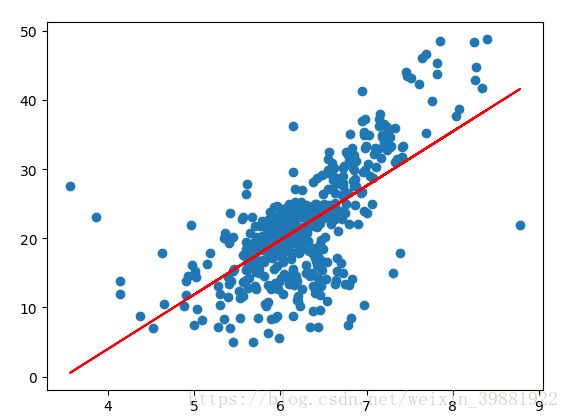
plt.scatter(x,y)
plt.plot(x,s.a_*x+s.b_,c='red')
plt.show()
#线性回归模型的评估指标
y_predict=s.predict(x_test)
#MSE
mse_test=np.sum((y_predict-y_test)**2)/len(x_test)
print(mse_test)

#RMSE
rmse_test=np.sqrt(mse_test)
print(rmse_test)

#MAE
mae_test=np.sum(np.absolute(y_predict-y_test))/len(x_test)
print(mae_test)

mse_test 24.1566021344
rmse_test 4.91493663585
mae_test 3.54309744095

sklearn中的MSE和MAE

from sklearn.metrics import mean_squared_error,mean_absolute_error
mean_squared_error(y_test,y_predict)
print('sk_mse_test',mse_test)
mean_absolute_error(y_test,y_predict)
print('sk_mae_test',mae_test)

sk_mse_test 24.1566021344
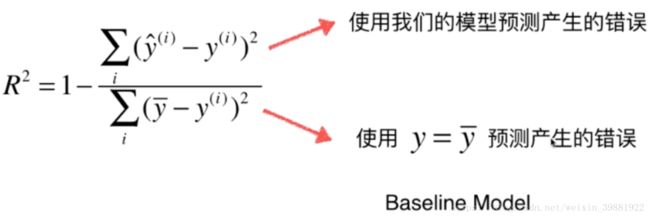
sk_mae_test 3.54309744095

更好的衡量线性回归的指标 R Squared

#R Square
R=1-mean_squared_error(y_test,y_predict)/np.var(y_test)
print(R)

R Square: 0.612931680394

使用sklearn计算R Square

from sklearn.metrics import r2_score
r2=r2_score(y_test,y_predict)
print('r2_score',r2)

r2_score 0.612931680394

import numpy as np
from .metrics import r2_score
class LinearRegression:
    def __init__(self):
        self.coef_=None  #系数
        self.interception_=None  #截距
        self._theta=None

    def fit_normal(self,X_train,y_train):
        x_b=np.hstack([np.ones((len(X_train),1)),X_train])
        self._theta=np.linalg.inv(x_b.T.dot(x_b)).dot(x_b.T).dot(y_train)
        self.coef_=self._theta[1:]
        self.interception_=self._theta[0]
        return self

    def predict(self,x_predict):
        x_b = np.hstack([np.ones((len(x_predict), 1)), x_predict])
        return x_b.dot(self._theta)

    def score(self,x_test,y):
        y_predict=self.predict(x_test)
        return r2_score(y_predict,y)

使用自己的类实现线性回归：

from sklearn import datasets
from sklearn.model_selection import train_test_split
from ML.LinearRegression import LinearRegression
boston=datasets.load_boston()
#使用全部的列
X=boston.data
y=boston.target
x=X[y<50]
y=y[y<50]
x_train,x_test,y_train,y_test=train_test_split(x,y,random_state=666)
L=LinearRegression()
L.fit_normal(x_train,y_train)
print(L)
print(L.coef_)
print(L.interception_)
score=L.score(x_test,y_test)
print(score)

使用sklearn实现线性回归

from sklearn.linear_model import LinearRegression
lin_reg=LinearRegression()
lin_reg.fit(x_train,y_train)
score=lin_reg.score(x_test,y_test)
print(score)