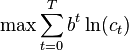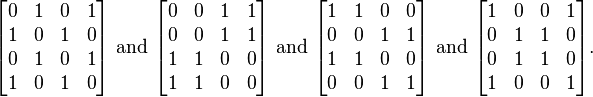动态规划
动态规划
动态规划是一种在数学、计算机科学和经济学中使用的,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。 动态规划常常适用于有重叠子问题[1]和最优子结构性质的问题,用时往往远少于朴素解法。
动态规划背后的基本思想非常简单。大致上,若要解一个给定问题,我们需要解其不同部分(即子问题),再合并子问题的解以得出原问题的解。 通常许多子问题非常相似,为此动态规划法试图仅仅解决每个子问题一次,从而减少计算量: 一旦某个给定子问题的解已经算出,则将其记忆化存储,以便下次需要同一个子问题解之时直接查表。 这种做法在重复子问题的数目关于输入的规模呈指数增长时特别有用。
目录[隐藏]
|
[编辑]概述
动态规划在查找有很多重叠子问题的情况的最优解时有效。它将问题重新组合成子问题。为了避免多次解决这些子问题,它们的结果都逐渐被计算并被保存,从简单的问题直到整个问题都被解决。因此,动态规划保存递归时的结果,因而不会在解决同样的问题时花费时间。
动态规划只能应用于有最优子结构的问题。最优子结构的意思是局部最优解能决定全局最优解(对有些问题这个要求并不能完全满足,故有时需要引入一定的近似)。简单地说,问题能够分解成子问题来解决。
[编辑]步骤
- 最优子结构性质。如果问题的最优解所包含的子问题的解也是最优的,我们就称该问题具有最优子结构性质(即满足最优化原理)。最优子结构性质为动态规划算法解决问题提供了重要线索。
- 子问题重叠性质。子问题重叠性质是指在用递归算法自顶向下对问题进行求解时,每次产生的子问题并不总是新问题,有些子问题会被重复计算多次。动态规划算法正是利用了这种子问题的重叠性质,对每一个子问题只计算一次,然后将其计算结果保存在一个表格中,当再次需要计算已经计算过的子问题时,只是在表格中简单地查看一下结果,从而获得较高的效率。
[编辑]实例
[编辑]斐波那契数列(Fibonacci polynomial)
计算斐波那契数列(Fibonacci polynomial)的一个最基础的算法是,直接按照定义计算:
function fib(n)
if n = 0 or n = 1
return 1
return fib(n − 1) + fib(n − 2)
当n=5时,fib(5)的计算过程如下:
fib(5)fib(4) + fib(3)(fib(3) + fib(2)) + (fib(2) + fib(1))((fib(2) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1))(((fib(1) + fib(0)) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1))
由上面可以看出,这种算法对于相似的子问题进行了重复的计算,因此不是一种高效的算法。实际上,该算法的运算时间是指数级增长的。 改进的方法是,我们可以通过保存已经算出的子问题的解来避免重复计算:
array map [0...n] = { 0 => 0, 1 => 1 }
fib( n )
if ( map m does not contain key n)
m[n] := fib(n − 1) + fib(n − 2)
return m[n]
将前n个已经算出的前n个数保存在数组map中,这样在后面的计算中可以直接易用前面的结果,从而避免了重复计算。算法的运算时间变为O(n)
[编辑]背包问题
背包问题作为NP完全问题,暂时不存在多项式时间算法。动态规划属于背包问题求解最优解的可行方法之一。此外,求解背包问题最优解还有搜索法等,近似解还有贪心法等,分数背包问题有最优贪心解等。 背包问题具有最优子结构和重叠子问题。动态规划一般用于求解背包问题中的整数背包问题(即每种物品所选的个数必须是整数)。 解整数背包问题: 设有n件物品,每件价值记为Pi,每件体积记为Vi,用一个最大容积为Vmax的背包,求装入物品的最大价值。 用一个数组f[i,j]表示取i件商品填充一个容积为j的背包的最大价值,显然问题的解就是f[n,Vmax].
f[i,j]=
f[i-1,j] {j=Vi}
0 {i=0 OR j=0}
对于特例01背包问题(即每件物品最多放1件,否则不放入)的问题,状态转移方程:
f[i,j]=
f[i-1,j] {j=Vi}
0 {i=0 OR j=0}
参考Pascal代码
for i:=1 to n do for j:=totv downto v[i] do f[j]:=max(f[j],f[j-v[i]]+p[i]); writeln(f[totv]);
[编辑]使用动态规划的算法
- 最长单调子序列
- 最长公共子序列
- Floyd-Warshall算法
- Viterbi算法
[编辑]参考
- ^ S. Dasgupta, C.H. Papadimitriou, and U.V. Vazirani, 'Algorithms', p 173, available athttp://www.cs.berkeley.edu/~vazirani/algorithms.html
In mathematics, computer science, and economics, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller[1] andoptimal substructure (described below). When applicable, the method takes far less time than naive methods.
The key idea behind dynamic programming is quite simple. In general, to solve a given problem, we need to solve different parts of the problem (subproblems), then combine the solutions of the subproblems to reach an overall solution. Often, many of these subproblems are really the same. The dynamic programming approach seeks to solve each subproblem only once, thus reducing the number of computations: once the solution to a given subproblem has been computed, it is stored or "memo-ized": the next time the same solution is needed, it is simply looked up. This approach is especially useful when the number of repeating subproblems grows exponentially as a function of the size of the input.
Contents[hide]
|
[edit]History
The term dynamic programming was originally used in the 1940s by Richard Bellman to describe the process of solving problems where one needs to find the best decisions one after another. By 1953, he refined this to the modern meaning, referring specifically to nesting smaller decision problems inside larger decisions,[2] and the field was thereafter recognized by the IEEE as a systems analysis and engineering topic. Bellman's contribution is remembered in the name of the Bellman equation, a central result of dynamic programming which restates an optimization problem in recursive form.
The word dynamic was chosen by Bellman to capture the time-varying aspect of the problems, and because it sounded impressive.[3] The wordprogramming referred to the use of the method to find an optimal program, in the sense of a military schedule for training or logistics. This usage is the same as that in the phrases linear programming and mathematical programming, a synonym for mathematical optimization.[4]
[edit]Overview
Dynamic programming is both a mathematical optimization method and a computer programming method. In both contexts it refers to simplifying a complicated problem by breaking it down into simpler subproblems in arecursive manner. While some decision problems cannot be taken apart this way, decisions that span several points in time do often break apart recursively; Bellman called this the "Principle of Optimality". Likewise, in computer science, a problem that can be broken down recursively is said to have optimal substructure.
If subproblems can be nested recursively inside larger problems, so that dynamic programming methods are applicable, then there is a relation between the value of the larger problem and the values of the subproblems.[5] In the optimization literature this relationship is called the Bellman equation.
[edit]Dynamic programming in mathematical optimization
In terms of mathematical optimization, dynamic programming usually refers to simplifying a decision by breaking it down into a sequence of decision steps over time. This is done by defining a sequence of value functions V1, V2, ..., Vn, with an argument y representing the state of the system at times i from 1 to n. The definition of Vn(y) is the value obtained in state y at the last time n. The values Vi at earlier timesi = n −1, n − 2, ..., 2, 1 can be found by working backwards, using a recursive relationship called the Bellman equation. For i = 2, ..., n,Vi−1 at any state y is calculated from Vi by maximizing a simple function (usually the sum) of the gain from decision i − 1 and the functionVi at the new state of the system if this decision is made. Since Vi has already been calculated for the needed states, the above operation yields Vi−1 for those states. Finally, V1 at the initial state of the system is the value of the optimal solution. The optimal values of the decision variables can be recovered, one by one, by tracking back the calculations already performed.
[edit]Dynamic programming in computer programming
There are two key attributes that a problem must have in order for dynamic programming to be applicable: optimal substructure and overlapping subproblems. However, when the overlapping problems are much smaller than the original problem, the strategy is called "divide and conquer" rather than "dynamic programming". This is why mergesort, quicksort, and finding all matches of a regular expression are not classified as dynamic programming problems.
Optimal substructure means that the solution to a given optimization problem can be obtained by the combination of optimal solutions to its subproblems. Consequently, the first step towards devising a dynamic programming solution is to check whether the problem exhibits such optimal substructure. Such optimal substructures are usually described by means of recursion. For example, given a graph G=(V,E), the shortest path p from a vertex u to a vertex v exhibits optimal substructure: take any intermediate vertex w on this shortest path p. If p is truly the shortest path, then the path p1 from u to w and p2 from w to v are indeed the shortest paths between the corresponding vertices (by the simple cut-and-paste argument described in CLRS). Hence, one can easily formulate the solution for finding shortest paths in a recursive manner, which is what the Bellman-Ford algorithm or the Floyd-Warshall algorithm does.
Overlapping subproblems means that the space of subproblems must be small, that is, any recursive algorithm solving the problem should solve the same subproblems over and over, rather than generating new subproblems. For example, consider the recursive formulation for generating the Fibonacci series: Fi = Fi−1 + Fi−2, with base case F1 = F2 = 1. Then F43 = F42 + F41, and F42 = F41 + F40. Now F41 is being solved in the recursive subtrees of both F43 as well as F42. Even though the total number of subproblems is actually small (only 43 of them), we end up solving the same problems over and over if we adopt a naive recursive solution such as this. Dynamic programming takes account of this fact and solves each subproblem only once. Note that the subproblems must be only slightly smaller (typically taken to mean a constant additive factor) than the larger problem; when they are a multiplicative factor smaller the problem is no longer classified as dynamic programming.
This can be achieved in either of two ways:[citation needed]
- Top-down approach: This is the direct fall-out of the recursive formulation of any problem. If the solution to any problem can be formulated recursively using the solution to its subproblems, and if its subproblems are overlapping, then one can easily memoize or store the solutions to the subproblems in a table. Whenever we attempt to solve a new subproblem, we first check the table to see if it is already solved. If a solution has been recorded, we can use it directly, otherwise we solve the subproblem and add its solution to the table.
- Bottom-up approach: Once we formulate the solution to a problem recursively as in terms of its subproblems, we can try reformulating the problem in a bottom-up fashion: try solving the subproblems first and use their solutions to build-on and arrive at solutions to bigger subproblems. This is also usually done in a tabular form by iteratively generating solutions to bigger and bigger subproblems by using the solutions to small subproblems. For example, if we already know the values of F41 and F40, we can directly calculate the value of F42.
Some programming languages can automatically memoize the result of a function call with a particular set of arguments, in order to speed up call-by-name evaluation (this mechanism is referred to as call-by-need). Some languages make it possible portably (e.g. Scheme, Common Lisp or Perl), some need special extensions (e.g. C++, see[6]). Some languages have automatic memoization built in, such as tabled Prolog and J, which supports memoization with the M. adverb.[7] In any case, this is only possible for a referentially transparent function.
[edit]Example: Mathematical optimization
[edit]Optimal consumption and saving
A mathematical optimization problem that is often used in teaching dynamic programming to economists (because it can be solved by hand[8]) concerns a consumer who lives over the periods ![]() and must decide how much to consume and how much to save in each period.
and must decide how much to consume and how much to save in each period.
Let ![]() be consumption in period
be consumption in period ![]() , and assume consumption yields utility
, and assume consumption yields utility ![]() as long as the consumer lives. Assume the consumer is impatient, so that he discounts future utility by a factor
as long as the consumer lives. Assume the consumer is impatient, so that he discounts future utility by a factor ![]() each period, where
each period, where ![]() . Let
. Let ![]() be capital in period
be capital in period ![]() . Assume initial capital is a given amount
. Assume initial capital is a given amount ![]() , and suppose that this period's capital and consumption determine next period's capital as
, and suppose that this period's capital and consumption determine next period's capital as ![]() , where
, where ![]() is a positive constant and
is a positive constant and ![]() . Assume capital cannot be negative. Then the consumer's decision problem can be written as follows:
. Assume capital cannot be negative. Then the consumer's decision problem can be written as follows:
Written this way, the problem looks complicated, because it involves solving for all the choice variables ![]() and
and ![]() simultaneously. (Note that
simultaneously. (Note that ![]() is not a choice variable—the consumer's initial capital is taken as given.)
is not a choice variable—the consumer's initial capital is taken as given.)
The dynamic programming approach to solving this problem involves breaking it apart into a sequence of smaller decisions. To do so, we define a sequence of value functions ![]() , for
, for ![]() which represent the value of having any amount of capital
which represent the value of having any amount of capital ![]() at each time
at each time ![]() . Note that
. Note that ![]() , that is, there is (by assumption) no utility from having capital after death.
, that is, there is (by assumption) no utility from having capital after death.
The value of any quantity of capital at any previous time can be calculated by backward induction using the Bellman equation. In this problem, for each ![]() , the Bellman equation is
, the Bellman equation is
This problem is much simpler than the one we wrote down before, because it involves only two decision variables, ![]() and
and ![]() . Intuitively, instead of choosing his whole lifetime plan at birth, the consumer can take things one step at a time. At time
. Intuitively, instead of choosing his whole lifetime plan at birth, the consumer can take things one step at a time. At time ![]() , his current capital
, his current capital ![]() is given, and he only needs to choose current consumption
is given, and he only needs to choose current consumption ![]() and saving
and saving ![]() .
.
To actually solve this problem, we work backwards. For simplicity, the current level of capital is denoted as ![]() .
. ![]() is already known, so using the Bellman equation once we can calculate
is already known, so using the Bellman equation once we can calculate ![]() , and so on until we get to
, and so on until we get to ![]() , which is the value of the initial decision problem for the whole lifetime. In other words, once we know
, which is the value of the initial decision problem for the whole lifetime. In other words, once we know ![]() , we can calculate
, we can calculate ![]() , which is the maximum of
, which is the maximum of ![]() , where
, where ![]() is the choice variable and
is the choice variable and ![]() .
.
Working backwards, it can be shown that the value function at time ![]() is
is
where each ![]() is a constant, and the optimal amount to consume at time
is a constant, and the optimal amount to consume at time ![]() is
is
which can be simplified to
We see that it is optimal to consume a larger fraction of current wealth as one gets older, finally consuming all remaining wealth in period ![]() , the last period of life.
, the last period of life.
[edit]Examples: Computer algorithms
[edit]Dijkstra's algorithm for the shortest path problem
From a dynamic programming point of view, Dijkstra's algorithm for the shortest path problem is a successive approximation scheme that solves the dynamic programming functional equation for the shortest path problem by the Reaching method.[9][10][11]
In fact, Dijkstra's explanation of the logic behind the algorithm,[12] namely
Problem 2. Find the path of minimum total length between two given nodes
and
.
We use the fact that, if
is a node on the minimal path from
to
, knowledge of the latter implies the knowledge of the minimal path from
to
.
is a paraphrasing of Bellman's famous Principle of Optimality in the context of the shortest path problem.
[edit]Fibonacci sequence
Here is a naïve implementation of a function finding the nth member of the Fibonacci sequence, based directly on the mathematical definition:
function fib(n)
if n = 0 return 0
if n = 1 return 1
return fib(n − 1) + fib(n − 2)
Notice that if we call, say, fib(5), we produce a call tree that calls the function on the same value many different times:
fib(5)fib(4) + fib(3)(fib(3) + fib(2)) + (fib(2) + fib(1))((fib(2) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1))(((fib(1) + fib(0)) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1))
In particular, fib(2) was calculated three times from scratch. In larger examples, many more values of fib, or subproblems, are recalculated, leading to an exponential time algorithm.
Now, suppose we have a simple map object, m, which maps each value of fib that has already been calculated to its result, and we modify our function to use it and update it. The resulting function requires only O(n) time instead of exponential time (but requires O(n) space):
var m := map(0 → 0, 1 → 1)
function fib(n)
if map m does not contain key n
m[n] := fib(n − 1) + fib(n − 2)
return m[n]
This technique of saving values that have already been calculated is called memoization; this is the top-down approach, since we first break the problem into subproblems and then calculate and store values.
In the bottom-up approach we calculate the smaller values of fib first, then build larger values from them. This method also uses O(n) time since it contains a loop that repeats n − 1 times, however it only takes constant (O(1)) space, in contrast to the top-down approach which requires O(n) space to store the map.
function fib(n)
if n = 0
return 0
var previousFib := 0, currentFib := 1
else repeat n − 1 times // loop is skipped if n=1
var newFib := previousFib + currentFib
previousFib := currentFib
currentFib := newFib
return currentFib
In both these examples, we only calculate fib(2) one time, and then use it to calculate both fib(4) and fib(3), instead of computing it every time either of them is evaluated.
Note that the above method actually takes ![]() time for large n because addition of two integers with
time for large n because addition of two integers with ![]() bits each takes
bits each takes ![]() time. (The nth fibonacci number has
time. (The nth fibonacci number has ![]() bits.) Also, there is a closed form for the Fibonacci sequence, known as Binet's formula, from which the
bits.) Also, there is a closed form for the Fibonacci sequence, known as Binet's formula, from which the ![]() -th term can be computed in approximately
-th term can be computed in approximately ![]() time, which is more efficient than the above dynamic programming technique. However, the simple recurrence directly gives the matrix form that leads to an approximately
time, which is more efficient than the above dynamic programming technique. However, the simple recurrence directly gives the matrix form that leads to an approximately ![]() algorithm by fast matrix exponentiation.
algorithm by fast matrix exponentiation.
[edit]A type of balanced 0–1 matrix
Consider the problem of assigning values, either zero or one, to the positions of an n × n matrix, with n even, so that each row and each column contains exactly n / 2 zeros and n / 2 ones. We ask how many different assignments there are for a given ![]() . For example, when n = 4, four possible solutions are
. For example, when n = 4, four possible solutions are
There are at least three possible approaches: brute force, backtracking, and dynamic programming.
Brute force consists of checking all assignments of zeros and ones and counting those that have balanced rows and columns (![]() zeros and
zeros and ![]() ones). As there are
ones). As there are ![]() possible assignments, this strategy is not practical except maybe up to
possible assignments, this strategy is not practical except maybe up to ![]() .
.
Backtracking for this problem consists of choosing some order of the matrix elements and recursively placing ones or zeros, while checking that in every row and column the number of elements that have not been assigned plus the number of ones or zeros are both at least n / 2. While more sophisticated than brute force, this approach will visit every solution once, making it impractical for n larger than six, since the number of solutions is already 116963796250 for n = 8, as we shall see.
Dynamic programming makes it possible to count the number of solutions without visiting them all. Imagine backtracking values for the first row – what information would we require about the remaining rows, in order to be able to accurately count the solutions obtained for each first row values? We consider k × n boards, where 1 ≤ k ≤ n, whose ![]() rows contain
rows contain ![]() zeros and
zeros and ![]() ones. The function f to whichmemoization is applied maps vectors of n pairs of integers to the number of admissible boards (solutions). There is one pair for each column and its two components indicate respectively the number of ones and zeros that have yet to be placed in that column. We seek the value of
ones. The function f to whichmemoization is applied maps vectors of n pairs of integers to the number of admissible boards (solutions). There is one pair for each column and its two components indicate respectively the number of ones and zeros that have yet to be placed in that column. We seek the value of ![]() (
(![]() arguments or one vector of
arguments or one vector of ![]() elements). The process of subproblem creation involves iterating over every one of
elements). The process of subproblem creation involves iterating over every one of ![]() possible assignments for the top row of the board, and going through every column, subtracting one from the appropriate element of the pair for that column, depending on whether the assignment for the top row contained a zero or a one at that position. If any one of the results is negative, then the assignment is invalid and does not contribute to the set of solutions (recursion stops). Otherwise, we have an assignment for the top row of the k × n board and recursively compute the number of solutions to the remaining(k − 1) × n board, adding the numbers of solutions for every admissible assignment of the top row and returning the sum, which is being memoized. The base case is the trivial subproblem, which occurs for a 1 × n board. The number of solutions for this board is either zero or one, depending on whether the vector is a permutation of n / 2
possible assignments for the top row of the board, and going through every column, subtracting one from the appropriate element of the pair for that column, depending on whether the assignment for the top row contained a zero or a one at that position. If any one of the results is negative, then the assignment is invalid and does not contribute to the set of solutions (recursion stops). Otherwise, we have an assignment for the top row of the k × n board and recursively compute the number of solutions to the remaining(k − 1) × n board, adding the numbers of solutions for every admissible assignment of the top row and returning the sum, which is being memoized. The base case is the trivial subproblem, which occurs for a 1 × n board. The number of solutions for this board is either zero or one, depending on whether the vector is a permutation of n / 2 ![]() and n / 2
and n / 2 ![]() pairs or not.
pairs or not.
For example, in the two boards shown above the sequences of vectors would be
((2, 2) (2, 2) (2, 2) (2, 2)) ((2, 2) (2, 2) (2, 2) (2, 2)) k = 4 0 1 0 1 0 0 1 1 ((1, 2) (2, 1) (1, 2) (2, 1)) ((1, 2) (1, 2) (2, 1) (2, 1)) k = 3 1 0 1 0 0 0 1 1 ((1, 1) (1, 1) (1, 1) (1, 1)) ((0, 2) (0, 2) (2, 0) (2, 0)) k = 2 0 1 0 1 1 1 0 0 ((0, 1) (1, 0) (0, 1) (1, 0)) ((0, 1) (0, 1) (1, 0) (1, 0)) k = 1 1 0 1 0 1 1 0 0 ((0, 0) (0, 0) (0, 0) (0, 0)) ((0, 0) (0, 0), (0, 0) (0, 0))
The number of solutions (sequence A058527 in OEIS) is
Links to the MAPLE implementation of the dynamic programming approach may be found among the external links.
[edit]Checkerboard
Consider a checkerboard with n × n squares and a cost-function c(i, j) which returns a cost associated with square i, j (i being the row, jbeing the column). For instance (on a 5 × 5 checkerboard),
| 5 | 6 | 7 | 4 | 7 | 8 |
|---|---|---|---|---|---|
| 4 | 7 | 6 | 1 | 1 | 4 |
| 3 | 3 | 5 | 7 | 8 | 2 |
| 2 | – | 6 | 7 | 0 | – |
| 1 | – | – | *5* | – | – |
| 1 | 2 | 3 | 4 | 5 |
Thus c(1, 3) = 5
Let us say you had a checker that could start at any square on the first rank (i.e., row) and you wanted to know the shortest path (sum of the costs of the visited squares are at a minimum) to get to the last rank, assuming the checker could move only diagonally left forward, diagonally right forward, or straight forward. That is, a checker on (1,3) can move to (2,2), (2,3) or (2,4).
| 5 | |||||
|---|---|---|---|---|---|
| 4 | |||||
| 3 | |||||
| 2 | x | x | x | ||
| 1 | o | ||||
| 1 | 2 | 3 | 4 | 5 |
This problem exhibits optimal substructure. That is, the solution to the entire problem relies on solutions to subproblems. Let us define a function q(i, j) as
- q( i, j) = the minimum cost to reach square ( i, j)
If we can find the values of this function for all the squares at rank n, we pick the minimum and follow that path backwards to get the shortest path.
Note that q(i, j) is equal to the minimum cost to get to any of the three squares below it (since those are the only squares that can reach it) plus c(i, j). For instance:
| 5 | |||||
|---|---|---|---|---|---|
| 4 | A | ||||
| 3 | B | C | D | ||
| 2 | |||||
| 1 | |||||
| 1 | 2 | 3 | 4 | 5 |
Now, let us define q(i, j) in somewhat more general terms:
The first line of this equation is there to make the recursive property simpler (when dealing with the edges, so we need only one recursion). The second line says what happens in the last rank, to provide a base case. The third line, the recursion, is the important part. It is similar to the A,B,C,D example. From this definition we can make a straightforward recursive code for q(i, j). In the following pseudocode, nis the size of the board, c(i, j) is the cost-function, and min() returns the minimum of a number of values:
function minCost(i, j)
if j < 1 or j > n
return infinity
else if i = 1
return c(i, j)
else
return min( minCost(i-1, j-1), minCost(i-1, j), minCost(i-1, j+1) ) + c(i, j)
It should be noted that this function only computes the path-cost, not the actual path. We will get to the path soon. This, like the Fibonacci-numbers example, is horribly slow since it spends mountains of time recomputing the same shortest paths over and over. However, we can compute it much faster in a bottom-up fashion if we store path-costs in a two-dimensional array q[i, j] rather than using a function. This avoids recomputation; before computing the cost of a path, we check the array q[i, j] to see if the path cost is already there.
We also need to know what the actual shortest path is. To do this, we use another array p[i, j], a predecessor array. This array implicitly stores the path to any square s by storing the previous node on the shortest path to s, i.e. the predecessor. To reconstruct the path, we lookup the predecessor of s, then the predecessor of that square, then the predecessor of that square, and so on, until we reach the starting square. Consider the following code:
function computeShortestPathArrays()
for x from 1 to n
q[1, x] := c(1, x)
for y from 1 to n
q[y, 0] := infinity
q[y, n + 1] := infinity
for y from 2 to n
for x from 1 to n
m := min(q[y-1, x-1], q[y-1, x], q[y-1, x+1])
q[y, x] := m + c(y, x)
if m = q[y-1, x-1]
p[y, x] := -1
else if m = q[y-1, x]
p[y, x] := 0
else
p[y, x] := 1
Now the rest is a simple matter of finding the minimum and printing it.
function computeShortestPath()
computeShortestPathArrays()
minIndex := 1
min := q[n, 1]
for i from 2 to n
if q[n, i] < min
minIndex := i
min := q[n, i]
printPath(n, minIndex)
function printPath(y, x)
print(x)
print("<-")
if y = 2
print(x + p[y, x])
else
printPath(y-1, x + p[y, x])
[edit]Sequence alignment
In genetics, sequence alignment is an important application where dynamic programming is essential.[3] Typically, the problem consists of transforming one sequence into another using edit operations that replace, insert, or remove an element. Each operation has an associated cost, and the goal is to find the sequence of edits with the lowest total cost.
The problem can be stated naturally as a recursion, a sequence A is optimally edited into a sequence B by either:
- inserting the first character of B, and performing an optimal alignment of A and the tail of B
- deleting the first character of A, and performing the optimal alignment of the tail of A and B
- replacing the first character of A with the first character of B, and performing optimal alignments of the tails of A and B.
The partial alignments can be tabulated in a matrix, where cell (i,j) contains the cost of the optimal alignment of A[1..i] to B[1..j]. The cost in cell (i,j) can be calculated by adding the cost of the relevant operations to the cost of its neighboring cells, and selecting the optimum.
Different variants exist, see Smith–Waterman algorithm and Needleman–Wunsch algorithm.
[edit]Tower of Hanoi puzzle
The Tower of Hanoi or Towers of Hanoi is a mathematical game or puzzle. It consists of three rods, and a number of disks of different sizes which can slide onto any rod. The puzzle starts with the disks in a neat stack in ascending order of size on one rod, the smallest at the top, thus making a conical shape.
The objective of the puzzle is to move the entire stack to another rod, obeying the following rules:
- Only one disk may be moved at a time.
- Each move consists of taking the upper disk from one of the rods and sliding it onto another rod, on top of the other disks that may already be present on that rod.
- No disk may be placed on top of a smaller disk.
The dynamic programming solution consists of solving the functional equation
- S(n,h,t) = S(n-1,h, not(h,t)) ; S(1,h,t) ; S(n-1,not(h,t),t)
where n denotes the number of disks to be moved, h denotes the home rod, t denotes the target rod, not(h,t) denotes the third rod (neither h nor t), ";" denotes concatenation, and
- S(n, h, t) := solution to a problem consisting of n disks that are to be moved from rod h to rod t.
Note that for n=1 the problem is trivial, namely S(1,h,t) = "move a disk from rod h to rod t" (there is only one disk left).
The number of moves required by this solution is 2n − 1. If the objective is to maximize the number of moves (without cycling) then the dynamic programming functional equation is slightly more complicated and 3n − 1 moves are required.[13]
[edit]Egg dropping puzzle
The following is a description of the instance of this famous puzzle involving n=2 eggs and a building with H=36 floors:[14]
-
Suppose that we wish to know which stories in a 36-story building are safe to drop eggs from, and which will cause the eggs to break on landing. We make a few assumptions:
- An egg that survives a fall can be used again.
- A broken egg must be discarded.
- The effect of a fall is the same for all eggs.
- If an egg breaks when dropped, then it would break if dropped from a higher window.
- If an egg survives a fall then it would survive a shorter fall.
- It is not ruled out that the first-floor windows break eggs, nor is it ruled out that the 36th-floor windows do not cause an egg to break.
- If only one egg is available and we wish to be sure of obtaining the right result, the experiment can be carried out in only one way. Drop the egg from the first-floor window; if it survives, drop it from the second floor window. Continue upward until it breaks. In the worst case, this method may require 36 droppings. Suppose 2 eggs are available. What is the least number of egg-droppings that is guaranteed to work in all cases?
To derive a dynamic programming functional equation for this puzzle, let the state of the dynamic programming model be a pair s = (n,k), where
- n = number of test eggs available, n = 0, 1, 2, 3, ..., N − 1.
- k = number of (consecutive) floors yet to be tested, k = 0, 1, 2, ..., H − 1.
For instance, s = (2,6) indicates that two test eggs are available and 6 (consecutive) floors are yet to be tested. The initial state of the process is s = (N,H) where N denotes the number of test eggs available at the commencement of the experiment. The process terminates either when there are no more test eggs (n = 0) or when k = 0, whichever occurs first. If termination occurs at state s = (0,k) and k > 0, then the test failed.
Now, let
- W( n, k) := minimum number of trials required to identify the value of the critical floor under the Worst Case Scenario given that the process is in state s = ( n, k).
Then it can be shown that[15]
- W( n, k) = 1 + min{max( W( n − 1, x − 1), W( n, k − x)): x in {1, 2, ..., k}}, n = 2, ..., N; k = 2, 3, 4, ..., H
with W(n,1) = 1 for all n > 0 and W(1,k) = k for all k. It is easy to solve this equation iteratively by systematically increasing the values of n and k.
An interactive online facility is available for experimentation with this model as well as with other versions of this puzzle (e.g. when the objective is to minimize the expected value of the number of trials.[15]
[edit]Algorithms that use dynamic programming
- Recurrent solutions to lattice models for protein-DNA binding
- Backward induction as a solution method for finite-horizon discrete-time dynamic optimization problems
- Method of undetermined coefficients can be used to solve the Bellman equation in infinite-horizon, discrete-time, discounted, time-invariant dynamic optimization problems
- Many string algorithms including longest common subsequence, longest increasing subsequence, longest common substring, Levenshtein distance(edit distance).
- Many algorithmic problems on graphs can be solved efficiently for graphs of bounded treewidth or bounded clique-width by using dynamic programming on a tree decomposition of the graph.
- The Cocke–Younger–Kasami (CYK) algorithm which determines whether and how a given string can be generated by a given context-free grammar
- Knuth's word wrapping algorithm that minimizes raggedness when word wrapping text
- The use of transposition tables and refutation tables in computer chess
- The Viterbi algorithm (used for hidden Markov models)
- The Earley algorithm (a type of chart parser)
- The Needleman–Wunsch and other algorithms used in bioinformatics, including sequence alignment, structural alignment, RNA structure prediction.
- Floyd's all-pairs shortest path algorithm
- Optimizing the order for chain matrix multiplication
- Pseudo-polynomial time algorithms for the subset sum and knapsack and partition problems
- The dynamic time warping algorithm for computing the global distance between two time series
- The Selinger (a.k.a. System R) algorithm for relational database query optimization
- De Boor algorithm for evaluating B-spline curves
- Duckworth–Lewis method for resolving the problem when games of cricket are interrupted
- The Value Iteration method for solving Markov decision processes
- Some graphic image edge following selection methods such as the "magnet" selection tool in Photoshop
- Some methods for solving interval scheduling problems
- Some methods for solving word wrap problems
- Some methods for solving the travelling salesman problem, either exactly (in exponential time) or approximately (e.g. via the bitonic tour)
- Recursive least squares method
- Beat tracking in music information retrieval.
- Adaptive-critic training strategy for artificial neural networks
- Stereo algorithms for solving the correspondence problem used in stereo vision.
- Seam carving (content aware image resizing)
- The Bellman–Ford algorithm for finding the shortest distance in a graph.
- Some approximate solution methods for the linear search problem.
- Kadane's algorithm for the maximum subarray problem.
[edit]See also
- Bellman equation
- Convexity in economics
- Divide and conquer algorithm
- Greedy algorithm
- Markov Decision Process
- Non-convexity (economics)
- Stochastic programming
[edit]References
- ^ S. Dasgupta, C.H. Papadimitriou, and U.V. Vazirani, 'Algorithms', p 173, available at http://www.cs.berkeley.edu/~vazirani/algorithms.html
- ^ http://www.wu-wien.ac.at/usr/h99c/h9951826/bellman_dynprog.pdf
- ^ a b Eddy, S. R., What is dynamic programming?, Nature Biotechnology, 22, 909–910 (2004).
- ^ Nocedal, J.; Wright, S. J.: Numerical Optimization, page 9, Springer, 2006..
- ^ Cormen, T. H.; Leiserson, C. E.; Rivest, R. L.; Stein, C. (2001), Introduction to Algorithms (2nd ed.), MIT Press & McGraw–Hill, ISBN 0-262-03293-7 . pp. 327–8.
- ^ http://www.apl.jhu.edu/~paulmac/c++-memoization.html
- ^ "M. Memo". J Vocabulary. J Software. Retrieved 28 October 2011.
- ^ Stokey et al., 1989, Chap. 1
- ^ Sniedovich, M. (2006), "Dijkstra’s algorithm revisited: the dynamic programming connexion" (PDF), Journal of Control and Cybernetics 35 (3): 599–620.Online version of the paper with interactive computational modules.
- ^ Denardo, E.V. (2003), Dynamic Programming: Models and Applications, Mineola, NY: Dover Publications, ISBN 978-0-486-42810-9
- ^ Sniedovich, M. (2010), Dynamic Programming: Foundations and Principles, Taylor & Francis, ISBN 978-0-8247-4099-3
- ^ Dijkstra 1959, p. 270
- ^ Moshe Sniedovich (2002), "OR/MS Games: 2. The Towers of Hanoi Problem,", INFORMS Transactions on Education 3(1): 34–51.
- ^ Konhauser J.D.E., Velleman, D., and Wagon, S. (1996). Which way did the Bicycle Go? Dolciani Mathematical Expositions – No 18. The Mathematical Association of America.
- ^ a b Sniedovich, M. (2003). The joy of egg-dropping in Braunschweig and Hong Kong. INFORMS Transactions on Education, 4(1) 48–64.
[edit]Further reading
- Adda, Jerome; Cooper, Russell (2003), Dynamic Economics, MIT Press. An accessible introduction to dynamic programming in economics. The link contains sample programs.
- Bellman, Richard (1954), "The theory of dynamic programming", Bulletin of the American Mathematical Society 60: 503–516,doi:10.1090/S0002-9904-1954-09848-8, MR 0067459. Includes an extensive bibliography of the literature in the area, up to the year 1954.
- Bellman, Richard (1957), Dynamic Programming, Princeton University Press. Dover paperback edition (2003), ISBN 0-486-42809-5.
- Bertsekas, D. P. (2000), Dynamic Programming and Optimal Control (2nd ed.), Athena Scientific, ISBN 1-886529-09-4. In two volumes.
- Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001), Introduction to Algorithms (2nd ed.), MIT Press & McGraw-Hill, ISBN 0-262-03293-7. Especially pp. 323–69.
- Dreyfus, Stuart E.; Law, Averill M. (1977), The art and theory of dynamic programming, Academic Press, ISBN 978-0-12-221860-6.
- Giegerich, R.; Meyer, C.; Steffen, P. (2004), "A Discipline of Dynamic Programming over Sequence Data", Science of Computer Programming51 (3): 215–263, doi:10.1016/j.scico.2003.12.005.
- Meyn, Sean (2007), Control Techniques for Complex Networks, Cambridge University Press, ISBN 978-0-521-88441-9.
- S. S. Sritharan, "Dynamic Programming of the Navier-Stokes Equations," in Systems and Control Letters, Vol. 16, No. 4, 1991, pp. 299–307.
- Stokey, Nancy; Lucas, Robert E.; Prescott, Edward (1989), Recursive Methods in Economic Dynamics, Harvard Univ. Press, ISBN 978-0-674-75096-8.
|
||||||||||||||||||||||||||||||||||||||||||||||
[edit]External links
- An Introduction to Dynamic Programming
- Dyna, a declarative programming language for dynamic programming algorithms
- Wagner, David B., 1995, "Dynamic Programming." An introductory article on dynamic programming in Mathematica.
- Ohio State University: CIS 680: class notes on dynamic programming, by Eitan M. Gurari
- A Tutorial on Dynamic programming
- MIT course on algorithms – Includes a video lecture on DP along with lecture notes
- More DP Notes
- King, Ian, 2002 (1987), "A Simple Introduction to Dynamic Programming in Macroeconomic Models." An introduction to dynamic programming as an important tool in economic theory.
- Dynamic Programming: from novice to advanced A TopCoder.com article by Dumitru on Dynamic Programming
- Algebraic Dynamic Programming – a formalized framework for dynamic programming, including an entry-level course to DP, University of Bielefeld
- Dreyfus, Stuart, "Richard Bellman on the birth of Dynamic Programming."
- Dynamic programming tutorial
- A Gentle Introduction to Dynamic Programming and the Viterbi Algorithm
- Tabled Prolog BProlog and XSB
- Online interactive dynamic programming modules including, shortest path, traveling salesman, knapsack, false coin, egg dropping, bridge and torch, replacement, chained matrix products, and critical path problem.