面试必备:高频算法题汇总「图文解析 + 教学视频 + 范例代码」之 字符串处理+动态规划 合集!
Attention
秋招接近尾声,我总结了 牛客、WanAndroid 上,有关笔试面经的帖子中出现的算法题,结合往年考题写了这一系列文章,所有文章均与 LeetCode 进行核对、测试。欢迎食用
本文将覆盖 「字符串处理」 + 「动态规划」 方面的面试算法题,文中我将给出:
- 面试中的题目
- 解题的思路
- 特定问题的技巧和注意事项
- 考察的知识点及其概念
- 详细的代码和解析
开始之前,我们先看下会有哪些重点案例:
为了方便大家跟进学习,我在 GitHub 建立了一个仓库
仓库地址:超级干货!精心归纳视频、归类、总结,各位路过的老铁支持一下!给个 Star !
现在就让我们开始吧!
字符串处理
字符串广泛应用 在 Java 编程中,在 Java 中字符串属于对象,Java 提供了 String 类来创建和操作字符串。面试中的字符串处理问题,主要是对于字符串各种方法的灵活应用。下面结合实例,讲讲常见的考点:
括号生成
给定 n,表示有 n 对括号, 请写一个函数以将其生成所有的括号组合,并返回组合结果。
例如
给出 n = 3,生成结果为:
[
"((()))",
"(()())",
"(())()",
"()(())",
"()()()"
]
解题思路
使用 回溯法
只有在我们知道序列仍然保持有效时才添加 ‘(’ or ‘)’,而不是像 方法一 那样每次添加。我们可以通过跟踪到目前为止放置的左括号和右括号的数目来做到这一点,
如果我们还剩一个位置,我们可以开始放一个左括号。 如果它不超过左括号的数量,我们可以放一个右括号。
视频
视频讲解和源码-生成括号
public List<String> generateParenthesis(int n) {
List<String> res = new ArrayList<>();
helper(n, n, "", res);
return res;
}
// DFS
private void helper(int nL, int nR, String parenthesis, List<String> res) {
// nL 和 nR 分别代表左右括号剩余的数量
if (nL < 0 || nR < 0) {
return;
}
if (nL == 0 && nR == 0) {
res.add(parenthesis);
return;
}
helper(nL - 1, nR, parenthesis + "(", res);
if (nL >= nR) {
return;
}
helper(nL, nR - 1, parenthesis + ")", res);
}
复杂度
Excel表列标题
给定一个正整数,返回相应的列标题,如Excel表中所示。如:
1 -> A,
2 -> B
…
26 -> Z,
27 -> AA
示例 :
输入: 28
输出: "AB"
解题思路
- 网上看了 n 多人的方法,感觉很多都做麻烦了。大多数人都困在这个 ‘A’ 或者说 n = 0 上
- 举个例子,如果输入 26,我们一般会直接把它 %26 这样得到的就是一个 0
- 然而很多人得到字符的方式都是 %26 + 64,也就是 0 + ‘A’ = ‘A’ ,正确答案当然是 ‘Z’,于是加了一堆判断
- 其实不用那么麻烦,一个 n-- 就能搞定.
public String convertToTitle (int n) {
StringBuilder str = new StringBuilder();
while (n > 0) {
n--;
str.append ( (char) ( (n % 26) + 'A'));
n /= 26;
}
return str.reverse().toString();
}
翻转游戏
给定一个只包含两种字符的字符串:+和-,你和你的小伙伴轮流翻转"++“变成”–"。当一个人无法采取行动时游戏结束,另一个人将是赢家。编写一个函数,计算字符串在一次有效移动后的所有可能状态。
示例 :
输入:s = "++++"
[
"--++",
"+--+",
"++--"
]
解题思路
- 我们从第二个字母开始遍历
- 每次判断当前字母是否为+,和之前那个字母是否为+
- 如果都为加,则将翻转后的字符串存入结果中即可
public List<String> generatePossibleNextMoves (String s) {
List list = new ArrayList();
// indexOf 方法使用 看下方拓展
for (int i = -1; (i = s.indexOf ("++", i + 1)) >= 0;) {
list.add (s.substring (0, i) + "--" + s.substring (i + 2));
}
return list;
}
拓展:
Java中字符串中子串的查找共有四种方法,如下:
- int indexOf(String str) :返回第一次出现的指定子字符串在此字符串中的索引。
- int indexOf(String str, int startIndex):从指定的索引处开始,返回第一次出现的指定子字符串在此字符串中的索引。
- int lastIndexOf(String str) :返回在此字符串中最右边出现的指定子字符串的索引。
- int lastIndexOf(String str, int startIndex) :从指定的索引处开始向后搜索,返回在此字符串中最后一次出现的指定子字符串的索引。
substring() 方法返回字符串的子字符串。
- public String substring(int beginIndex) 返回 beginIndex 后的字符串
- public String substring(int beginIndex, int endIndex) 返回 beginIndex 到 endIndex 之间的字符串
翻转字符串中的单词
给定一个字符串,逐个翻转字符串中的每个单词。
示例 :
输入: "a good example"
输出: "example good a"
解释: 如果两个单词间有多余的空格,将反转后单词间的空格减少到只含一个。
解题思路
- 通过 split 方法,以 “ ” 为标识符为基准拆分字符串
- 将拆分后的字符串倒序插入数组中即可
public String reverseWords(String s) {
if(s.length() == 0 || s == null){
return " ";
}
//按照空格将s切分
String[] array = s.split(" ");
StringBuilder sb = new StringBuilder();
//从后往前遍历array,在sb中插入单词
for(int i = array.length - 1; i >= 0; i--){
if(!array[i].equals("")) {
// 为防止字符串首多一个 “ ” 判断当前是不是空字符串
// 是字符串第一个就不输出空格
if (sb.length() > 0) {
sb.append(" ");
}
sb.append(array[i]);
}
}
return sb.toString();
}
字符串转换整数 (atoi)
实现atoi这个函数,将一个字符串转换为整数。如果没有合法的整数,返回0。如果整数超出了32位整数的范围,返回 INT_MAX(2147483647) 如果是正整数,或者 INT_MIN(-2147483648) 如果是负整数。
示例 :
输入: "4193 with words"
输出: 4193
解释: 转换截止于数字 '3' ,因为它的下一个字符不为数字。
示例 4:
输入: "words and 987"
输出: 0
解释: 第一个非空字符是 'w', 但它不是数字或正、负号。
因此无法执行有效的转换。
解题思路
- 首先我们要知道该数正负
- 根据题意调用 trim() 去掉空格
- 去完多余空格之后,首位有三种情况 ‘+’ ‘-’ 其他
- 设一个 falg 叫做 sign 默认值为一,如果监测到 ‘-’ 则设为 -1
- 这样一来后面求出的结果乘以 sigh 就能带上正负值
- 在定义一个 num 值用于保存答案数值
- for 循环从头到尾访问字符串
- 先判断当前位是否为数字,这时分两种情况
- 如果字符串首位就不是数字和 -+ 号,根据题意直接退出循环
- 如果为数字就将 sum 的值 *10 倍,再将其加入 sum 中
- 如果值超过 MAX_VALUE 跳出循环
- 对应 *sigh 输出正负值,或者 MAX_VALUE 或 MIN_VALUE 即可
视频
视频讲解和源码-字符串转换整数
public int myAtoi(String str) {
if(str == null) {
return 0;
}
str = str.trim();
if (str.length() == 0) {
return 0;
}
int sign = 1;
int index = 0;
if (str.charAt(index) == '+') {
index++;
} else if (str.charAt(index) == '-') {
sign = -1;
index++;
}
long num = 0;
for (; index < str.length(); index++) {
if (str.charAt(index) < '0' || str.charAt(index) > '9') {
break;
}
num = num * 10 + (str.charAt(index) - '0');
if (num > Integer.MAX_VALUE ) {
break;
}
}
if (num * sign >= Integer.MAX_VALUE) {
return Integer.MAX_VALUE;
}
if (num * sign <= Integer.MIN_VALUE) {
return Integer.MIN_VALUE;
}
return (int)num * sign;
}
注:trim() 函数是去掉String字符串的首尾空格;
最长公共前缀
编写一个函数来查找字符串数组中的最长公共前缀。
如果不存在公共前缀,返回空字符串 “”。
示例 :
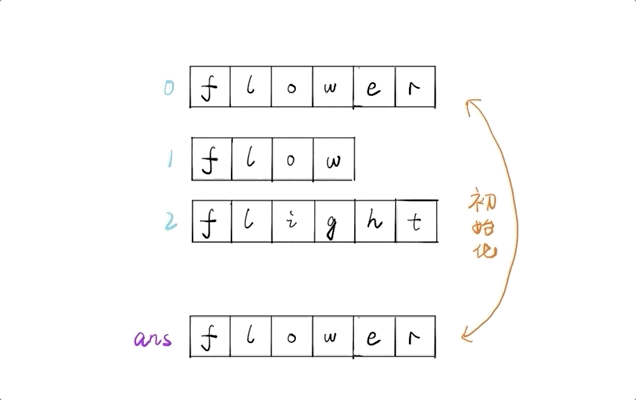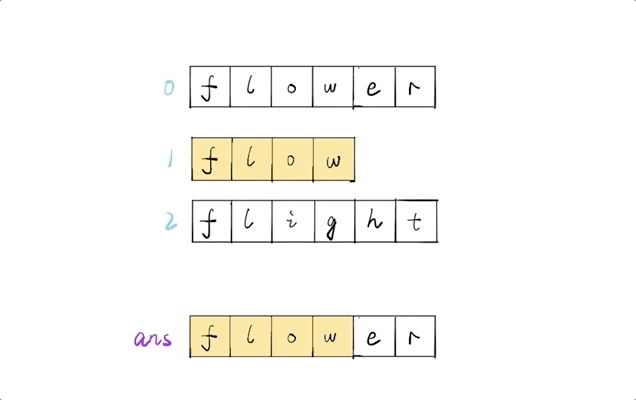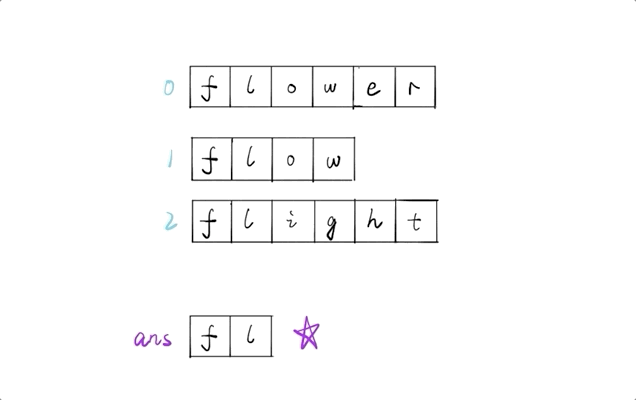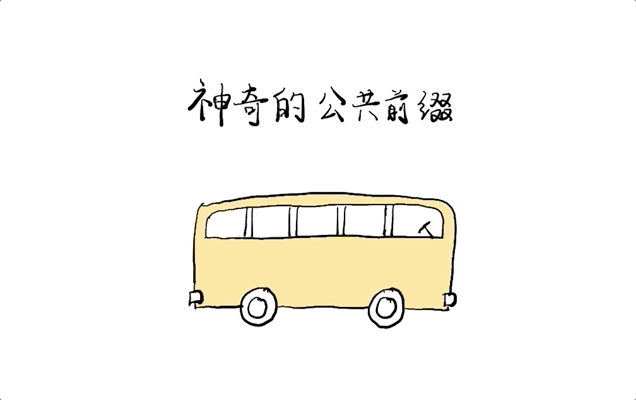
输入: ["flower","flow","flight"]
输出: "fl"
解题思路
标签:链表
当字符串数组长度为 0 时则公共前缀为空,直接返回
令最长公共前缀 ans 的值为第一个字符串,进行初始化
遍历后面的字符串,依次将其与 ans 进行比较,两两找出公共前缀,最终结果即为最长公共前缀
如果查找过程中出现了 ans 为空的情况,则公共前缀不存在直接返回
s 为所有字符串的长度之和
视频
最长公共前缀
public String longestCommonPrefix(String[] strs) {
if (strs == null || strs.length == 0) {
return "";
}
String prefix = strs[0];
for(int i = 1; i < strs.length; i++) {
int j = 0;
while (j < strs[i].length() && j < prefix.length() && strs[i].charAt(j) == prefix.charAt(j)) {
j++;
}
if( j == 0) {
return "";
}
prefix = prefix.substring(0, j);
}
return prefix;
}
时间复杂度:
O ( s ) O(s) O(s)
回文数
判断一个正整数是不是回文数。回文数的定义是,将这个数反转之后,得到的数仍然是同一个数。
示例 :
输入: 121
输出: true
解题思路
通过取整和取余操作获取整数中对应的数字进行比较。
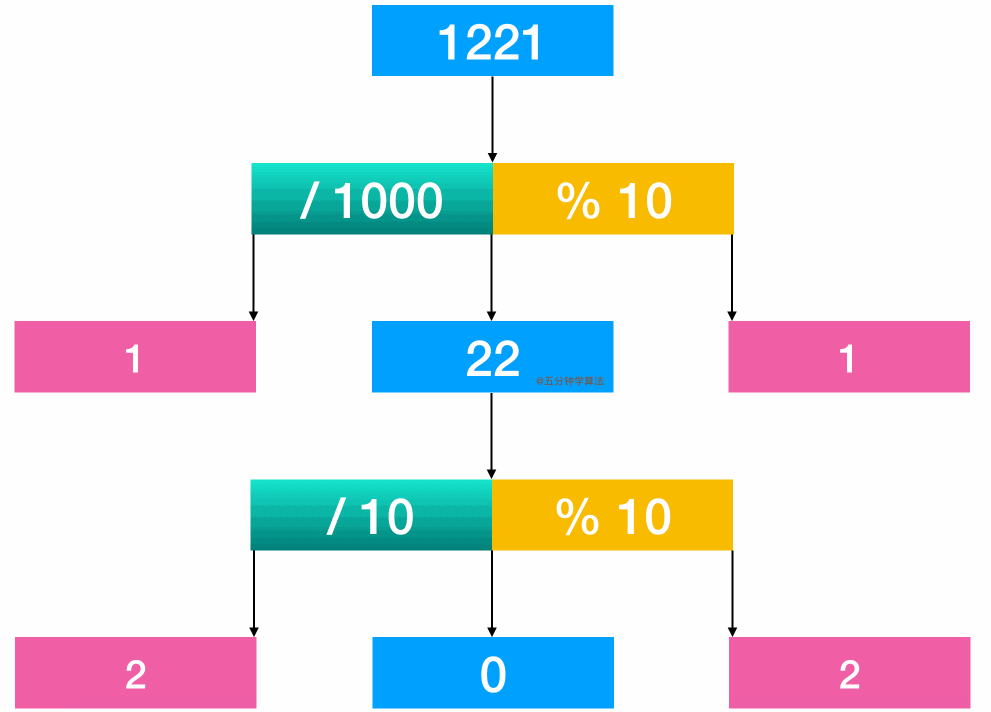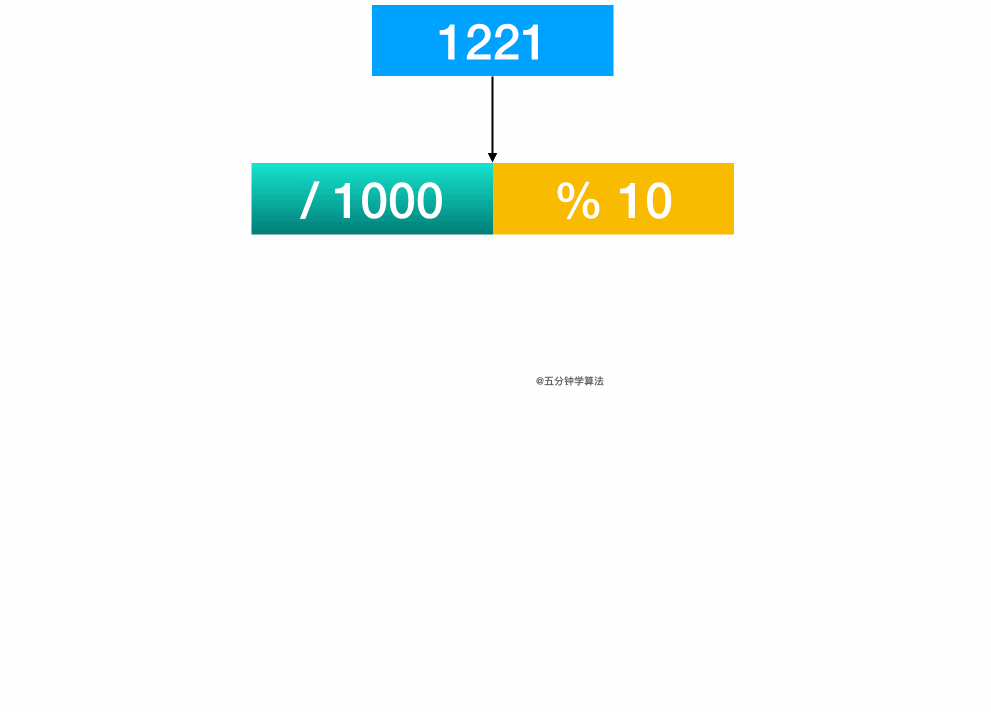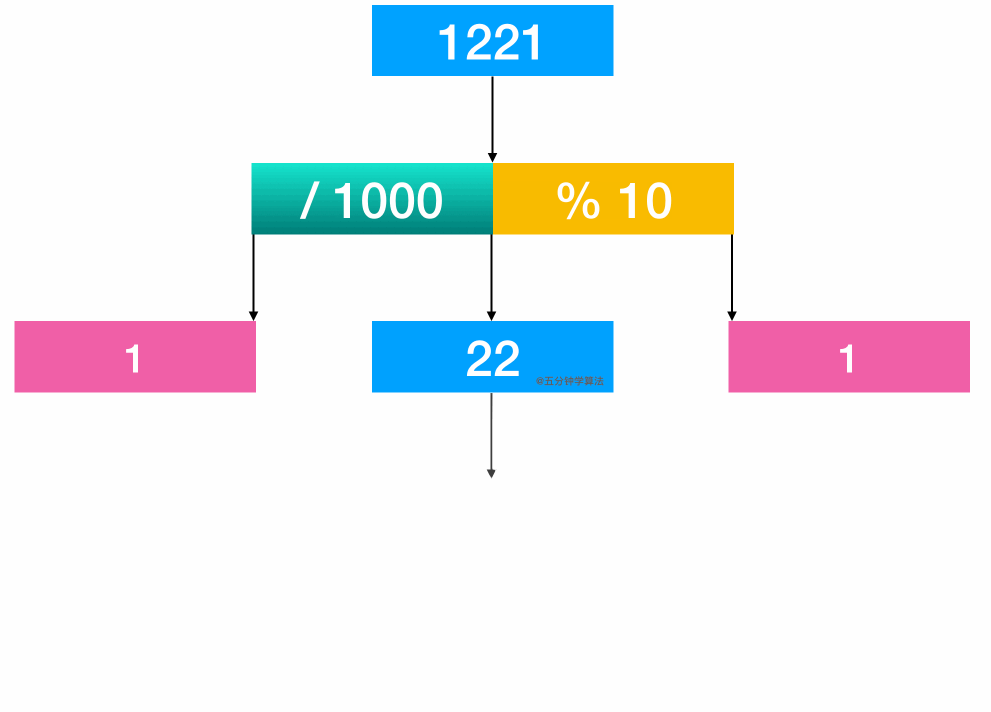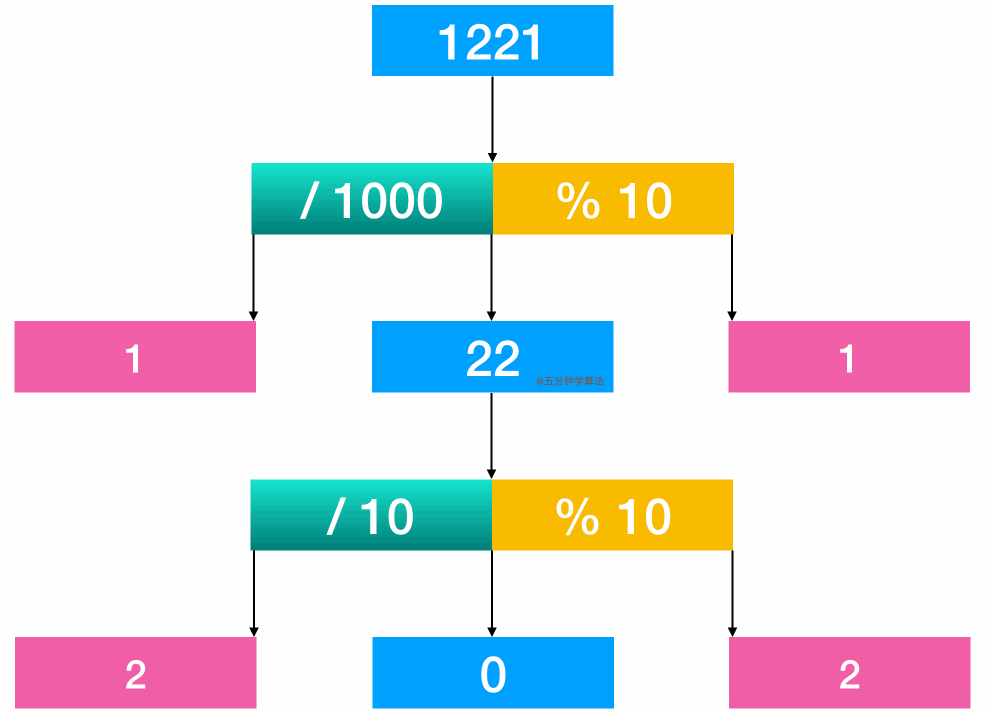
举个例子:1221 这个数字。
通过计算 1221 / 1000, 得首位1
通过计算 1221 % 10, 可得末位 1
进行比较
再将 22 取出来继续比较
视频
回文数
public boolean palindromeNumber(int num) {
// Write your code here
if(num < 0){
return false;
}
int div = 1;
while(num / div >= 10){
div *= 10;
}
while(num > 0){
if(num / div != num % 10){
return false;
}
num = (num % div) / 10;
div /= 100;
}
return true;
}
动态规划
动态规划常常适用于有重叠子问题和最优子结构性质的问题,动态规划方法所耗时间往往远少于朴素解法。其背后的基本思想非常简单。大致上,若要解一个给定问题,我们需要解其不同部分(即子问题),再根据子问题的解以得出原问题的解。
通常许多子问题非常相似,为此动态规划法试图仅仅解决每个子问题一次,从而减少计算量:一旦某个给定子问题的解已经算出,则将其记忆化存储,以便下次需要同一个子问题解之时直接查表。这种做法在重复子问题的数目关于输入的规模呈指數增長时特别有用。
单词拆分
给定字符串 s 和单词字典 dict,确定 s 是否可以分成一个或多个以空格分隔的子串,并且这些子串都在字典中存在。
示例 :
输入: s = "applepenapple", wordDict = ["apple", "pen"]
输出: true
解释: 返回 true 因为 "applepenapple" 可以被拆分成 "apple pen apple"。
注意你可以重复使用字典中的单词。
解题思路
这个方法的想法是对于给定的字符串 s 可以被拆分成子问题 s1 和 s2 。如果这些子问题都可以独立地被拆分成符合要求的子问题,那么整个问题 s 也可以满足。也就是,如果 c a t s a n d d o g catsanddog catsanddog 可以拆分成两个子字符串 “ c a t s a n d catsand catsand” 和 “ d o g dog dog” 。子问题 “ c a t s a n d catsand catsand” 可以进一步拆分成 “ c a t s cats cats” 和 “ a n d and and” ,这两个独立的部分都是字典的一部分,所以 “ c a t s a n d catsand catsand” 满足题意条件,再往前, “ c a t s a n d catsand catsand” 和 “ d o g dog dog” 也分别满足条件,所以整个字符串 “ c a t s a n d d o g catsanddog catsanddog” 也满足条件。
现在,我们考虑 d p dp dp 数组求解的过程:
- 我们使用 n + 1 n+1 n+1 大小数组的 d p dp dp ,其中 n n n 是给定字符串的长度。
- 我们也使用 2 个下标指针 i i i 和 j j j ,其中 i i i 是当前字符串从头开始的子字符串 ( s ′ ) (s') (s′)的长度, j j j 是当前子字符串 ( s ′ ) (s') (s′)的拆分位置,拆分成 s ′ ( 0 , j ) s'(0,j) s′(0,j)和 s ′ ( j + 1 , i ) s'(j+1,i) s′(j+1,i)。
- 为了求出 d p dp dp 数组,我们初始化 d p [ 0 ] dp[0] dp[0] 为 t r u e true true ,这是因为空字符串总是字典的一部分。 d p dp dp 数组剩余的元素都初始化为 f a l s e false false 。
- 我们用下标 i i i 来考虑所有从当前字符串开始的可能的子字符串。对于每一个子字符串,我们通过下标 j j j 将它拆分成
s1'和s2'(注意i现在指向s2'的结尾)。 - 为了将 d p [ i ] dp[i] dp[i] 数组求出来,我们依次检查每个 d p [ j ] dp[j] dp[j] 是否为 t r u e true true ,也就是子字符串
s1′是否满足题目要求。如果满足,我们接下来检查s2′是否在字典中。如果包含,我们接下来检查s2′是否在字典中,如果两个字符串都满足要求,我们让 d p [ i ] dp[i] dp[i] 为 t r u e true true ,否则令其为 f a l s e false false 。
public boolean wordBreak(String s, List<String> wordDict) {
Set<String> wordDictSet=new HashSet(wordDict);
boolean[] dp = new boolean[s.length() + 1];
dp[0] = true;
for (int i = 1; i <= s.length(); i++) {
for (int j = 0; j < i; j++) {
if (dp[j] && wordDictSet.contains(s.substring(j, i))) {
dp[i] = true;
break;
}
}
}
return dp[s.length()];
}
复杂度分析
时间复杂度: O ( n 2 ) O(n^2) O(n2) 。求出 d p dp dp 数组需要两重循环。
空间复杂度: O ( n ) O(n) O(n)。 d p dp dp 数组的长度是 n + 1 n+1 n+1。
爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
示例 :
输入: 3
输出: 3
解释: 有三种方法可以爬到楼顶。
1 阶 + 1 阶 + 1 阶
1 阶 + 2 阶
2 阶 + 1 阶
解题思路
感觉这题类似斐波那契数列。不难发现,这个问题可以被分解为一些包含最优子结构的子问题,即它的最优解可以从其子问题的最优解来有效地构建,我们可以使用动态规划来解决这一问题。
第 i i i 阶可以由以下两种方法得到:
在第 ( i − 1 ) (i−1) (i−1) 阶后向上爬 1 阶。
在第 ( i − 2 ) (i−2) (i−2) 阶后向上爬 2 阶。
所以到达第 i i i 阶的方法总数就是到第 ( i − 1 ) (i−1) (i−1) 阶和第 ( i − 2 ) (i−2) (i−2) 阶的方法数之和。
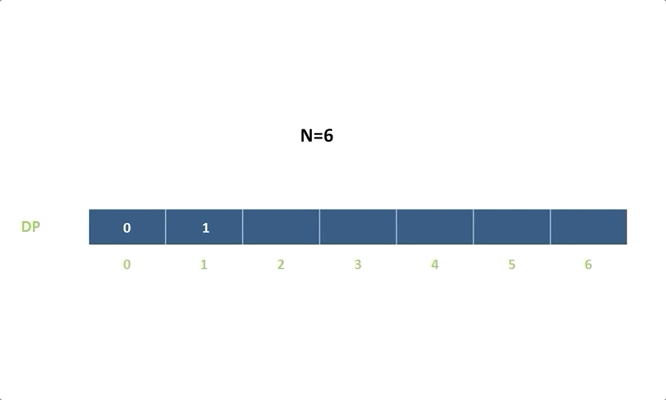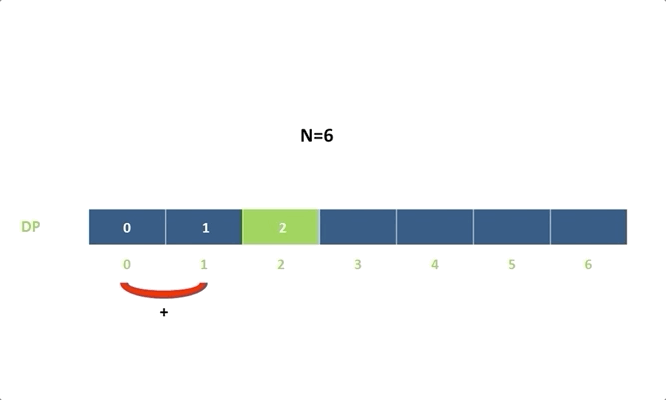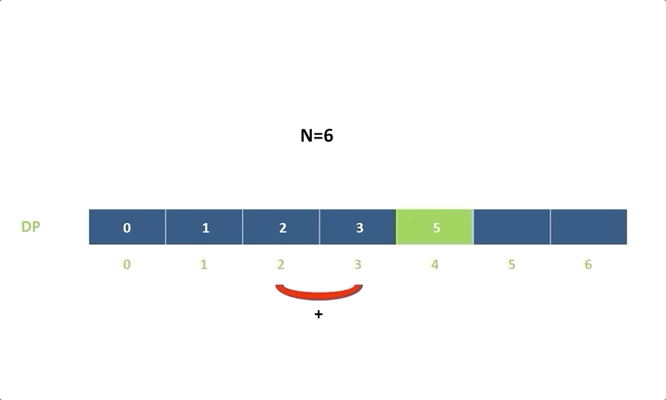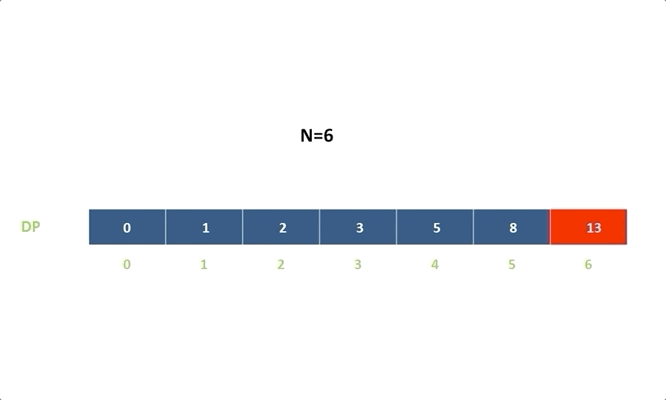
令 d p [ i ] dp[i] dp[i] 表示能到达第 i i i 阶的方法总数:
d p [ i ] = d p [ i − 1 ] + d p [ i − 2 ] dp[i]=dp[i-1]+dp[i-2] dp[i]=dp[i−1]+dp[i−2]
d p [ i ] = d p [ i − 1 ] + d p [ i − 2 ] dp[i]=dp[i−1]+dp[i−2] dp[i]=dp[i−1]+dp[i−2]
public int climbStairs(int n) {
if (n == 0) return 0;
int[] array = new int[n + 1];
array[0] = 1;
if (array.length > 1) {
array[1] = 1;
}
for(int i = 2; i < array.length; i++) {
array[i] = array[i - 1] + array[i - 2];
}
return array[n];
}
打家劫舍
假设你是一个专业的窃贼,准备沿着一条街打劫房屋。每个房子都存放着特定金额的钱。你面临的唯一约束条件是:相邻的房子装着相互联系的防盗系统,且 当相邻的两个房子同一天被打劫时,该系统会自动报警。给定一个非负整数列表,表示每个房子中存放的钱, 算一算,如果今晚去打劫,在不触动报警装置的情况下, 你最多可以得到多少钱 。
示例 :
输入: [2,7,9,3,1]
输出: 12
解释: 偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。
解题思路
考虑所有可能的抢劫方案过于困难。一个自然而然的想法是首先从最简单的情况开始。记:
f ( k ) = f(k) = f(k)= 从前
k个房屋中能抢劫到的最大数额, A i A_i Ai = 第i个房屋的钱数。
首先看 n = 1 的情况,显然 f(1) = A 1 A_1 A1 。
再看 n = 2, f ( 2 ) = m a x ( A 1 , A 2 ) f(2) = max(A_1 , A_2 ) f(2)=max(A1,A2)。
对于 n = 3,有两个选项:
抢第三个房子,将数额与第一个房子相加。
不抢第三个房子,保持现有最大数额。
显然,你想选择数额更大的选项。于是,可以总结出公式:
f ( k ) = m a x ( f ( k – 2 ) + A k , f ( k – 1 ) ) f(k) = max(f(k – 2) + A_k , f(k – 1)) f(k)=max(f(k–2)+Ak,f(k–1))
我们选择 f ( – 1 ) = f ( 0 ) = 0 f(–1) = f(0) = 0 f(–1)=f(0)=0 为初始情况,这将极大地简化代码。
答案为 f ( n ) f(n) f(n)。可以用一个数组来存储并计算结果。不过由于每一步你只需要前两个最大值,两个变量就足够用了。
public long houseRobber(int[] A) {
if (A.length == 0) return 0;
long[] res = new long[A.length + 1];
res[0] = 0;
res[1] = A[0];
for (int i = 2; i < res.length; i++) {
res[i] = Math.max(res[i - 2] + A[i - 1], res[i - 1]);
}
return res[A.length];
}
复杂度分析
时间复杂度: O ( n ) O(n) O(n)。其中 n 为房子的数量。
空间复杂度: O ( 1 ) O(1) O(1)。
编辑距离
给出两个单词word1和word2,计算出将 word1 转换为word2的最少操作次数。你总共三种操作方法:插入一个字符、删除一个字符、替换一个字符。
示例 :
输入: word1 = "horse", word2 = "ros"
输出: 3
解释:
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')
输入: word1 = "intention", word2 = "execution"
输出: 5
解释:
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')
解题思路
我们的目的是让问题简单化,比如说两个单词 horse 和 ros 计算他们之间的编辑距离 D,容易发现,如果把单词变短会让这个问题变得简单,很自然的想到用 D[n][m] 表示输入单词长度为 n 和 m 的编辑距离。
具体来说,D[i][j] 表示 word1 的前 i 个字母和 word2 的前 j 个字母之间的编辑距离。
当我们获得 D[i-1][j],D[i][j-1] 和 D[i-1][j-1] 的值之后就可以计算出 D[i][j]。
每次只可以往单个或者两个字符串中插入一个字符
那么递推公式很显然了
如果两个子串的最后一个字母相同,word1[i] = word2[i] 的情况下:
D [ i ] [ j ] = 1 + min ( D [ i − 1 ] [ j ] , D [ i ] [ j − 1 ] , D [ i − 1 ] [ j − 1 ] − 1 ) D[i][j] = 1 + \min(D[i - 1][j], D[i][j - 1], D[i - 1][j - 1] - 1) D[i][j]=1+min(D[i−1][j],D[i][j−1],D[i−1][j−1]−1)
D [ i ] [ j ] = 1 + m i n ( D [ i − 1 ] [ j ] , D [ i ] [ j − 1 ] , D [ i − 1 ] [ j − 1 ] − 1 ) D[i][j]=1+min(D[i−1][j],D[i][j−1],D[i−1][j−1]−1) D[i][j]=1+min(D[i−1][j],D[i][j−1],D[i−1][j−1]−1)
否则,word1[i] != word2[i] 我们将考虑替换最后一个字符使得他们相同:
D [ i ] [ j ] = 1 + min ( D [ i − 1 ] [ j ] , D [ i ] [ j − 1 ] , D [ i − 1 ] [ j − 1 ] ) D[i][j] = 1 + \min(D[i - 1][j], D[i][j - 1], D[i - 1][j - 1]) D[i][j]=1+min(D[i−1][j],D[i][j−1],D[i−1][j−1])
D [ i ] [ j ] = 1 + m i n ( D [ i − 1 ] [ j ] , D [ i ] [ j − 1 ] , D [ i − 1 ] [ j − 1 ] ) D[i][j]=1+min(D[i−1][j],D[i][j−1],D[i−1][j−1]) D[i][j]=1+min(D[i−1][j],D[i][j−1],D[i−1][j−1])
所以每一步结果都将基于上一步的计算结果,示意如下:
同时,对于边界情况,一个空串和一个非空串的编辑距离为 D[i][0] = i 和 D[0][j] = j。
综上我们得到了算法的全部流程。
温馨提示,如果思维不好理解的话,把解题思路记清楚就行
public int minDistance(String word1, String word2) {
// write your code here
int n = word1.length();
int m = word2.length();
int[][] dp = new int[n + 1][m + 1];
for (int i = 0; i < n + 1; i++){
dp[i][0] = i;
}
for (int j = 0; j < m + 1; j++){
dp[0][j] = j;
}
for (int i = 1; i< n + 1; i++){
for (int j = 1; j < m + 1; j++){
if (word1.charAt(i - 1) == word2.charAt(j - 1)){
dp[i][j] = dp[i - 1][j - 1];
} else {
dp[i][j] = 1 + Math.min(dp[i - 1][j - 1], Math.min(dp[i][j - 1], dp[i - 1][j]));
}
}
}
return dp[n][m];
}
复杂度分析
时间复杂度 : O ( m n ) O(m n) O(mn),两层循环显而易见。
空间复杂度 : O ( m n ) O(m n) O(mn),循环的每一步都要记录结果。
乘积最大子序列
给定一个整数数组 nums ,找出一个序列中乘积最大的连续子序列(该序列至少包含一个数)。
示例 :
输入: [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
解题思路
- 遍历数组时计算当前最大值,不断更新
- 令imax为当前最大值,则当前最大值为
imax = max(imax * nums[i], nums[i]) - 由于存在负数,那么会导致最大的变最小的,最小的变最大的。因此还需要维护当前最小值
imin,imin = min(imin * nums[i], nums[i]) - 当负数出现时则imax与imin进行交换再进行下一步计算
public int maxProduct(int[] nums) {
int max = Integer.MIN_VALUE, imax = 1, imin = 1;
for(int i=0; i<nums.length; i++){
if(nums[i] < 0){
int tmp = imax;
imax = imin;
imin = tmp;
}
imax = Math.max(imax*nums[i], nums[i]);
imin = Math.min(imin*nums[i], nums[i]);
max = Math.max(max, imax);
}
return max;
}
时间复杂度:
- O(n)
Attention
- 为了提高文章质量,防止冗长乏味
下一部分算法题
-
本片文章篇幅总结越长。我一直觉得,一片过长的文章,就像一堂超长的 会议/课堂,体验很不好,所以我打算再开一篇文章
-
在后续文章中,我将继续针对
链表栈队列堆动态规划矩阵位运算等近百种,面试高频算法题,及其图文解析 + 教学视频 + 范例代码,进行深入剖析有兴趣可以继续关注 _yuanhao 的编程世界 -
不求快,只求优质,每篇文章将以 2 ~ 3 天的周期进行更新,力求保持高质量输出
相关文章
「面试高频」二叉搜索树+双指针+贪心 算法题指北
面试必备:高频算法题汇总「图文解析 + 教学视频 + 范例代码」之 二分 + 哈希表 + 堆 + 优先队列 部分!
面试必备:高频算法题汇总「图文解析 + 教学视频 + 范例代码」必问之 链表 + 栈 + 队列 部分!
? 面试必备:高频算法题汇总「图文解析 + 教学视频 + 范例代码」必问之 排序 + 二叉树 部分!?
高效解决「SQLite」数据库并发访问安全问题,只这一篇就够了
每个人都要学的图片压缩终极奥义,有效解决 Android 程序 OOM
Android 让你的 Room 搭上 RxJava 的顺风车 从重复的代码中解脱出来
ViewModel 和 ViewModelProvider.Factory:ViewModel 的创建者
单例模式-全局可用的 context 对象,这一篇就够了
缩放手势 ScaleGestureDetector 源码解析,这一篇就够了
请点赞!因为你的鼓励是我写作的最大动力!
为了方便大家跟进学习,我在 GitHub 建立了一个仓库
仓库地址:超级干货!精心归纳视频、归类、总结,各位路过的老铁支持一下!给个 Star !