必须了解的编程基础 -- 回溯法：以0/1背包问题为例

DP解法见之前的博客动态规划 – 从Fibonacci数列到0/1背包问题

1. 内容

• 回溯法解题步骤；
• 使用回溯法解决0/1背包问题，并在参考文献[1]上进行验证。

2. 回溯法解题步骤

（1）定义解空间；
（2）组织解空间为树或图，使其便于搜索；
（3）按照深度优先方法搜索解空间。

3. 回溯法解决0/1背包问题

以三个物品对象为例，按照第2小节中的步骤，进行问题解决。

3.1 定义解空间

以三个物品对象为例，设解向量为$x=\{x_1,x_2,x_3\}$，其中$x_i\in \{0,1\}$表示对第$i$个物品的决策，0表示不放入背包，1表示放入。解向量$x$的所有取值构成解空间。解空间为:
{ (0,0,0), (0,0,1), (0,1,0), (0,1,1),
(1,0,0), (1,0,1), (1,1,0), (1,1,1) }

3.2 组织解空间为树

3.1中定义的解空间可以用树形结构描述，如图1所示。

图1 0/1背包三个物品的解空间树形表示

因此，可以通过深度优先的方法来遍历解空间中的所有解向量。

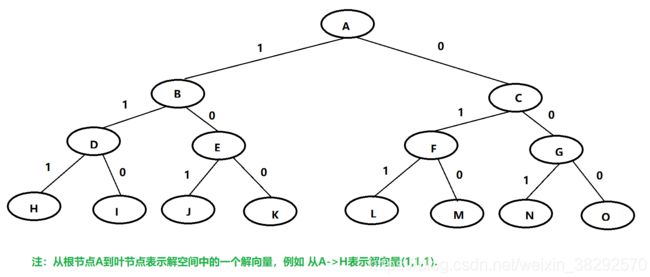
3.3 解空间组织的改进

3.2中有一个很大的问题就是，随着物品数量N的扩大，其树形解空间的叶节点数量会以指数级增长$2^N$。我们希望的是对树形的解空间搜索过程中，能够缩小搜索子树的范围，那么这将提高搜索效率。具体的剪枝策略就是：

1. 对不能放入背包的物品的节点及其子树要减掉。
2. 节点i右子树收益上界低于当前最大收益。则减掉节点i的右子树。

节点i右子树的收益上界函数定义如下：
节点i右子树的收益上界函数 = 当前节点i的收益 + 尚未考察（第i+1之后到第N个）的物品的收益；

如果遇到第一个不能装入背包的物品，就装入其一部分。我们当然希望第一个没有装入的物品其一部分会使得节点i的收益上界越大越好，因为只有这样，我们才不会漏掉可能的最优解。因此，有效的方法就是对物品按照收益密度（收益/体积）从大到小排序（见主程序main()），这样就能够使得节点i收益上界函数是最大的。代码实现如下：

/** 
* 背包界定函数 
* @param current_level, 当前二叉树层数，也是当前决策物品对象的序号，从1开始计数； 
* @return profit_bound, 返回当前节点i右子树收益值的上界， 这是当前没有搜索的节点。
*/
double profitBound(int current_level)
{
         
    double remaining_capacity = knapsack_capacity - volume_of_current_packing;    
    double profit_bound = profit_from_current_packing;
    // 按照收益密度顺序填充剩余容量    
    while (current_level <= num_of_objects && volume[current_level] <= remaining_capacity)    
    {
             
        remaining_capacity -= volume[current_level];        
        profit_bound += profit[current_level];        
        current_level ++;    
    }
    // 取第一个无法装入背包物品的一部分    
    if (current_level <= num_of_objects)    
    {
             
        profit_bound += profit[current_level] / volume[current_level] * remaining_capacity;    
    }
    return profit_bound;
}

3.4 递归回溯+剪枝实现解空间搜索最优解

这部分程序主体上和上一篇博客子集生成回溯解法相同，即访问二叉树解空间的递归形式都是：放（push或者相加）–> 递归调用下一个子节点(g(current_level + 1)) --> 不放（pop或者减去之前加上的东西） --> 递归调用下一个子节点。

但是也有不同之处，在程序上体现就是（和上一篇博客子集生成回溯解法相比），因为两处地方的剪枝而多了两个if判断。
代码实现具体如下：

/** 
* 0/1 背包递归回溯函数 
* @param curren_level, 当前二叉树层数，也是当前决策物品对象的序号, 从1开始计数； 
* @return
*/
void rKnap(int curren_level)
{
         
    // 递归出口：决策到叶子节点，即最后一个物品    
    if (curren_level > num_of_objects)    
    {
             
        max_profit_so_far = profit_from_current_packing;        
        return ;    
    }
    // 递归部分：在叶子节点之前的节点    
    if (volume_of_current_packing + volume[curren_level] <= knapsack_capacity)    
    {
             
        volume_of_current_packing += volume[curren_level];
        profit_from_current_packing += profit[curren_level];        
        rKnap(curren_level + 1);        
        volume_of_current_packing -= volume[curren_level];
        profit_from_current_packing -= profit[curren_level];    
    }
    if (profitBound(curren_level + 1) > max_profit_so_far)    
    {
             
        // 搜索右子树        
        rKnap(curren_level + 1);       
    }
}

3.5 主程序main()

实现数据的输入、对输入数据按照收益密度降序重排、输出结果。

bool cmp(pair<double, double> i, pair<double, double> j)
{
         
    return (i.first / i.second > j.first / j.second );
}
int main()
{
         
    // -1- 输入部分    
    // 物品数量和背包容积    
    cin >> num_of_objects >> knapsack_capacity;    // 物品的体积和价值    
    for(int i = 1; i <= num_of_objects; i ++) cin >> volume[i] >> profit[i];
    // -2- 回溯加剪枝    
    // 按照密度收益递减顺序排列  profit[i] 和 volumn[i]    
    vector<pair<double, double>> things;    
    for (int i = 1; i <= num_of_objects; i ++)    
    {
             
        things.push_back(make_pair(profit[i], volume[i]));    
    }    
    sort(things.begin(), things.end(), cmp);
    for (int i = 0, j = 1; i < num_of_objects; i ++, j ++)  // 注意，数组volumn和profit是从1开始计数；    
    {
             
        volume[j] = things[i].second;        
        profit[j] = things[i].first;    
    }
    // 计算最大收益    
    rKnap(1);    
    cout << max_profit_so_far << endl;
    return 0;
}

4. 程序运行过程说明

下面介绍0/1回溯剪枝的解决过程，以样例为例（物品信息见图2左上角，背包容量为5）。样例中的回溯+剪枝过程如图2所示（以深搜的顺序遍历节点），其中绿色的叉表示，再放入下一个物品就超出背包容量， 即剪枝策略1。红色的叉表示，表示的是剪枝策略2（剪枝策略见3.3）。

图2 四物品的回溯+剪枝求解过程

以节点J到节点U的过程再次解释剪枝策略2：

• 节点J处，curren_level = 4，profit_from_current_packing = 6，max_profit_so_far = 6
• 所以节点J的 profitBound(curren_level + 1) = profitBound(5) = profit_from_current_packing = 6
• 因为节点J的 profitBound(curren_level + 1) = 6并没有大于max_profit_so_far，所以，U被剪枝。

剪枝后的回溯法中， 可行解到最优解的过程是：
A - B - D - I - S, max_profit_so_far = 6；
A - B - E - K - V, max_profit_so_far = 7；
A - C - F - L - Y, max_profit_so_far = 8；
将放入背包中的物品视为一个子集，模仿上一篇回朔法子集生成中的程序修改rKnap(int curren_level)，也可以验证图2的分析结果是正确的。修改后代码运行结果如下：

图3 回溯剪枝过程中被放入背包的物品（样例特殊，可以通过物品体积区分）

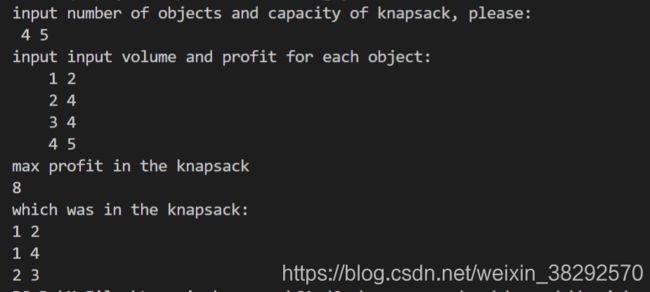
由图3可知，第一轮被放入背包物品的体积是1和2，在样例中这正好对应是第一和第二个物品，也就是对应树形解空间中的A - B - D - I - S, max_profit_so_far = 6；其余的以此类推。

5. 算法复杂度分析

以图2为例，可以知道算法最糟糕的情况是最优解出现在树形的最右面的一个分支[0，0，…，0]，也就是说没有任何物品能够放入背包（物品体积太大），这种情况下，需要遍历树形解空间所有叶节点。所以，回溯剪枝算法时间复杂度是$O(2^N)$, 其中N是物品的数量。

参考文献

[1] https://www.acwing.com/problem/content/2/
[2] 萨特吉$\cdot$ 萨尼《数据结构、算法与应用》第2版.机械工业出版社.