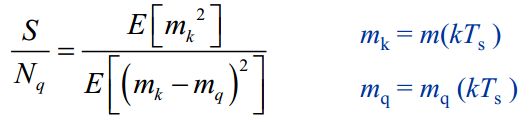模拟信号数字化02-----采样信号的量化

        前面已经了解了采样定理，经过采样，模拟信号数字化完成了第一步-----时间的离散，采样信号的量化完成模拟信号数字化第二步-----幅度的量化。

                         采样信号的量化

         模拟信号在事件上的离散化，不致引入失真，因为采样后的信号仍然是个连续变量，此连续量所包含的信息量是无限大的。若在时间上的样值进一步量化，即在取值上量化，则量化后的量化电平是离散的，包含的信息量是有限的，所以量化必然会产生量化误差，引入失真。

                                  

1.限失真编码

       编成二进制代码不可能是无失真编码，只能是在限定失真条件下的编码，称为限失真编码。

       在限定失真条件下，所需的比特数目最少的编码，是最佳限失真编码。

       主要方法是量化，包含：一维标量量化和多维矢量量化。

2.量化

       利用预先规定的有限个电平来表示模拟信号采样值得过程称之为量化。

       模拟信号经过采样得到的有无穷多个值，用N个不同的二进制数字码组来代表抽样值，N位二进制码组只能代表个不同的抽样值,必须将抽样值的范围划分成有限的M个区间,每个区间用一个电平表示， 称为量化电平。

                                 

从数学角度看，量化是将一个取值连续的无限数的集合映射到有限数集合上，是一个多对一的函数。

                         

量化过程可如图所示：

       其中，表示模拟信号，采样速率,各个采样值用蓝色点表示，第个采样值用表示，将采样值得动态范围划分成M个区间，第个区间的中点电平，即分层电平用表示，分层电平之间的间隔为量化间隔，落在量化间隔之间的样值用一个规定好的电平表示，称之为量化电平，所以量化就是将采样值转化成的过程。按图中一般量化公式进行，即，红色菱块表示量化电平值，最终量化输出为阶梯波形,实际中量化器经常是和编码过程结合在一起完成的，不一定存在独立的量化器。量化值与采样值之间的误差称之为量化误差，对于语音图像等随机信号而言，量化误差也是随机的，它像噪声一样影响通信质量，故又称为量化噪声，由图可看出量化信号是对原始信号的近似，当采样速率一定，增加量化电平数目，及量化级数目和选择适当量化电平，可以使与的近似程度提高，即量化噪声减少。
 

      

     按照限失真定理，概率密度均匀分布时，各量化区间间隔是相等的，称之为均匀量化；

                                  概率密度非均匀分布时，各量化区间间隔是不相等，称之为非均匀量化。

3.均匀量化

        1）概述

        均匀量化是把输入信号的取值域按相等间隔来分割，在均匀量化中，假设模拟信号的取值范围在中，量化电平数为M，那么量化间隔就是,那么第i个分层电平就可以表示为：,量化电平为每个量化区间的中点即：。

         那么均匀量化器的输入m与输出之间的关系可以用阶梯图表示为：

                                             

                                                

         显然量化输出电平和原抽样值及未量化的红色虚线之间是有差别的，这个差值常称为量化误差或量化噪声。显然在量化区内,即内，,在过载区内。我们可以发现，过载区的量化误差是线性增长的，而且过载误差比量化误差大，对重建信号有严重的影响。设计量化器时，要避免信号幅度进入过载区。

                                                 

                                        

      2）量化器的性能指标之一信号量噪比

       信号量噪比定义为：信号功率与量化噪声功率之比：即

                                          

假设输入模拟信号是均值为0，概率密度为的平稳随机过程，其取值范围在之间，且不出现过载量化，则量化噪声功率       信号的平均功率为：

其中，是输入样值信号的概率密度。

     3）均匀量化的缺点

      由于均匀量化的量化级数与量化间隔都是确定的，所以每个量化区间的量化噪声功率也是固定的，但是信号有大有小，同样大的噪声对大信号而言，信号量噪比也大；当信号小时，信号量噪比也小。原因是与信号样值大小无关，仅与量化间隔有关，这相当于限制了输入信号的动态范围。为解决这一问题，采用非均匀量化，在实际中也多采用非均匀量化。

4.非均匀量化（增大信噪比）

      1）实现方式

       均匀量化对于语音信号而言，有一个不足是：信号量噪比会随语音信号的减小而下降。小信号处的信号量噪比难以达到给定的要求，而语音信号的分布却是在小信号处比较集中，因此均匀量化时输入信号的动态范围将受到较大的限制。实际中多采用非均匀量化。

       非均匀量化是在输入信号的动态范围内量化间隔不相等的量化方式。即在信号样值大的地方，量化间隔大；在信号样值小的地方，量化间隔小。使得量化器输出的量化噪声在小信号区间减少，从而改善了小信号区间的信号量噪比。

                                  

        可以看出，非均匀量化是一种线性变换。实际中，非均匀量化的实现方法通常是模拟压阔法。即在进行量化前，先对信号抽样值压缩，再进行均匀量化，接收端进行扩张还原，扩张特性与压缩特性相反。

                 

      所以，压缩器就是一个非线性变换电路，能将微弱的信号放大，而将强的信号缩小。经压缩器后，小样值被放大，大样值被压小；

由此特性知接收端的扩张器与发送端压缩特性截然相反。压缩特性可由图示：

                                                

那么什么样的曲线特性符合压缩要求？

     2）压缩特性分析

      当量化区间划分很多时，在每一个量化区间内，压缩特性曲线可以看成近似直线，因此这段直线的斜率可以表示为:,假设压缩器的输入和输出都是在 ，设此压缩器的电压范围都在之间（做归一化），且纵坐标在间平均划分成个区间，则每个量化区间的间隔,带入上式得：。

      为了对不同的信号强度保持信号量噪比恒定，当输入电压减小时，应当使量化间隔按比例的减小，即正比由于，即,是一个比例常数，解方程为,将带入，得到。由于当时,与不符，所以在实用中要做适当修正。

     3)压缩律（律）

      前面推导的理想压缩特性由于不能通过原点，所以无法物理实现，故要对其进行修改。

      律：在用在处的切线代替

           

 

     参数对压缩曲线的影响：A是决定压缩程度的量，A =  1时无压缩效果，实用中选A = 87.6？律不易用电子线路准确实现，于是实际中采用13折现进行近视。

                          

      如下是A律13折现示意图，这是第一象限的8段，由于语音信号是双极性的，故还有与第一象限部分奇对称的第三部分的7段，加起来共13段。

                     

      使用13折线逼近时， x的八个段落量化分界点近似于按2的幂次递减分割，有利于数字化。使压缩特性曲线在原点附近的斜率凑成16，即，将其带入压缩特性公式：