数据结构学习笔记03-----递归的应用与联合体

例1：全排列及输出

想让子函数修改主函数中变量的值，将主函数中变量的地址做子函数的函数参数传入。如下面的交换值的函数（将主函数中两个变量的值做交换）：

void Test::swap(int * p, int * q)
{
	int t;
	t = *p;
	*p = *q;
	*q = t;
}

1.问题分析

       从n个不同元素中任取m（m≤n）个元素，按照一定的顺序排列起来，叫做从n个不同元素中取出m个元素的一个排列。当m＝n时所有的排列情况叫全排列。那么我们需要考虑两个问题：

①：如何输出（包括何时输出）

②：如何使用递归

先来看如何递归：

假设有5个元素，我们使用递归就是要把变成，假设元素是1 2 3 4 5，如何把变成： 

         我们先把第一个数和第二数交换，变成 2 1 3 4 5，对1,3,4,5进行全排列，也就是进行的操作，然后再变回

然后第一个和第三个交换，变成，对1,2,4,5进行全排列，也就是进行的操作后再变回：；

依次交换直到 ，最后换成 。

          也就是说，都是1和后面的交换，在每次换之前都是正序（递归调用时传入时的顺序，也可以看成原始顺序），这样就完成了从到的过程。

然后如何输出

       处理完全部的元素就可以输出了。也就是调用完时。

2.程序分析

int Test::permutation(int a[], int len, int start)
{
	int t = 0;
	if (len == start)
	{
		for (int i = 0; i

①：参数a[]是存放数据的数组，len是数组的长度，start可以看成处理完的数的个数，或者是目前待处理元素的起点。也就是是len == start

②：由于start是目前待处理元素的起点，所以调用时最开始它的值为0，意为一个元素也没处理，当调用时，start为1表示处理了一个。

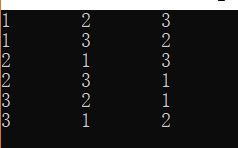
程序运行结果：

例2：组合及输出

问题分析

      ①：假设数组,假设从5个元素中取3个，那么输出也就是三个元素，由于我们仍然像全排列那样，不改变原来数组，所以我们得再使用一个新数组。当然这个数组有三个元素。

     ②：假设我们往里面放的就是，那么我们就要考虑放哪个，已经放了几个。由于是组合，我们不能输出,那么怎么解决囊？让输出一直是递增的（也就是数组提前排好序，当然输出也是递增的）。

     ③;设一个变量，表示当前要放元素的起点，由于输出一直是递增的，这样我们往中能放的元素至少是（相对于前一个放入的元素的起点，当然也可以，...）。

        还要知道放了几个，设一个变量，表示当中已经放了几个元素。

我们知道递归函数的一般结构是if(条件1)....else(条件2)....

      那么递归的终止条件，根据前面设的变量，我们很容易知道，当已放入的个数 == 数组要放的元素的个数的时候，就表示结束。终止条件程序如下：

if (filled == blen)
{
	for (int i = 0; i

那么如何递归？

else
{
    for (int i = start; i <= alen - (blen - filled); i++)
    {
        b[filled] = a[i];
        t += combination(a, alen, b, blen, filled + 1, i + 1);
    }
    return t;
}

      对于这句话，我们的数组始终没变，改变的只有数组中放的元素。假设已经b中已经放完了元素1，此时，可以放，这个过程就是循环的过程，然后再相应进行递归。

       其中参数都不变。放入元素的个数要加1（由于放入元素了，要加一）；当写完后，以后继续放入中的元素自然是

      那么放入b中的值的起点当然就是从开始，边界终点为，包含该点。此时我们可以放2,3,4，不能放5，因为要为5留出一个位置。故此时终点为3。

运行结果：

                   

 

例3：求递增子序列的最大值

        设有一个普通序列，其数值大小没有规律，子序列不是递增的，子序列是递增，又不是递增的，子序列是递增的，且长度为5,当然也是长度为5的递增子序列，没有比它再长的子序列了，故这是最长子序列，这就是我们需要求的。 

1.问题分析：

       对于序列，其输出为：，对于第一个元素2，前面没有比它小的，写1，对于第二个元素1，前面没有比它小的，也写1，对于第三个元素5，前面有两个比它小的，但是前面的两个无法构成递增，故输出为2，依次类推得到输出序列。

       同时我们也发现，输出的1,2,3,4,5实质上就是递增子序列的下标，也就是递增序列中它所排的号。

2.程序分析：

int Test::longest_increase_sub_seq(int a[], int k)
{
	int t = 1;
	if (k == 0)
	{
		return 1;
	}
	else
	{
        //下标0到k-1的都得遍历
		for (int i = k - 1; i>=0; i--)
		{
			if (a[k]>a[i])
			{
				int z = longest_increase_sub_seq(a, i) + 1;
				if (z > t)
				{
					t = z;
				}
			}

		}
		return t;
	}
}

①：函数参数k是下标，以此下标所代表的元素为终点求最长子序列，比如k = 5，就是以a[5]为终点。上面的例子是一个长度为9的数组，那么将k = 9传入函数，那么结果显然不是我们想求的该数组a的最大子序列。因为a[9]不知道是啥，如果a[9] = 1，那么最长子序列（以1为终点的最大子序列）显然就是1。

②：我们以序列为例，设6的下标为1，假设8的下标为k，那么我们只找它前面比8小的元素，比它大的不用管。

怎么做？

①：如果k = 1，return 1；

②：在[0,k-1]中找比a[k]小的元素，这个函数的返回值就是以此元素为最终元素的递增子序列的序号。那么这个序号怎么取？我们求maxValue = { }，然后将maxValue赋给t。 比如序列，显然前面序列对应的下标为，那么显然maxValue  = 2，t = maxValue  + 1 = 3。

运行结果：

for(int i = 0;i < 9;i++)
	cout << test.longest_increase_sub_seq(d, i)<<"\t";

那么如何求所有元素的最大递增子序列：

方法一：就像上面那样，通过循环调用来得到。

方法二：循环递推来实现：

void Test::longest_increase_sub_seq1(int a[], int b[], int len)
{
	int t = 1;
	for (int i = 0; ia[j])
			{
				if (b[j] + 1>t)
					t = b[j] + 1;
			}
		}
		b[i] = t;
	}
}

例4：求字符串首尾最长串

1.何为首尾最长串

       假设一字符串str，其长度为len，其首尾最长串的含义就是：存在，和，其中为a[0]到a[i]，为a[j]到a[len-1],使得。注意下标和下标不一定相同，也即的末尾元素不一定和的首元素相同。对于字符串str = ,显然我们要找的。也可以理解为和逐个相等。

2. 问题分析：

                         ①：我们不仅要找逐个元素相等的和（不止一个）。

                         ②：还要找最长的。比如,第一个元素a和最后一个元素a是一个首尾相等的串，但是最长的显然是。

                         ③：首尾相同的串有很多，但首尾最长串有很多，那么如何描述它？用一个值来描述它，此值是首串最后一个元素的下标，用这个值来描述两个串的对应关系。

                         ④：我们建立一个与等长的整数数组，用来存放对应长度的串的那个值。对于而言:

    就是以元素为结尾的串的首尾最长串的那个值，显然没有和它相等的，故写。

    就是以元素为结尾的串的首尾最长串的那个值，显然没有和它相等的，故写。  

    就是以元素为结尾的串的首尾最长串的那个值，此时第一个元素a和最后一个元素相等，首串是,其下标为0，故。

    以元素为结尾的串的首尾最长串的那个值，此时是,也是，首串的下标为1，故。

     .................

  3.程序分析

void Test::get_next(char a[], int len, int b[])
{
	b[0] = -1;
	int i, j,k = 0,t;
	for (i = 1; i < len; i++) {//访问a的所有元素
		b[i] = -1;//可能找到也可能找不到，先设置成-1
		for (j = 1; j <= i; j++) {//不断设置尾串起点
			t = 0;//首串的起点
			k = j;//尾串的起点
			while (k <= i)
			{
				if (a[t] == a[k]) {//逐个比较
					t++;
					k++;
				}
				else
					break;
			}
			if (k > i) {//说明进入while里面的if了，说明找到了
				b[i] = t - 1;
				break;
			}
		}
	}
}

①：参数是待求字符串，是数组长度，就是存值的那个数组。

②：设一个起点（尾串的起点），遍历所有元素，逐个比较首串和尾串的元素，若全相等，则找到，否则重新设置尾串起点再找

③：第一层循环是遍历,以的每一个元素做待求串的终点，第二层循环指求当前待求串的尾串的起点的设置。

运行结果：求

4.方法的改进

        由于上述方法太麻烦（三重循环），我们考虑用递推的方法。假设,其中和是字符串，x1与x2是元素，且，且是当前的首尾相等最长串。

        如果,那么我们可以知道此时的首尾最长串是；

        若,我们就要从和组成的长串中重新找比短的最长串,假设首串为，其后面的一个元素为。我们就判断和相等或不等关系。                            

                    若，则此时最长串就是；

                    若,则在中再找比A短的最长串。

关键问题：如何在和组成的长串中找和，由于 = ，所以我们只需要在中找和即可。具体如何去找我们结合程序分析。

程序分析：

的含义：首尾最长串中首串最后一个元素下标，就是我们所说的str1的最后一个元素，的含义是待处理元素下标，就是我们说的x2。

我们可以推： = ，末尾元素下标为，的值就是，表示 = 的时候的末尾元素下标。

                  那么是 当中首尾最长串的下标，即要寻找的中的最后元素下标。

 如果还没看懂，就一直心记：就是要找到的最后元素下标。（这是核心）

void Test::ger_next1(char a[], int len, int b[])
{
	b[0] = -1;
	int i, j = -1;
	for (i = 1; i < len; i++) {//对每个元素处理
		//j的含义：首尾最长串最后一个元素下标，就是我们所说的str1的最后一个元素
		//i的含义是待处理元素下标，就是我们说的x2，if语句这句话就是判断二者是否相等
		if (a[i] == a[j + 1]) {
			b[i] = j + 1;//j+1就是x1的下标
			j++;
		}
		else {
			//-1的意思就是没有首尾最长串 && x1 !=x2
			while (j != -1 && a[i] != a[j + 1]) {
                     //核心问题！核心问题！核心问题！
				j = b[j];//也就是新的A串的最后元素的下标为j，找到后继续进入循环判断，就和
			}
			if (a[i] == a[j + 1]) {
				b[i] = j + 1;
				j++;
			}
			else {
				b[i] = -1;
			}
		}
	}
}

运行结果：

 

 

                                   结构体和联合体

     1.结构体：若干个元素放在一起形成一个整体，各个元素可以共存。占用空间为所有元素占用空间的和，此时是。

struct S
{
   int no;
   int age;
};//这是结构体的声明


S  s1;//s1是结构体变量，此s1拥有no和age

     2.联合体：元素不是共存的，在下面的例子中，联合体变量u在某个时刻或者描述k，或者描述ch，占用空间为。啥时候用联合体？用在描述一个值（位置）存在两种可能性。

    【notice】：联合体中存放入一个值，用字符看是一个值，用整数看是另外一个值，即用不同的成员（字段）来看，结果不一，但是都是该值得表现。

代码1：

int main()
{
    union key{
        int k;//4个字节
        char ch[2];//两个字节
    }u;//这里定义了个变量
    u.k = 258;//现在用来描述的是k，但是此时ch中也是有值的，
    printf("%d  %d",u.ch[0],u.ch[1]);
    printf("%c%c\n", u.ch[0], u.ch[1]);//输出对应的ASCLL码
    return 0;
}

    该联合体有两个元素，分别为整数和字符数组，其中整数占四个字节（左边是低位），大于，故该联合体占四个字节。由于258 = 1*256 + 2，其内存可以看成如下：

2

1

0

0

     由此分析，可知u.ch[0] = 2,u.ch[1] = 1。以字符的形式打印的话出来的是码值（第二行）。

代码2： 

u.ch[0] = '1';//49
u.ch[1] = '2';//50
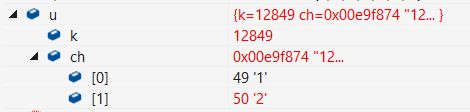
printf("%d\n ", u.k);

    若执行以下代码，及给联合体赋两个字符，即在处给字符1，查美国标准信息交换码知道字符1实际内存中存储的是49，同理字符2是50，那么u.k就是49+50*256 = 12849。 其内存各变量值为：