数据分析笔记-岭回归与Lasso回归

岭回归：

1、定义及原理

岭回归(英文名：ridge regression, Tikhonov regularization)是一种专用于共线性数据分析的有偏估计回归方法，实质上是一种改良的最小二乘估计法，通过放弃最小二乘法的无偏性，以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法，对病态数据的拟合要强于最小二乘法

在线性回归那里提到，如果我们的X矩阵存在不满秩或者几列数据相关性过强时，就会导致误差偏大。
因此为解决上述问题在原函数后加一个正则项来将不适定问题转化为适定问题。
即：$$j(\beta )=\sum (y-x\beta {)}^2+\sum \lambda {\beta }^2$$
用矩阵来表示的话就是
$$J(\beta ）=(y-X\beta {)}^{\prime }(y-X\beta )+\lambda {\beta }^{\prime }\beta$$
所以在之后的求解过程中要求解β和λ，类似线性回归可以推导为：
$$\beta =(X^{\prime }X+\lambda I{)}^{-1}{X}^{\prime }y$$
那么 λ该怎么取，这里采用了交叉验证法：
1、将数据集分成若干个变量大致相等的不重叠数据组k
2、然后从这几组中选取k-1做模型训练，1组做模型测试
3、我们可以以迭代的方式去不同的λ值，然后用于上述的验证测试，那么不同λ就会得到一个模型得分。从而选取合适的λ

2、Python实现：

from sklearn.linear_model import Ridge,RidgeCV
RidgeCV(
    alphas=(0.1, 1.0, 10.0),  #这里就是选取的不同λ，numpy array of shape
    fit_intercept=True,  #是否计算拟合截距项
    normalize=False,     #是否对数据标准化处理
    scoring=None,       #指定用于评估模型的度量方法，这里可以参考文档查有哪些方面的评估方法，比如:neg_mean_squared_error
    cv=None,             #指定交叉验证重数，k
)

# 模型拟合
ridge_cv.fit(X_train,y_train)
# 返回最佳λ值
ridge_best_Lambda = ridge_cv.alpha_
ridge_best_Lambda

#最后把ridge_best_Lambda传递给Ridge函数，拟合即可
ridge = Ridge(alpha = ridge_best_Lambda,normalize = True)
ridge.fit(X_train,y_train)

# 返回岭回归系数
pd.Series(index = [Intercept'] + X_train.columns.tolist(),data = [ridge.intercept_]+ridge.coef_.tolist()]

3、应用实例

import pandas as pd
import numpy as np
from sklearn import model_selection
from sklearn.linear_model import Ridge,RidgeCV
import matplotlib.pyplot as plt
# 读取糖尿病数据集
diabetes = pd.read_excel(r'G:\desktop\diabetes.xlsx', sep = '')
# 构造自变量（剔除患者性别、年龄和因变量）
diabetes

predictors = diabetes.columns[2:-1]
# 将数据集拆分为训练集和测试集
X_train, X_test, y_train, y_test = model_selection.train_test_split(diabetes[predictors], diabetes['Y'],test_size = 0.2, random_state = 1234 )

# 构造不同的Lambda值
Lambdas = np.logspace(-5, 2, 200)
# 构造空列表，用于存储模型的偏回归系数
ridge_cofficients = []
# 循环迭代不同的Lambda值
for Lambda in Lambdas:
    ridge = Ridge(alpha = Lambda, normalize=True)
    ridge.fit(X_train, y_train)
    ridge_cofficients.append(ridge.coef_)

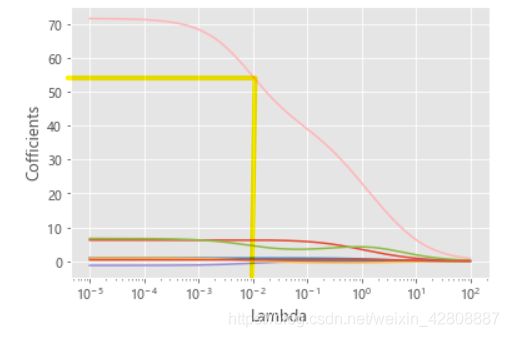
# 绘制Lambda与回归系数的关系
# 中文乱码和坐标轴负号的处理
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False
# 设置绘图风格
plt.style.use('ggplot')
plt.plot(Lambdas, ridge_cofficients)
# 对x轴作对数变换
plt.xscale('log')
# 设置折线图x轴和y轴标签
plt.xlabel('Lambda')
plt.ylabel('Cofficients')
# 图形显示
plt.show()

# 岭回归模型的交叉验证
# 设置交叉验证的参数，对于每一个Lambda值，都执行10重交叉验证
ridge_cv = RidgeCV(alphas = Lambdas, normalize=True, scoring='neg_mean_squared_error', cv = 10)
# 模型拟合
ridge_cv.fit(X_train, y_train)
# 返回最佳的lambda值
ridge_best_Lambda = ridge_cv.alpha_
ridge_best_Lambda

# 得到最佳lambda=0.013509935211980266

from sklearn.metrics import mean_squared_error
# 基于最佳的Lambda值建模
ridge = Ridge(alpha = ridge_best_Lambda, normalize=True)
ridge.fit(X_train, y_train)

# 返回岭回归系数
result = pd.Series(index = ['Intercept'] + X_train.columns.tolist(),data = [ridge.intercept_] + ridge.coef_.tolist())
print(result)
# 预测
ridge_predict = ridge.predict(X_test)
# 预测效果验证
RMSE = np.sqrt(mean_squared_error(y_test,ridge_predict))
RMSE
#输出结果：53.123616946619705

LASSO回归

1、定义与原理

LASSO是由1996年Robert Tibshirani首次提出，全称Least absolute shrinkage and selection operator。该方法是一种压缩估计。它通过构造一个惩罚函数得到一个较为精炼的模型，使得它压缩一些回归系数，即强制系数绝对值之和小于某个固定值；同时设定一些回归系数为零。因此保留了子集收缩的优点，是一种处理具有复共线性数据的有偏估计。

这里其实跟岭回归一样也是引入一个L约束

2、Python实现

类似岭回归，求得最佳Lambda然后代入岭回归函数

# LASSO回归模型的交叉验证
lasso_cv = LassoCV(alphas = Lambdas, normalize=True, cv = 10, max_iter=10000)
lasso_cv.fit(X_train, y_train)
# 输出最佳的lambda值
lasso_best_alpha = lasso_cv.alpha_
lasso_best_alpha


# 基于最佳的lambda值建模
lasso = Lasso(alpha = lasso_best_alpha, normalize=True, max_iter=10000)
lasso.fit(X_train, y_train)
# 返回LASSO回归的系数
pd.Series(index = ['Intercept'] + X_train.columns.tolist(),data = [lasso.intercept_] + lasso.coef_.tolist())

# 预测
lasso_predict = lasso.predict(X_test)
# 预测效果验证
RMSE = np.sqrt(mean_squared_error(y_test,lasso_predict))
RMSE

# 输出结果：53.06143725822573，可见这里比岭回归拟合要好一些