【推荐】2019 Java 开发者跳槽指南.pdf(吐血整理) >>> ![]()
二叉树又称为红黑树,是一种每个节点最多有两个子节点的数据结构,两个节点分别有左右之分,称为左子树和右子树,并且顺序不能颠倒。二叉树的遍历有前序,中序和后序遍历,以及广度优先遍历(也成为层序遍历)。这四种遍历方式都是相对于根节点而言的,假设有根节点A和左右子节点B、C,前序遍历顺序为ABC,中序遍历顺序为BAC,后序遍历顺序为BCA,广度优先遍历顺序则为ABC。可以看出这里的遍历次序是相对于根节点A而言的,A先于左右子节点被访问,则称为前序遍历,A在左右子节点访问的中间被访问则称为中序遍历,A后于左右子节点被访问则称为后序遍历,而广度优先遍历则是一层一层的从左往右进行遍历。对于如图A所示的二叉树,我们则有如下所示的遍历顺序:
图A
前序遍历:ABDHEICFJG
中序遍历:HDBIEAFJCG
后序遍历:HDIEBJFGCA
层序遍历:ABCDEFGHIJ
对于前序,中序和后序遍历,使用递归的方式实现较为简便,并且代码也容易阅读。我们可以定义recursive(BinaryNode
对于二叉树的每个节点,我们需要使用一个辅助的内部类来保存每个节点的信息,该内部类有三个域,分别保存左子节点,右子节点的引用以及当前数据,具体的代码如下:
private static class BinaryNode {
BinaryNode(AnyType theElement) {
this(theElement, null, null);
}
BinaryNode(AnyType theElement, BinaryNode lt, BinaryNode rt) {
element = theElement;
left = lt;
right = rt;
}
AnyType element;
BinaryNode left;
BinaryNode right;
}
通过辅助的内部类,我们可以很方便的对二叉树进行前序,中序和后序访问:
- 递归前序
public void preOrder() {
if (null == root) {
return;
}
recursive(root);
}
private void recursive(BinaryNode node) {
// 访问当前结点
visit(node);
// 访问左子节点
if (null != node.left) {
recursive(node.left);
}
// 访问右子节点
if (null != node.right) {
recursive(node.right);
}
}
- 递归中序
public void inOrder() {
if (null == root) {
return;
}
recursive(root);
}
private void recursive(BinaryNode node) {
// 访问左子节点
if (null != node.left) {
recursive(node.left);
}
// 访问当前结点
visit(node);
// 访问右子节点
if (null != node.right) {
recursive(node.right);
}
}
- 递归后序
public void laterOrder() {
if (null == root) {
return;
}
recursive(root);
}
private void recursive(BinaryNode node) {
// 访问左子节点
if (null != node.left) {
recursive(node.left);
}
// 访问右子节点
if (null != node.right) {
recursive(node.right);
}
// 访问当前结点
visit(node);
}
从上述代码中可以看出,使用递归对二叉树进行前序,中序和后序访问的时候变化的只是visit(BinaryNode
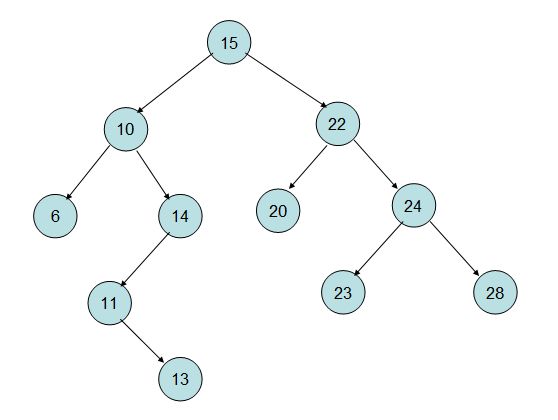
对于二叉树的非递归访问,我们则必须分别整理清楚二叉树的前序、中序、后序以及层序遍历的实际过程,首先我们看如图B所示的二叉树
图B
对于如图B所示的二叉树,根据我们前面讲述的前序遍历的规则,我们可以得出前序遍历的顺序为:
15 10 6 14 11 13 22 20 24 23 28
首先,当前结点处于根节点15的位置,ABC三角对应于15、10、22,根据前序的规则,首先访问三角根节点,即15被打印出来;接着访问左子节点,当前结点切换到10,此时10、6、14也组成一个三角,首先访问三角根节点,10被打印出来;然后访问6,当前结点被切换到6,6和它的左右子节点组成一个三角,根据前序规则,首先打印6,其次访问左子节点,由于左子节点为空,转而访问右子节点,由于右子节点也为空,当前三角访问完成,此时返回到10、6、14的三角,该三角的左子节点访问完成,进而访问该三角的右子节点14,当前结点切换到14。14和其左右子节点组成一个三角,首先访问14,14被打印出来;依次类推,直至访问完成。
从上边的分析可以看出,对于二叉树的先序遍历,我们访问了一个节点之后继而访问其左子节点,再访问左子节点的左子节点,访问完之后还要依此顺序的倒序返回回来进而访问右子节点,这里很明显需要用到栈来帮我们实现“先访问后退出”的遍历顺序。从前面的分析我们也总结出前序遍历的顺序为,首先访问当前结点,然后当前结点入栈,当前结点切换到左子节点,继续访问当前结点并且入栈,当前结点切换到左子节点,直至当前结点为空,此时当前结点所在三角访问完毕,从栈中弹出一个元素,由于该元素已经访问过,因而将当前结点切换到该节点的右子节点并访问当前结点,继续将当前结点入栈,访问当前结点的左子节点,以此类推。这里面有三个关键点:
- 当前结点沿链的左子节点一直访问;
- 当当前结点为空时从栈中弹出元素将当前结点切换到该元素的右子节点;
- 重复1和2的步骤
具体的实现代码如下:
public void preOrder() {
if (null == root) {
return;
}
Stack> stack = new Stack<>();
BinaryNode pointer = root;
while (true) {
if (null != pointer) {
visit(pointer);
stack.push(pointer);
pointer = pointer.left;
} else {
if (stack.isEmpty()) {
break;
}
pointer = stack.pop().right;
}
}
} 对于图B所示的二叉树,如果我们使用中序遍历的方式,遍历次序如下:
6 10 11 13 14 15 20 22 23 24 28
中序遍历按照“左子树-->当前结点-->右子树”的顺序进行遍历,对于二叉树而言,由于二叉树排布有一个规则,即对于每个节点,其左子树的所有节点都小于当前结点的值,其右子树的值都大于当前结点的值。因而按照中序遍历的方式,最终得到的结果将是有序的,从上述遍历次序我们也可以看出这一点。
对于中序遍历,首先当前结点处于15处,而三角ABC分别对应15、10、22。根据中序的遍历规则(B-->A-->C),首先访问的是左子树,因而当前结点切换到10处,此时遍历三角变为10、6、14,因为对于当前结点而言,其左子节点不为空,因而必须先访问当前结点的左子节点(即6),当前结点切换到6。此时当前结点和其左右子节点(虽都为空节点)组成三角,虽然6的左右子节点都为空,但是还是得将当前结点切换到6的左子节点,因为对于一个空子树而言,其已经相当于被完全遍历了。通过判空我们已经知道6的左子树遍历完全,根据中序遍历规则,此时我们可以对6进行访问了,然后将当前结点切换到6的右子节点,由于当前结点为空,右子树被访问完全,因而当前三角访问完毕,当前结点切换到10处,并且10所在左子树被完全访问完毕,因而可以访问10所在节点,访问完毕后当前结点切换到其右子树,即14,由于14的左子树没有被访问,因而当前结点切换到14的左子节点11,根据前面对6所在节点的分析,因为11所在节点为空,因而当前结点切换到其左子树(空子树)之后即访问完全了,当前结点切换回11,并对11进行访问,接着访问其右子树。依此类推,从而对整棵树进行遍历。
从上边的访问我们可以看出,中序遍历从根节点开始,沿着向左的链依次向左进行判空,直至左子节点为空即可访问该节点,然后访问其右子节点,访问完右子节点之后沿着该链返回,继续访问上一左子节点。很明显,这里是先进后出的访问次序,因而在访问过程中需要借助栈来协助我们进行中序遍历。
中序遍历有三条规则:
- 从当前结点(初始为根节点)依次切换到其左子节点,沿途元素入栈;
- 当当前结点为空时表示当前子树访问完毕,从栈顶弹出元素,当前结点指向该元素并访问该元素;
- 当前结点切换到其右子节点,重复1和2的步骤;
具体的实现代码如下:
public void inOrder() {
if (null == root) {
return;
}
Stack> stack = new Stack<>();
BinaryNode pointer = root;
while (true) {
if (null != pointer) {
stack.push(pointer);
pointer = pointer.left;
} else {
if (stack.isEmpty()) {
break;
}
pointer = stack.pop();
visit(pointer);
pointer = pointer.right;
}
}
} 比较前序和中序的非递归遍历方式,可以发现,前序和中序遍历,变化的只是访问节点的位置不同。对于后序递归,其访问方式相较于前序和中序较为复杂,我们还是以图B所示二叉树对其访问方式进行讲解,首先以后序方式访问该二叉树,其遍历次序为:
6 13 11 14 10 20 23 28 24 22 15
对于后序递归,首先当前结点处于15所在节点,15、10、22三个节点组成一个ABC三角,根据后序遍历规则(B-->C-->A),我们将当前结点切换到10所在节点;此时10与其左右子节点组成三角,根据后序遍历规则,我们先得访问10的左子树,当前结点切换到6所在节点;此时6与其左右子树(空子树)组成三角,因而当前结点要切换到6的左子节点;此时当前结点为空,因为空子树即为被完全访问的子树,因而6的左子树被访问完全,当前结点被切换到6的右子树,此时当前结点也为空,因而6的右子树被访问完全,当前结点切换回6所在节点,进而对6进行访问;此时10的左子树被访问完全,当前切点切换到10所在节点的右子节点14,此时14与其左右子树组成访问三角,当前结点切换到11;11与其左右子树组成三角,当前结点切换到11的左子节点,由于当前结点为空,因而当前结点切换回11,然后切换到其右子节点13,与6的访问类似,13被访问完全,当前结点切换回11并且对11进行访问;接着当前结点切换回14,由于其右子节点为空,因而其右子节点也顺序访问完全,此时当前结点切换回14并对其进行访问,14访问完成之后10所在结点的左右子树都被访问完全,因而10将被访问;以此类推,将整棵树访问完全。
从上述的分析可以看出,在对二叉树进行后序遍历的时候每个节点初次访问都需要通过当前结点访问到其左子节点,待左子节点访问完毕后又返回到当前结点,然后访问其右子节点,待右子节点访问完毕之后也返回到当前结点,此时才可以对当前结点进行访问。因而后序非递归遍历二叉树需要有一个域来保存结点是从左子树还是右子树返回的,如果是从右子树返回的才可以对当前结点进行访问。额外的域用枚举来保存,代码如下:
private class StackElement {
Tag tag;
BinaryNode node;
StackElement(BinaryNode n, Tag t) {
node = n;
tag = t;
}
}
enum Tag{
LEFT, RIGHT
} 对于后序遍历,从根节点开始,当前结点依次切换到其左子节点,待当前结点为空时从左子节点返回,然后访问其右子节点,这里也用到了先进后出的访问顺序,因而需要借助于栈来协助我们进行后序遍历。对于后序遍历,需要注意的点如下:
- 若当前结点(初始为根节点)不为空则将其入栈,将当前结点切换到其左子节点;
- 若当前结点为空则获取栈顶元素(此时是从左子树返回),将当前结点切换到该元素的右子树;
- 若右子树为空则弹出栈顶元素(此时是从右子树返回),访问该元素;若右子树不为空则重复1和2的步骤;
具体的实现代码如下:
public void laterOrder() {
if (null == root) {
return;
}
Stack> stack = new Stack<>();
StackElement pointer = new StackElement<>(root, null);
while (true) {
if (null != pointer.node) { // 依次将遍历至左子节点为空,并将元素入栈
stack.push(pointer);
pointer = new StackElement<>(pointer.node.left, Tag.LEFT);
} else {
if (stack.isEmpty()) {
return;
}
pointer = stack.peek(); // 左子树元素访问完毕,查看栈顶元素
if (pointer.tag == Tag.RIGHT) { // 若为右路返回则访问当前元素,并将其弹出
visit(pointer.node);
stack.pop();
pointer.node = null;
} else { // 若为左路返回则继续访问右路子节点,并将tag标记为RIGHT
pointer.tag = Tag.RIGHT;
pointer = new StackElement<>(pointer.node.right, Tag.LEFT);
}
}
}
} 至此,我们已经将前序、中序和后序的递归和非递归算法都讨论完毕了,而二叉树的层序遍历我们使用不多,这里简要讨论一下思路,并附上代码。
二叉树的层序遍历即从上往下从左往右依次遍历。首先我们从根节点开始,将根节点入队列,然后弹出队列第一个元素,访问该元素,若其左右子元素不为空,我们就将其左右子元素入队列,按照此顺序依次访问直至队列为空,从而实现对二叉树的层序遍历。具体的代码如下:
public void breadthOrder() {
Queue> queue = new LinkedList<>();
queue.add(root);
BinaryNode pointer = null;
while (!queue.isEmpty()) {
pointer = queue.remove();
visit(pointer);
if (null != pointer.left) {
queue.add(pointer.left);
}
if (null != pointer.right) {
queue.add(pointer.right);
}
}
}