【DP】日本Indeed公司机试题 - Number of Paths
Problem Statement
There is a grid of square cells with H rows and W columns. The celss at the i-th row and the j-th column (1 ![]() i
i ![]() H, 1
H, 1 ![]() j
j ![]() W) will be denoted as (i, j).
W) will be denoted as (i, j).
Each cell in this grid is painted white or black. The colors of the cells are represented by H strings ![]() ,
, ![]() , ...,
, ..., ![]() , each of length W. The cell (i, j) (1
, each of length W. The cell (i, j) (1 ![]() i
i ![]() H, 1
H, 1 ![]() j
j ![]() W) is painted white if the j-th character of the string
W) is painted white if the j-th character of the string ![]() is ' . ', and painted black if that character is ' # '.
is ' . ', and painted black if that character is ' # '.
Answer Q questions. the q-th question (1 ![]() q
q ![]() Q) is as follows:
Q) is as follows:
- A cell (
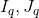 ) is specified. Find the number of ways, modulo
) is specified. Find the number of ways, modulo 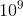 + 7, to travel from the top-left cell (1, 1) to tthe bottom-right cell (H, W) via the cell (
+ 7, to travel from the top-left cell (1, 1) to tthe bottom-right cell (H, W) via the cell (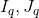 ), by repeatedly moveing right or down to the adjacent cell, visiting only white cells.
), by repeatedly moveing right or down to the adjacent cell, visiting only white cells.
Constrains
- 1
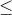 H, W
H, W 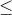 500
500 - For each i (1
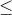 i
i 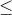 H), the length of
H), the length of 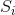 is W (每个字符串长度一定是 W )
is W (每个字符串长度一定是 W ) - For each i (1
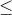 i
i 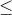 H), each character of
H), each character of 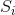 is ' . ' or ' # '. (字符串中的字符只可能是 ' . ' or ' # ' 这两种)
is ' . ' or ' # '. (字符串中的字符只可能是 ' . ' or ' # ' 这两种) - 1
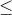 Q
Q 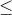 100000 (最多可能会有10万个Questions)
100000 (最多可能会有10万个Questions) - 1
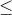
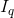
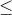 H (1
H (1 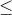 q
q 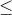 Q)
Q) - 1
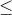
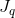
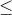 W (1
W (1 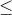 q
q 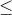 Q)
Q) - For each q (1
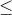 q
q 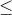 Q), the cell (
Q), the cell (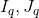 ) is white(必须经过的点一定是white,也就是能走的)
) is white(必须经过的点一定是white,也就是能走的) - The cells (1, 1) and (H, W) are white(起始点和终止点一定是white,也就是能走的)
Input
Input is given from Standard Input in the following format:
Output
Pint Q lines. The q-th line (1 ![]() q
q ![]() Q) shoule contain the answer to the q-th question.
Q) shoule contain the answer to the q-th question.
Sample Input 1 Sample Output 1
Sample Input 2 Sample Output 2
解:
遇到这种矩阵中从左上到右下的题目,第一反应就是dp,用dfs或者bfs一定会超时,核心思想就是对于不是第一行第一列的位置,dp[i][j] = dp[i - 1][j] + dp[i][j - 1],dp[i][j] 表示的就是从左上角到达这个位置的路径数,当然,如果这个位置在地图中是 '#',那么dp值就是0,左上角的dp值为1。计算dp矩阵的方式为:
- 先创建一个比原矩阵大一行一列的dp矩阵
- 然后对dp矩阵第一行第二位dp[0][1]进行赋值(或者第一列第二行),目的就是dp[1][1]的计算
- 按顺序遍历dp矩阵中剩下的位置,对其进行赋值
dp矩阵计算完成后,我们就知道从左上角起,不走 '#' 格子,达到任意可行的格子的路径数,这当然也包括最右下角的格子。
不过这道题的要求是计算必须经过一个点的情况下,从左上角到右下角的路径数。我一开始的想法就是对于每个question,复制一下dp矩阵,然后以必须经过的那个位置为左上角,计算它到右下角的这个小的dp矩阵,这样就知道从这个位置到达右下角的路径数,再乘上原dp矩阵这个位置(![]() )的值,就是结果。也就是:
)的值,就是结果。也就是:
从左上角到(![]() )的路径数 * 从 (
)的路径数 * 从 (![]() ) 到右下角的路径数 = 从左上角,经过(
) 到右下角的路径数 = 从左上角,经过(![]() ),到右下角的路径数。
),到右下角的路径数。
代码如下:
#include
#include
#include
using namespace std;
int main() {
int H = 0, W = 0;
cin >> H >> W;
string S;
vector > m(H, vector(W, ' '));
for (int i = 0; i < H; i++) {
cin >> S;
for (int j = 0; j < S.length(); j++)
m[i][j] = S[j];
}
// 计算dp矩阵, 全初始化为0,就不需要考虑 '#' 的问题了!!
vector > dp(H + 1, vector(W + 1, 0)); // 到达i,j的方式, dp矩阵
dp[0][1] = 1;
for (int i = 1; i <= H; i++) // 计算dp矩阵每一个位置的值
for (int j = 1; j <= W && m[i - 1][j - 1] == '.'; j++)
dp[i][j] = (dp[i - 1][j] + dp[i][j - 1]) % 1000000007;
int Qs = -1, iq = -1, jq = -1;
cin >> Qs;
while (Qs > 0) { // 每一个Question
--Qs;
cin >> iq >> jq; // 题目中左上角正好是(1, 1)不是(0, 0),所以正好对上
vector > tdp = dp;
// 如果必须经过的点在边界上,那么结果就是这个位置的dp值,因为没有别的路可以走(从这个位置到右下角只有一条路)
if (iq == H || jq == W)
cout << (int)(dp[iq][jq] % 1000000007) << endl;
else {
// 让必须经过的点下边的点的值都变成 1,如果是'#',本来就是0,不需要变
for (int i = iq + 1; i <= H && m[i - 1][jq - 1] == '.'; i++)
tdp[i][jq] = 1;
// 让必须经过的点右边的点的值都变成 1,如果是'#',本来就是0,不需要变
for (int j = jq + 1; j <= W && m[iq - 1][j - 1] == '.'; j++)
tdp[iq][j] = 1;
// 重新计算原dp矩阵右下角这部分每个位置的值,如果是'#',本来就是0,不需要变
for (int i = iq + 1; i <= H; i++)
for (int j = jq + 1; j <= W && m[i - 1][j - 1] == '.'; j++)
tdp[i][j] = (tdp[i - 1][j] + tdp[i][j - 1]) % 1000000007;
cout << (int)(tdp[H][W] * dp[iq][jq] % 1000000007) << endl;
}
}
} 但是上边的方式相当于对于每一个question,都重新计算了一个小的dp矩阵,这时就体现出刷题经验的重要性了,看到题目的constrain中提到了,这个地图的大小其实是不大的,大的数是question数,最多有10万个question,也就是要计算10万个小dp矩阵的值,肯定会超时。所以一定不是对于每个question单独计算dp,而是有一种方式能够记录从 (![]() ) 到右下角的路径数。
) 到右下角的路径数。
我的思维一直被困在从左上到右下这个方式中,想了很久也没想到怎么不用重新计算就知道每个位置到右下角的路径数。导致题目最终超时没有得分。机试结束了师姐想到了一个应该是正确答案的方法,就是,我先计算从左上角到地图中每个位置的路径数,也就是我上边计算出来的dp矩阵,然后!然后计算从右下角出发,只能向左或想上走,到达矩阵中每个位置的路径数!!这样我们就知道地图右下角到每个位置的路径数,也就是每个位置 (![]() ) 到右下角的路径数。。
) 到右下角的路径数。。
机试结束了所以没法提交看是否AC,不过测试用例都是过了,而且从算法时间复杂度分析应该不会超时。比较需要注意的细节就是,读入的 (iq, jq) 如果为 (3, 3) 表示矩阵左上角 (0, 0 ) 到 (2, 2) 位置的路径数,在dp矩阵中则为 (3, 3) (因为上侧,左侧各加一行一列),在rdg矩阵中则为 (2, 2) (在下侧,右侧各加一行一列)。
int main() {
int H = 0, W = 0;
cin >> H >> W;
string S;
vector > m(H, vector(W, ' '));
for (int i = 0; i < H; i++) {
cin >> S;
for (int j = 0; j < S.length(); j++)
m[i][j] = S[j];
}
// 计算从左上角到地图中任意位置的dp矩阵,全初始化为0,就不需要考虑 '#' 的问题了
vector > dp(H + 1, vector(W + 1, 0)); // 到达i,j的方式, dp矩阵
dp[0][1] = 1;
for (int i = 1; i <= H; i++)
for (int j = 1; j <= W && m[i - 1][j - 1] == '.'; j++)
dp[i][j] = (dp[i - 1][j] + dp[i][j - 1]) % 1000000007;
// 计算从右下角到地图中任意位置的rdp矩阵(reverse),也就是地图任意位置到地图右下角的路径数
vector > rdp(H + 1, vector(W + 1, 0)); // 到达i,j的方式, dp矩阵
rdp[H][W - 1] = 1;
for (int i = H - 1; i >= 0; i--)
for (int j = W - 1; j >= 0 && m[i][j] == '.'; j--)
rdp[i][j] = (rdp[i + 1][j] + rdp[i][j + 1]) % 1000000007;
int Qs = -1, iq = -1, jq = -1;
cin >> Qs;
while (Qs > 0) { // 每一个Question
--Qs;
cin >> iq >> jq; // 题目中左上角是(1, 1)不是(0, 0),所以正好对上
cout << (int)(dp[iq][jq] * rdp[iq - 1][jq - 1] % 1000000007) << endl;
}
} 计算了一下耗时,用的例子是 400 * 400 个全是 '.' 的地图,question为50000个,全是必须经过 (200, 200) 点 ,发现结果是负值,所以应该计算每个位置的时候就 % 1000000007(这应该也是测试用例最后一个wrong answer的原因),而不是只在最后计算。上述代码为修改后的。
修改后,快版的代码(第二个)用时 43.789s,可能是输出耗时比较多吧;我最开始写的代码,跑了十分钟还没有结束我就给它关了。。
最后还是要说一下没有可考虑的漏洞,就是地图大小为1*1的时候这个算法是有问题的,不过加个判断其实就行了。


