数据结构与算法|第四章：链表

数据结构与算法|第四章：链表

1.项目环境

• jdk 1.8
• github 地址：https://github.com/huajiexiewenfeng/data-structure-algorithm
  • 本章模块：chapter03

2.数组 VS 链表

数组和链表的内存分布如下

为了方便理解，这里的链表直接采用 Java 中的 LinkedList 表示。

从图中可以看到数组需要一块连续的内存空间来存储，对内存的要求较高；假设我们申请 100M 的内存空间，当内存中没有连续的满足 100M 的内存大小时，即使总体剩余空间大于 100M，也会申请失败。

而链表可以很好的解决这个问题，因为它并不需要连续的内存空间，它通过 “指针” 将一些零散的内存块串联起来，只要内存剩余满足 100M 即可。

3.单链表

链表通过 “指针” 将一组零散的内存块串联在一起，我们将内存块称为链表的 Node 节点。为了将所有的 Node 节点串联起来，每个 Node 节点除了存储数据之外，还需要一个指针来指向下一个节点的地址。我们把这个指针叫做后继指针 next。

• 头节点
  • 链表的第一个节点，通过这个节点可以遍历得到整个链表的所有元素
• 尾节点
  • 链表的最后一个节点，它的 next 节点为 null

3.1 插入节点

数组在插入和删除元素时，为了保持内存数据的连续性，需要做大量的数据搬移工作，所有时间复杂度是 O(n)；而在链表中插入或者删除一个节点，我们不需要保持内存数据的连续性，不存在数据搬移，所以在链表中插入和删除节点是一个非常快的操作，我们只需要考虑相邻节点的 “指针” (引用关系) 即可，时间复杂度为 O(1)。

比如在节点 B 和节点 C 中插入节点 D，只需要设置 B 的 next = D，设置 D 的 next = C 即可。

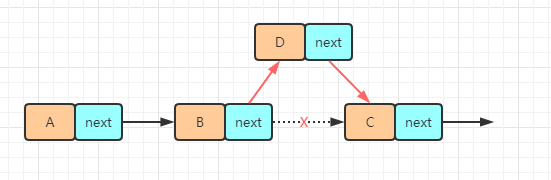
3.2 删除节点

删除节点 B，设置节点 A 的 next = 节点 C。

但是链表的缺点也非常明显，如果想要找到位置为 n 的元素，就只能从头节点依次查找 n 次，才能找到对应的元素，因为内存不联系，所以无法像数组一样通过寻址公式进行计算，链表查找的时间复杂度为 O(n)。

4.循环链表

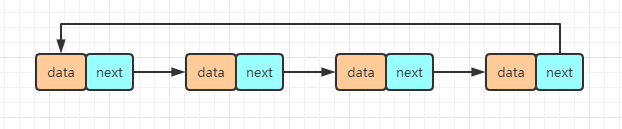
循环链表是一种特殊的单链表。它跟单链表唯一的区别就在尾结点。单链表的尾结点指针指向空地址，表示这就是最后的结点了，而循环链表的尾结点指针是指向链表的头结点。

5.双向链表

双向链表和单项链表的区别就是每个节点多了一个 prev 指针指向当前节点的上一个节点。虽然在存储上浪费了一定的空间，但是可以支持双向遍历，增加了链表的灵活性。

我们可以看看 Java 中的 LinkedList 中设计的 Node 数据结构

    private static class Node<E> {
     
        E item;
        Node<E> next;
        Node<E> prev;

        Node(Node<E> prev, E element, Node<E> next) {
     
            this.item = element;
            this.next = next;
            this.prev = prev;
        }
    }

• item 就表示上图中的 data
• 同样存在 next 和 prev 两个节点引用

双向链表对比单向链表的优势也非常明显， 如果我们已经知道 C 节点，需要删除这个节点的前驱(prev) B 节点，我们只需要获取 B 节点的上一个节点 A，设置 A 节点 next = C，设置 C 的 prev = A 即可，时间复杂度为 O(1)。而单项链表必须从头节点进行遍历，时间复杂度为 O(n)。

6.数组链表性能对比

时间复杂度比对

操作	数组	链表
插入、删除	O(n)	O(1)
随机访问	O(1)	O(n)

内存分布

数组需要确定固定大小，而且是连续的内存空间，即使 Java 中的 ArrayList 支持动态扩容，但是每次还是会申请一个固定大小的内存。动态扩容之后，将原数据拷贝到新数组中，也非常消耗性能。但是链表本身是没有大小限制的。

7.如何使用链表实现 LRU 缓存淘汰算法？

缓存是我们常用的一种优化查询的技术，但是缓存的大小有限，当缓存被用满时，哪些数据应该被清理出去，哪些数据应该被保留？这就需要缓存淘汰策略来决定。

常见的策略有三种：

• 先进先出策略 FIFO（First In，First Out）
• 最少使用策略 LFU（Least Frequently Used）
• 最近最少使用策略 LRU（Least Recently Used）

了解了题目，我们看看如何使用今天学习的链表来进行实现 LRU 算法

第一种情况，新数据 B 访问有序链表，如果发现 B 已经存在，那么删除 B 在链表中的位置，然后将 B 插入到链表的头部

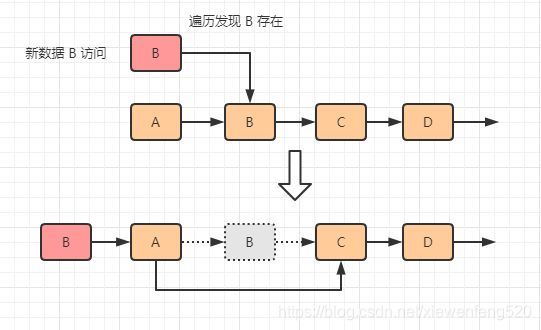
第二种情况，如果新数据 E 不存在链表中

• 如果缓存未满，将节点 E 插入到链表的头部
  
• 如果缓存已满，删除链表的尾节点，并将节点 E 插入到链表的头部
  

这样就已经使用链表实现完成了，因为不管插入的元素是什么，缓存是否已满，我们都需要遍历一次链表，所以时间复杂度为 O(n)。

8.LeetCode 题目

反转一个单链表。

示例:

输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/reverse-linked-list/

单链表结构：

public class ListNode {
     
    int val;
    ListNode next;

    ListNode(int x) {
     
        val = x;
    }
}

题解：

class ReverseLinkedListSolution {
     
    public ListNode reverseList(ListNode head) {
     
        ListNode prev = null;
        ListNode curr = head;
        while (curr != null) {
     
            ListNode next = curr.next;
            curr.next = prev;
            prev = curr;
            curr = next;
        }
        return prev;
    }
}

时间复杂度：O(n)

空间复杂度：O(1)

图解

prev：上一个节点

curr：当前节点

元素链表

循环 1 次之后

循环 2 次之后

以此类推循环 5 次之后

9.小结

上一章的数组和本章的链表都是数据结构中比较基础，常用的数据结构，和数组相比，链表更适合插入和删除，查询复杂度相对数组更高。

10.参考

• 极客时间 -《数据结构与算法之美》王争