棋盘覆盖问题(分治策略)
在棋盘覆盖问题中,可将棋盘转换为二维数组,通过改变元素值,从而实现棋盘覆盖,利用分治策略,不断将区域划分为四部分,在不同区域加入特殊点,直到覆盖整个棋盘。
一、题目重述
在一个2^k*2^k个方格组成的棋盘中,恰有一个方格与其他方格不同,称该方格为一特殊方格且称该棋盘为一特殊棋盘。利用L型骨牌对特殊棋盘进行覆盖,要求骨牌不得重叠覆盖。

图1 k=2时的一个特殊棋盘

图2 四种L型骨牌
二、解决方案
用分治策略当k>0,将2^k*2^k棋盘等分割为4个2^(k-1) * 2^(k-1)子棋盘。特殊方格必位于4个较小子棋盘之一中,其余3个子棋盘中无特殊方格,为了将无特殊方格的子棋盘转化为特殊棋盘,可以利用一个L型骨牌覆盖这3个较小棋盘的会合处,如下图所示。
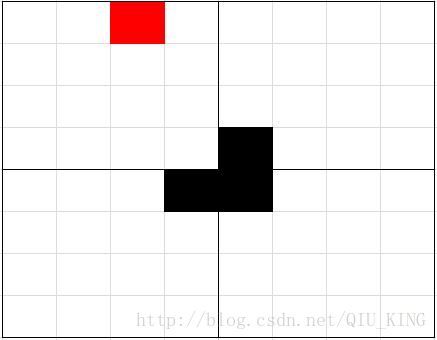
图3 棋盘分割(红色为特殊方格)
这3个子棋盘上被L型骨牌覆盖的方格就成为该棋盘上的特殊方格,从而将原问题转化为4个较小规模的棋盘覆盖问题。递归地使用这种分割,直至棋盘简化为1*1棋盘。
为了显示简单,我们将棋盘转化为二维数组,方格变换为数组元素,以0为初始化,以-1为特殊方格,以数字填充数组,同数字表示属于同一块L型骨牌,不同数字表示不同骨牌。
三、代码实现
1. 数据设置
const int number = 8;//棋盘列格数,注意要满足2^k=number,k为正整数
int C_B[number][number] = { 0 };//创建number*number的棋盘
static int temp = 1;//用于填补,作为L型骨牌
struct Point{
int line;//行坐标
int column;//列坐标
};2.特殊点设置
Point set_point()//设置特殊点
{
Point point;
int temp = 0;
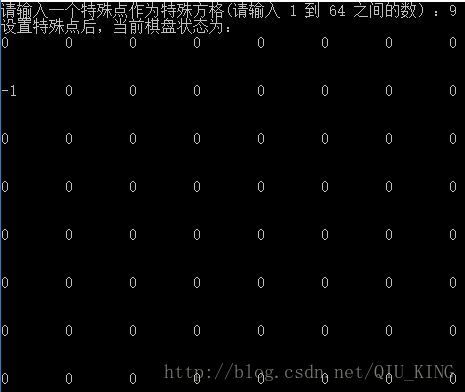
cout << "请输入一个特殊点作为特殊方格(请输入 1 到 " << number*number << " 之间的数):";
cin >> temp;
point.line = (temp - 1) / number;//特殊点所在行,注意行和列均是从0开始算起,
//之所以减一,是因为在number*k的数与number*k-1虽然在同一行,但除去 number时,却得到的是不同的值。为了改变这个临界,减一即可实现
point.column = temp - point.line*number - 1;//特殊点所在列
C_B[point.line][point.column] = -1;//值置为 -1 以表示特殊点
return point;
}3.棋盘覆盖递归函数
/*
point0为特殊点;
C_point_LU为要覆盖区域中心最小矩阵左上角点;
C_point_RU为要覆盖区域中心最小矩阵右上角点;
C_point_LD为要覆盖区域中心最小矩阵左下角点;
C_point_RD为要覆盖区域中心最小矩阵右下角点;
S_point_LU_lu为要覆盖区域左上角的四分之一区域的最左上角点;
S_point_RU_lu为要覆盖区域右上角的四分之一区域的最左上角点;
S_point_RU_rd为要覆盖区域右上角的四分之一区域的最右下角点;
S_point_LD_lu为要覆盖区域左下角的四分之一区域的最左上角点;
S_point_LD_rd为要覆盖区域左下角的四分之一区域的最右下角点;
S_point_RD_rd为要覆盖区域右下角的四分之一区域的最右下角点;
*/void Cover(Point point0, Point S_point_LU_lu, Point S_point_RD_rd)//进行棋盘覆盖
{
Point C_point_LU, C_point_RU, C_point_LD, C_point_RD, S_point_RU_lu, S_point_RU_rd, S_point_LD_lu, S_point_LD_rd;
C_point_LU.line = (S_point_LU_lu.line + S_point_RD_rd.line)/2;
C_point_LU.column = (S_point_LU_lu.column + S_point_RD_rd.column) / 2;
C_point_RU.line = C_point_LU.line;
C_point_RU.column = C_point_LU.column + 1;
C_point_LD.line = C_point_LU.line + 1;
C_point_LD.column = C_point_LU.column;
C_point_RD.line = C_point_LU.line + 1;
C_point_RD.column = C_point_LU.column + 1;
S_point_RU_lu.line = S_point_LU_lu.line;
S_point_RU_lu.column = C_point_RU.column;
S_point_RU_rd.line = C_point_RU.line;
S_point_RU_rd.column = S_point_RD_rd.column;
S_point_LD_lu.line = C_point_LD.line;
S_point_LD_lu.column = S_point_LU_lu.column;
S_point_LD_rd.line=S_point_RD_rd.line;
S_point_LD_rd.column = C_point_LD.column;
if ((S_point_LU_lu.column == S_point_RD_rd.column) && (S_point_LU_lu.line == S_point_RD_rd.line))//当point1和point2为同一点时,覆盖结束
return;
if ((point0.line <= C_point_LU.line) && (point0.column <= C_point_LU.column))//特殊点在覆盖区域中心左上角
{
C_B[C_point_RU.line][C_point_RU.column] = temp;
C_B[C_point_LD.line][C_point_LD.column] = temp;
C_B[C_point_RD.line][C_point_RD.column] = temp;
temp++;
Cover(point0, S_point_LU_lu, C_point_LU);//要覆盖区域左上角的四分之一区域进行覆盖
Cover(C_point_RU, S_point_RU_lu, S_point_RU_rd);//要覆盖区域右上角的四分之一区域进行覆盖
Cover(C_point_LD, S_point_LD_lu, S_point_LD_rd);//要覆盖区域左下角的四分之一区域进行覆盖
Cover(C_point_RD, C_point_RD, S_point_RD_rd);//要覆盖区域右上下角的四分之一区域进行覆盖
return;
}
if ((point0.line <= C_point_LU.line) && (point0.column > C_point_LU.column))//特殊点在覆盖区域中心右上角
{
C_B[C_point_LU.line][C_point_LU.column] = temp;
C_B[C_point_LD.line][C_point_LD.column] = temp;
C_B[C_point_RD.line][C_point_RD.column] = temp;
temp++;
Cover(point0, S_point_RU_lu, S_point_RU_rd);//要覆盖区域右上角的四分之一区域进行覆盖
Cover(C_point_LU, S_point_LU_lu, C_point_LU);//要覆盖区域左上角的四分之一区域进行覆盖
Cover(C_point_LD, S_point_LD_lu, S_point_LD_rd);//要覆盖区域左下角的四分之一区域进行覆盖
Cover(C_point_RD, C_point_RD, S_point_RD_rd);//要覆盖区域右上下角的四分之一区域进行覆盖
return;
}
if ((point0.line > C_point_LU.line) && (point0.column <= C_point_LU.column))//特殊点在覆盖区域中心左下角
{
C_B[C_point_LU.line][C_point_LU.column] = temp;
C_B[C_point_RU.line][C_point_RU.column] = temp;
C_B[C_point_RD.line][C_point_RD.column] = temp;
temp++;
Cover(point0, S_point_LD_lu, S_point_LD_rd);//要覆盖区域左下角的四分之一区域进行覆盖
Cover(C_point_LU, S_point_LU_lu, C_point_LU);//要覆盖区域左上角的四分之一区域进行覆盖
Cover(C_point_RU, S_point_RU_lu, S_point_RU_rd);//要覆盖区域右上角的四分之一区域进行覆盖
Cover(C_point_RD, C_point_RD, S_point_RD_rd);//要覆盖区域右上下角的四分之一区域进行覆盖
return;
}
if ((point0.line > C_point_LU.line) && (point0.column > C_point_LU.column))//特殊点在覆盖区域中心右下角
{
C_B[C_point_LU.line][C_point_LU.column] = temp;
C_B[C_point_RU.line][C_point_RU.column] = temp;
C_B[C_point_LD.line][C_point_LD.column] = temp;
temp++;
Cover(point0, C_point_RD, S_point_RD_rd);//要覆盖区域右上下角的四分之一区域进行覆盖
Cover(C_point_LU, S_point_LU_lu, C_point_LU);//要覆盖区域左上角的四分之一区域进行覆盖
Cover(C_point_RU, S_point_RU_lu, S_point_RU_rd);//要覆盖区域右上角的四分之一区域进行覆盖
Cover(C_point_LD, S_point_LD_lu, S_point_LD_rd);//要覆盖区域左下角的四分之一区域进行覆盖
return;
}
}4.棋盘输出
void display()//输出棋盘
{
cout << "当前棋盘状态为:" << endl;
for (int i = 0; i < number;i++)
{
for (int j = 0; j < number; j++)
cout << C_B[i][j] << "\t";
cout << endl << endl << endl;
}
}5.主函数调用
void main()
{
Point point0, point_lu, point_rd;
point_lu.line =point_lu.column= 0;
point_rd.line = point_rd.column = number-1;
point0=set_point();
cout << "设置特殊点后,";
display();
Cover(point0, point_lu, point_rd);//代入初始特殊点和区域定位点
cout << "进行棋盘覆盖后(注意:数字相同的表示属于同一块L型骨牌):" << endl;
display();
cout << "共使用 " << temp-1 << " 块L型骨牌! " << endl;
}五、结束语
本篇文章将棋盘覆盖问题抽象为数组元素替换问题,易于理解和解决问题。
本文不足的地方在于使用了过多变量去存储各个定位点的信息,使得程序较为冗杂,需要较多的存储空间。