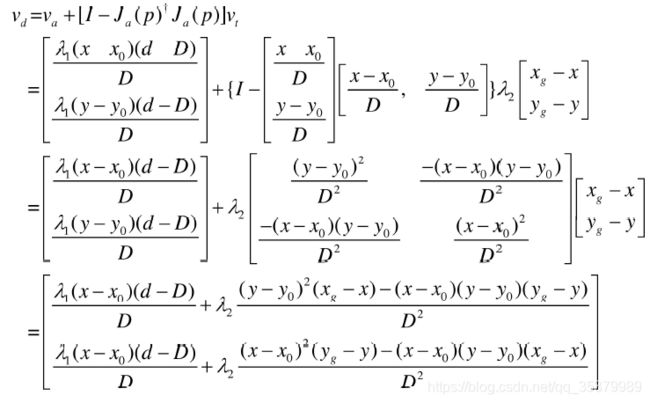基于零空间投影（NSB）行为法的多智能体控制

1 行为控制的相关概念

1.1 行为控制的定义

基于行为法的基本思想为：首先设定智能体一些期望的基本行为，每个行为都有其目标或任务。通常情况下，智能体的的行为包括避碰、 避障、 驶向目标和保持队形等。当智能体的传感器接受到外界环境刺激时， 根据传感器的输入信息作出反应， 并输出反应向量作为该行为的期望反应（方向和运动速度等）。 行为选择模块通过一定的机制来综合各行为的输出， 并将综合结果作为机器人对环境刺激的反应而输出。 设计基千行为的系统的主要问题是在设计各种基本行为以及其有效的行为协调机制。

1.2  行为控制基本方法

（1）行为抑制法：高优先级的输出抑制低优先级的输出。 这种方法虽然可以排除各任务输出之间的相互干扰， 但是必须按照优先序列来逐一完成， 任务变化时无法实时调整；

（2）加权平均法：将各个行为输出向量乘以相对应的一定的权值， 权值的大小说明了任务的相对重要性， 最后经过矢量和的形式得到一个行为输出。 该方法在任务选择上有较大改进， 但是， 对于任务实时变化时， 其动态调整的实时性不强；

（3）模糊逻辑法；根据一定的规则来综合各行为的输出， 从而确定机器人的输出， 这种方法实际上就是每个行为的权值都不是固定不变的， 而是根据任务的不同和时间的不同来实时调整的。 这样做的好处就是可以实时的调整任务权值，从而优化任务完成的质量；

（4）NSB(Null-space-based)法：由Filippo Arrichiello教授2006年提出，方法的核心是将低级任务向晕向高级任务的零空间进行投影， 将综合的任务输出作为最终的任务输出， 在完成高级任务的同时部分或全部完成低级任务。与其它基于行为方法相比， 具有实时性强、 任务之间不冲突的优点。

2 NSB方法简介

2.1 方法简介

NSB中的零空间(Null Space)是指任务执行时不使用的维度空间。 比如， 运动到某点时只需要占用X,Y的平面二维空间，此时的机器人朝向就是这个任务的零空间（这里只考虑平面上运动的情况）。

NSB方法的主要做法是首先将任务行为分解成各个简单的任务子行为， 分别列出各个子行为的任务函数， 每个子行为的任务函数都能完成对应的行为， 然后再将行为区分一定的重量级， 将低优先级的任务向量向高优先级任务的零空间投影， 得到任务综合的输出函数， 传输给底层的运动控制器控制智能体的运动。

NSB方法的核心思想是将低优先级任务的任务向量向高优先级任务的零空间上投影， 在保证高优先级任务顺利完成的同时， 部分完成低优先级任务， 并且通过投影， 避免了任务之间的相互冲突。

NSB 方法具体的数学分析如下：

假设x,y,z是惯性坐标系下的坐标， 定义智能体的位置为,对应的线速度为.对于n个智能体，定义和,为可控的任务变噩， 对应的函数关系可以表示为：

    （1）

式（1）中两边对p求导得：（其中，f(p)为关于p的函数，对p求偏导还需乘以p的导师及速度，固有如下形式）

   （2）

其中J(p)是的雅克比矩阵，不同任务根据雅克比矩阵有着不同的形式3中有举例，n是机器人的数量。求解速度得到最小二乘解：

     （3）

式（3）得到了单个任务的速度输出。如果存在多个任务， 采用NSB的方法将次要任务的速度输出投影到优先任务的零空间上。以二个任务为例， 速度输出为：

    （4）

下标表示任务的优先级。需要特别指出的是， 一个满秩的矩阵，它的零空间是零，那么低级任务在零空间上的投影也将为零， 即整个 将被过滤掉。如果存在多个任务，任务的优先序列为1,2,..., i-1, i, i+1,... 。NSB方法总是将i+1级的任务向量向i级任务投影，得到的任务向量值与i任务的和再在i-1任务的零空间上投影， 得新的到任务输出。

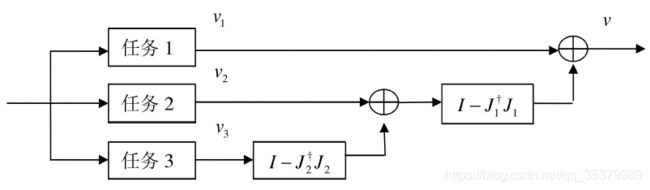
以三个子任务为例，NSB方法的协调原理可由下图清晰表示：

零空间表达式为：

2.2 需注意问题

（1）NSB方法的冲突消解机制

NSB方法在同时协调多个任务输出时，是将低级任务向高级任务的零空间上投影，从而避免低级任务与高级任务之间的冲突，也就只是部分的执行低级任务，而当低级任务与高级任务完全冲突时，低级任务将不被执行； 或者高级任务的零空间为零，即高级任务矩阵满秩，低级任务也将不被执行。
另外，可以从低级任务和高级任务的雅可比矩阵上看出两个任务之间是否有 冲突，如果两个任务的即说明两个任务向佩是正交的，那么这两个任务之间就没有冲突。 如果再加入第二个任务呢，判断方法也是一样的，即看这个任务向量与前两个任务向量是否正交，是，就说明不冲突； 否，就说明冲突。

（2）NSB方法同时执行任务的个数

NSB方法同时可以执行任务的数量是一个要着重考虑的问题，对于一个n自由度的系统，定义优先任务的维度为，任务矩阵的秩为，它的矩阵的零空间的维数就是 ; 同样定义低级任务的维度为，任务矩阵的秩为。 如果加入的低级任务不与高级任务冲突， 那么它的矩阵的零空间的维数就是 。在后续任务不冲突的情况下，任务个数可以一直叠加到I。当任务的零空间维数叠加值等于自由度的值的时候，整个零空间已经被填满，这时再加入其它任何的任务都没有效果， 因为它在零空间上的任务投影将变为零。特别注意的是： 如果低优先级任务与高优先级冲突，那么低优先级任务向量向高优先级任务的投影在零空间上将为零，意味着低优先级的任务将不被执行， 这样保证了高优先级任务的执行。

（3）NSB方法误差考量

NSB 方法在进行多智能体编队时，会产生一定的误差， 比如，通信延时会带来一定的误差，智能体的感知噪音也会带来误差， 这些误差的累积可能会导致得不到期望的编队效果。在NSB方法的实际运用时，应该根据具体的实物平台的特点和结构， 仔细分析误差的产生和来源，在合理的减小误差产生的基础上，加入合适的误差补偿佩，来使得NSB方法的机器人编队效果更佳。

3 基于NSB方法的多任务协调

3.1 二维空间内避障任务描述

假设障碍物在前进方向上，我们的目的是保持智能体与障碍物之间的安全距离。 定义,为智能体的位置；,为障碍物的位胃;,为目标点的位置。那么，智能体与障碍物之间的距离D为：

      （5）

式（5）中，就是要控制的可控变佩。定义避障的安全距离为。对可控变量求雅克比矩阵，得到：

    （6）

所以,。

根据，可以得到任务输出为：

    （7）

其中，为任务增益，需要根据任务的具体情况选取。

3.2  二维空间内运动到目标点任务描述

运动到目标点任务控制智能体向目标点行进。定义目标点的位置。智能体的位置p作为可控的任务变量,记到达位置的变量。对可控任务变量p求雅克比矩阵，得到：

   （8）

根据，同样可以得到任务输出：

为任务增益。

3.3 NSB方法综合任务输出

得到避障任务的输出和运动到目标点任务的输出后，采取NSB的方法将其综合，可以得到最终的速度输出：