Spark——基于Spark Graphx的图形数据分析

基于Spark Graphx的图形数据分析

官网指导https://spark.apache.org/docs/latest/graphx-programming-guide.html#pregel-api

一、图计算的好处

• 许多大数据以大规模图或网络的形式呈现
• 许多非图结构的大数据，常会被转换为图模型进行分析
• 图数据结构很好地表达了数据之间的关联性

二、图的概念

1、图的基本概念

• 图是由顶点集合(vertex)及顶点间的关系集合（边edge）组成的一种网状数据结构
  • 通常表示为二元组：Gragh=（V，E）
  • 可以对事物之间的关系建模
• 应用场景
  • 在地图应用中寻找最短路径
  • 社交网络关系
  • 网页间超链接关系

2、图的术语

（1）顶点（Vertex）和边(Edge)

一般关系图中，事物为顶点，关系为边

定义一个图：

Graph=(V,E)
集合V={
     v1,v2,v3}
集合E={
     (v1,v2),(v1,v3),(v2,v3)}

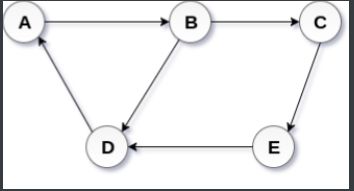
（2）有向图和无向图

• 有向图：在有向图中，一条边的两个顶点一般扮演者不同的角色，比如父子关系、页面A连接向页面B；

G=(V,E)
V={
     A,B,C,D,E}
E={
     <A,B>,<B,C>,<B,D>,<C,E>,<D,A>,<E,D>}

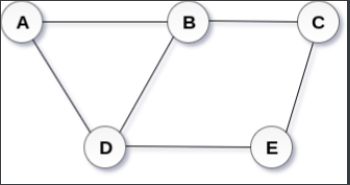
• 无向图：在一个无向图中，边没有方向，即关系都是对等的，比如qq中的好友。

G=(V,E)
V={
     A,B,C,D,E}
E={
     (A,B),(A,D),(B,C),(B,D),(C,E),(D,E)}

（3）有环图和无环图

• 有环图：有环图是包含循环的，一系列顶点连接成一个环，在有环图中，如果不关心终止条件，算法可能永远在环上执行，无法退出。

• 无环图：不包含循环，不能形成环，DAG即为有向无环图

（4）度

• 度：一个顶点所有边的数量
  • 出度：指从当前顶点指向其他顶点的边的数量
  • 入度：其他顶点指向当前顶点的边的数量

3、图的经典表示法

• 邻接矩阵：

1、对于每条边，矩阵中相应单元格值为1
2、对于每个循环，矩阵中相应单元格值为2，方便在行或列上求得顶点度数

三、Spark GraphX

1、简介

• GraphX是Spark提供分布式图计算API

• GraphX特点

  • 基于内存实现了数据的复用与快速读取
  • 通过弹性分布式属性图（Property Graph）统一了图视图与表视图
  • 与Spark Streaming、Spark SQL和Spark MLlib等无缝衔接

• 针对某些领域，如社交网络、语言建模等，graph-parallel系统可以高效地执行复杂的图形算法，比一般的data-parallel系统更快

• Graphx是将graph-parallel的data-parallel统一到一个系统中。允许用户将数据当成一个图或一个集合RDD，而简化数据移动或复杂操作。

2、GraphX核心抽象

• 弹性分布式属性图（Resilient Distributed Property Graph）
  • 顶点和边都带属性的有向多重图

• 一份物理存储，两种视图

对Graph视图的所有操作，最终都会转换成其关联的Table视图的RDD操作来完成

3、GraphX API

• Graph[VD,ED]
• VertexRDD[VD]
• EdgeRDD[ED]
• EdgeTriplet[VD,ED]
• Edge：样例类
• VertexId：Long的别名

创建一个简单的GraphX:

object MyGraghx {
     
  def main(args: Array[String]): Unit = {
     
    val conf = new SparkConf().setAppName("ghx").setMaster("local[*]")
    val sc = new SparkContext(conf)
    //建立所有的点
    val vects = sc.makeRDD(Seq((3L,("rxin","stu")),(5L,("zs","prof")),(5L,("ls","prof")),(7L,("xx","pst"))))
    //建立所有的边
    val edges = sc.makeRDD(Seq(Edge(2L,5L,"ts"),Edge(5L,3L,"zd"),Edge(5L,7L,"pi"),Edge(3L,7L,"collab")))
    //建立图
    val graph = Graph(vects,edges)
    //要添加新点
    val newPoint = sc.parallelize(Array((3L,"hehe"),(5L,"xixi"),(4L,"cici")))
    println("***********************************************************")
    graph.joinVertices(newPoint)((id,src,newval)=>(src._1+"@"+newval,src._2)).vertices.foreach(f=>println(f._2))
    println("***********************************************************")
    println(graph.numEdges,graph.numVertices,graph.edges)
    println("***********************************************************")
    graph.vertices.foreach(x=>println(x._1,x._2))
    println("***********************************************************")
    graph.edges.foreach(x=>println(x.srcId,x.dstId,x.attr))
    println("***********************************************************")
    graph.triplets.foreach(x=>println(x.srcAttr,x.dstAttr,x.attr))
    println("***********************************************************")
    graph.inDegrees.foreach(x=>println(x))
    println("***********************************************************")
    graph.degrees.foreach(println)
    println("***********************************************************")
    graph.mapEdges(e=>Edge(e.srcId,e.dstId,e.attr+",Hello")).edges.foreach(x=>println(x))
  }
}

输出结果：

***********************************************************
(zs@xixi,prof)
(xx,pst)
null
(rxin@hehe,stu)
***********************************************************
(4,4,EdgeRDDImpl[13] at RDD at EdgeRDD.scala:41)
***********************************************************
(3,(rxin,stu))
(2,null)
(7,(xx,pst))
(5,(zs,prof))
***********************************************************
(5,3,zd)
(3,7,collab)
(2,5,ts)
(5,7,pi)
***********************************************************
(null,(zs,prof),ts)
((zs,prof),(rxin,stu),zd)
((zs,prof),(xx,pst),pi)
((rxin,stu),(xx,pst),collab)
***********************************************************
(7,2)
(3,1)
(5,1)
***********************************************************
(2,1)
(3,2)
(7,2)
(5,3)
***********************************************************
Edge(2,5,Edge(2,5,ts,Hello))
Edge(3,7,Edge(3,7,collab,Hello))
Edge(5,3,Edge(5,3,zd,Hello))
Edge(5,7,Edge(5,7,pi,Hello))

4、图的算子

（1）属性算子

• 类似于RDD的map操作
  • mapVertices
  • mapEdges
  • mapTriplets

class Graph[VD, ED] {
     
  def mapVertices[VD2](map: (VertexId, VD) => VD2): Graph[VD2, ED]
  def mapEdges[ED2](map: Edge[ED] => ED2): Graph[VD, ED2]
  def mapTriplets[ED2](map: EdgeTriplet[VD, ED] => ED2): Graph[VD, ED2]
}

val t1_graph = tweeter_graph.mapVertices {
      case(vertextId, (name, age)) => (vertextId, name) }
val t2_graph = tweeter_graph.mapVertices {
      (vertextId, attr) => (vertextId, attr._1) }
val t3_graph = tweeter_graph.mapEdges(e => Edge(e.srcId, e.dstId, e.attr*7.0))

这里每一个操作产生一个新图，其顶点和边被用户定义的map函数修改了。
注意：
在每一个实例图结构不受影响。这是这些操作的关键特征，这允许结果图重复利用原始图的结构索引。下面的代码片段逻辑上是等同的，但是第一个没有保存结构索引，其不会从GraphX系统优化中获益。

（2）结构算子

• reverse
• subgraph
• mask
• groupEdges

演化一下这四个结构算子。

首先先创建一个新图，三个参数：

• users就是所有顶点的rdd（RDD[(VertexId, VD)]）
• relationships就是所有边的集合RDD[Edge[ED]]
• defaultUser是默认的顶点，也就是说如果relationships里面的源id或者目标id在users里面找不到，就会把找不到的id的那个人当成是defaultUser

val users: RDD[(VertexId, (String, String))] =
  sc.parallelize(Array((1L, ("a", "student")), (2L, ("b", "salesman")),
    (3L, ("c", "programmer")), (4L, ("d", "doctor")),
    (5L, ("e", "postman"))))

val relationships: RDD[Edge[String]] =
  sc.parallelize(Array(Edge(1L, 2L, "customer"),Edge(3L, 2L, "customer"),
    Edge(3L, 4L, "patient"), Edge(5L, 4L, "patient"),
    Edge(3L, 4L, "friend"),   Edge(5L, 99L, "father")))

val defaultUser = ("f", "none")

val graph = Graph(users, relationships, defaultUser)

然后打印一下这个图：

graph.triplets.map(
      triplet => triplet.srcAttr._1 + " ——(" + triplet.attr + ")——> " + triplet.dstAttr._1
    ).collect.foreach(println(_))

输出图中各点的关系：打印结果如下，这个graph表示的是a到f这几个人之间的关系，a是b的客户，c是b的客户，c是d的病人，c是d的病人，c是d的朋友，e是f的爸爸

a ——(customer)——> b
c ——(customer)——> b
c ——(patient)——> d
e ——(patient)——> d
c ——(friend)——> d
e ——(father)——> f

a、reverse

reverse算子的作用就是把edge的方向反过来，在这里就是把每个人的关系反过来一下
代码如下：

val reverseGraph = graph.reverse
reverseGraph.triplets.map(
  triplet => triplet.srcAttr._1 + " ——(" + triplet.attr + ")——> " + triplet.dstAttr._1
).collect.foreach(println(_))

输出结果：

-------------------------原始关系--------------------------------
a ——(customer)——> b
c ——(customer)——> b
c ——(patient)——> d
e ——(patient)——> d
c ——(friend)——> d
e ——(father)——> f
-------------------------reverse--------------------------------
b ——(customer)——> a
b ——(customer)——> c
d ——(patient)——> c
d ——(patient)——> e
d ——(friend)——> c
f ——(father)——> e

如图比较所有的关系双方都反过来了

b、subgraph

subgraph顾名思义就是取原来graph的子graph，获取子graph肯定是有条件过滤掉一部分数据，剩下来的就是子graph
代码如下：

val subGraph = graph.subgraph(vpred = (id, attr) => attr._1 > "b")
subGraph.triplets.map(
  triplet => triplet.srcAttr._1 + " ——(" + triplet.attr + ")——> " + triplet.dstAttr._1
).collect.foreach(println(_))

输出结果：

-------------------------原始关系--------------------------------
a ——(customer)——> b
c ——(customer)——> b
c ——(patient)——> d
e ——(patient)——> d
c ——(friend)——> d
e ——(father)——> f
-------------------------subgraph-------------------------------
c ——(patient)——> d
e ——(patient)——> d
c ——(friend)——> d
e ——(father)——> f

这个子graph,只保留了父graph中第一个属性比b的ascii码大的vertex

c、mask

mask算子就是求当前graph和另外一个graph的交集
代码如下，我们使用了上一个算子的结果作为当前graph进行mask的参数：

val maskGraph = graph.mask(subGraph)
    maskGraph.triplets.map(
      triplet => triplet.srcAttr._1 + " ——(" + triplet.attr + ")——> " + triplet.dstAttr._1
    ).collect.foreach(println(_))

输出结果：

-------------------------原始关系--------------------------------
a ——(customer)——> b
c ——(customer)——> b
c ——(patient)——> d
e ——(patient)——> d
c ——(friend)——> d
e ——(father)——> f
---------------------------mask-------------------------------
c ——(patient)——> d
e ——(patient)——> d
c ——(friend)——> d
e ——(father)——> f

d、groupEdges

groupEdges的作用是将2个vertex之间的所有edge进行合并，我们知道graphx处理的是多重图，多重图的特征就是2个顶点之间可能有多个平行边，这里的groupEdges就可以把这些平行边合并
代码如下：

val combineGraph = graph
  .partitionBy(PartitionStrategy.EdgePartition1D)
  .groupEdges(merge = (e1, e2) => e1 + " and " + e2)
combineGraph.triplets.map(
  triplet => triplet.srcAttr._1 + " ——(" + triplet.attr + ")——> " + triplet.dstAttr._1
).collect.foreach(println(_))

我们这里将平行边的元素用and连接起来了，这里要注意的是，使用groupEdges算子之前，必须先用一下partitionBy，不然不起作用的
打印结果如下：

-------------------------原始关系--------------------------------
a ——(customer)——> b
c ——(customer)——> b
c ——(patient)——> d
e ——(patient)——> d
c ——(friend)——> d
e ——(father)——> f
---------------------------groupEdges-------------------------------
a ——(customer)——> b
c ——(customer)——> b
c ——(patient and friend)——> d
e ——(patient)——> d
e ——(father)——> f

（3）join算子

定义一个graph来测试join：

val users: RDD[(VertexId, (String, String))] =
  sc.parallelize(Array(
    (1L, ("a", "student")), (2L, ("b", "salesman")),
    (3L, ("c", "programmer")), (4L, ("d", "doctor")),
    (5L, ("e", "postman"))
  ))

val relationships: RDD[Edge[String]] =
  sc.parallelize(Array(Edge(1L, 2L, "customer"), Edge(3L, 2L, "customer"),
    Edge(3L, 4L, "patient"), Edge(5L, 4L, "patient"),
    Edge(3L, 4L, "friend"), Edge(5L, 99L, "father")))

val defaultUser = ("f", "none")

val graph = Graph(users, relationships, defaultUser)

这个graph描述了每个人的名字和工作，这里我们给每个人增加除了名字和工作的其他属性，这个属性就是年龄属性
因此，我们需要定义一个rdd，描述每个人的年龄。
代码如下：

 val userWithAge: RDD[(VertexId, Int)] =
      sc.parallelize(Array(
        (3L, 2), (4L, 19), (5L, 23), (6L, 42), (7L, 59)
      ))

这里我们定义了id为3到7的这5个人的年龄，注意我们原来的graph的所有人的id为1到5，接下来有2种方法来把这个年龄属性加到我们graph中的每个人上面：

a、outerJoinVertices

第一种方法就是outerJoinVertices,代码如下：

graph.outerJoinVertices(userWithAge) {
      (id, attr, age) =>
      age match {
     
        case Some(a) => (attr._1, attr._2, a)
        case None => (attr._1, attr._2,"none")
      }
    }.vertices.collect.foreach(println)

b、joinVertices

第二种方法就是joinVertices,代码如下：

graph.joinVertices(userWithAge) {
      (id, attr, age) => {
     
  (attr._1 + "", attr._2 + "、" + age)
}}.vertices.collect.foreach(println)

输出结果：

-------------------------outerJoinVertices--------------------------------
(1,(a,student,none))
(2,(b,salesman,none))
(3,(c,programmer,2))
(99,(f,none,none))
(4,(d,doctor,19))
(5,(e,postman,23))
-------------------------joinVertices--------------------------------
(1,(a,student))
(2,(b,salesman))
(3,(c,programmer、2))
(99,(f,none))
(4,(d,doctor、19))
(5,(e,postman、23))

7、GraphX API 应用

• 计算用户粉丝数量

case class User(name: String, age: Int, inDeg: Int, outDeg: Int)
//修改顶点属性
val initialUserGraph: Graph[User, Int] = tweeter_graph.mapVertices{
      
     case (id, (name, age)) => User(name, age, 0, 0) 
}
//将顶点入度、出度存入顶点属性中 
val userGraph = initialUserGraph.outerJoinVertices(initialUserGraph.inDegrees) {
     
     case (id, u, inDegOpt) => User(u.name, u.age, inDegOpt.getOrElse(0), u.outDeg)
}.outerJoinVertices(initialUserGraph.outDegrees) {
     
    case (id, u, outDegOpt) => User(u.name, u.age, u.inDeg, outDegOpt.getOrElse(0))
}
//顶点的入度即为粉丝数量
for ((id, property) <- userGraph.vertices.collect) 
   println(s"User $id is ${property.name} and is liked by ${property.inDeg} people.")

8、练习

四、PageRank

1、PageRank（PR）算法

• PageRank（PR）算法670
  • 用于评估网页链接的质量和数量，以确定该网页的重要性和权威性的相对分数，范围为0到10
  • 从本质上讲，PageRank是找出图中顶点（网页链接）的重要性
  • GraphX提供了PageRank API用于计算图的PageRank

2、PageRank应用

五、Pregel

1、连通分量

• 连通分量是一个子图，其中任何两个顶点通过一条边或一系列边相互连接，其顶点是原始图顶点集的子集，其边是原始图边集的子集

class Graph[VD, ED] {
     
  def connectedComponents(): Graph[VertexID, ED]
}

2、Pregel概述

• Pregel是Google提出的用于大规模分布式图计算框架
  • 图遍历（BFS）
  • 单源最短路径（SSSP）
  • PageRank计算
• Pregel的计算由一系列迭代组成，称为supersteps
• Pregel迭代过程
  • 每个顶点从上一个superstep接收入站消息
  • 计算顶点新的属性值
  • 在下一个superstep中向相邻的顶点发送消息
  • 当没有剩余消息时，迭代结束

3、Pregel API

• initialMsg：在“superstep 0”之前发送至顶点的初始消息
• maxIterations：将要执行的最大迭代次数
• activeDirection：发送消息方向（默认是出边方向：EdgeDirection.Out）
• vprog：用户定义函数，用于顶点接收消息
• sendMsg：用户定义的函数，用于确定下一个迭代发送的消息及发往何处
• mergeMsg：用户定义的函数，在vprog前，合并到达顶点的多个消息

例子1：

object GraphPrepel extends App {
  //1、创建SparkContext
  val sparkConf = new SparkConf().setAppName("GraphxHelloWorld").setMaster("local[*]")
  val sparkContext = new SparkContext(sparkConf)

  //2、创建顶点
  val vertexArray = Array(
    (1L, ("Alice", 28)),
    (2L, ("Bob", 27)),
    (3L, ("Charlie", 65)),
    (4L, ("David", 42)),
    (5L, ("Ed", 55)),
    (6L, ("Fran", 50))
  )
  val vertexRDD: RDD[(VertexId, (String,Int))] = sparkContext.makeRDD(vertexArray)

  //3、创建边，边的属性代表 相邻两个顶点之间的距离
  val edgeArray = Array(
    Edge(2L, 1L, 7),
    Edge(2L, 4L, 2),
    Edge(3L, 2L, 4),
    Edge(3L, 6L, 3),
    Edge(4L, 1L, 1),
    Edge(2L, 5L, 2),
    Edge(5L, 3L, 8),
    Edge(5L, 6L, 3)
  )
  val edgeRDD: RDD[Edge[Int]] = sparkContext.makeRDD(edgeArray)


  //4、创建图（使用aply方式创建）
  val graph1 = Graph(vertexRDD, edgeRDD)

  /* ************************** 使用pregle算法计算 ，顶点5 到 各个顶点的最短距离 ************************** */

  //被计算的图中 起始顶点id
  val srcVertexId = 5L
  val initialGraph = graph1.mapVertices{case (vid,(name,age)) => if(vid==srcVertexId) 0.0 else Double.PositiveInfinity}

  //5、调用pregel
  val pregelGraph = initialGraph.pregel(
    Double.PositiveInfinity,
    Int.MaxValue,
    EdgeDirection.Out
  )(
    (vid: VertexId, vd: Double, distMsg: Double) => {
      val minDist = math.min(vd, distMsg)
      println(s"顶点${vid}，属性${vd}，收到消息${distMsg}，合并后的属性${minDist}")
      minDist
    },
    (edgeTriplet: EdgeTriplet[Double,PartitionID]) => {
      if (edgeTriplet.srcAttr + edgeTriplet.attr < edgeTriplet.dstAttr) {
        println(s"顶点${edgeTriplet.srcId} 给 顶点${edgeTriplet.dstId} 发送消息 ${edgeTriplet.srcAttr + edgeTriplet.attr}")
        Iterator[(VertexId, Double)]((edgeTriplet.dstId, edgeTriplet.srcAttr + edgeTriplet.attr))
      } else {
        Iterator.empty
      }
    },
    (msg1: Double, msg2: Double) => math.min(msg1, msg2)
  )

  //6、输出结果
  //  pregelGraph.triplets.collect().foreach(println)
  //  println(pregelGraph.vertices.collect.mkString("\n"))

  //7、关闭SparkContext
  sparkContext.stop()

}

//输出结果
//------------------------------------------ 各个顶点接受初始消息initialMsg ------------------------------------------
顶点3，属性Infinity，收到消息Infinity，合并后的属性Infinity
顶点2，属性Infinity，收到消息Infinity，合并后的属性Infinity
顶点4，属性Infinity，收到消息Infinity，合并后的属性Infinity
顶点6，属性Infinity，收到消息Infinity，合并后的属性Infinity
顶点1，属性Infinity，收到消息Infinity，合并后的属性Infinity
顶点5，属性0.0，收到消息Infinity，合并后的属性0.0
//------------------------------------------ 第一次迭代 ------------------------------------------
顶点5 给 顶点6 发送消息 3.0
顶点5 给 顶点3 发送消息 8.0
顶点3，属性Infinity，收到消息8.0，合并后的属性8.0
顶点6，属性Infinity，收到消息3.0，合并后的属性3.0
//------------------------------------------ 第二次迭代 ------------------------------------------
顶点3 给 顶点2 发送消息 12.0
顶点2，属性Infinity，收到消息12.0，合并后的属性12.0
//------------------------------------------ 第三次迭代 ------------------------------------------
顶点2 给 顶点4 发送消息 14.0
顶点2 给 顶点1 发送消息 19.0
顶点1，属性Infinity，收到消息19.0，合并后的属性19.0
顶点4，属性Infinity，收到消息14.0，合并后的属性14.0
//------------------------------------------ 第四次迭代 ------------------------------------------
顶点4 给 顶点1 发送消息 15.0
顶点1，属性19.0，收到消息15.0，合并后的属性15.0
//------------------------------------------ 第五次迭代不用发送消息 ------------------------------------------

例子2：

// 创建顶点集RDD
val vertices: RDD[(VertexId, (Int, Int))] = sc.parallelize(Array((1L, (7,-1)), (2L, (3,-1)),  (3L, (2,-1)), (4L, (6,-1))))
// 创建边集RDD
val relationships: RDD[Edge[Boolean]] = sc.parallelize(Array(Edge(1L, 2L, true), Edge(1L, 4L, true),  Edge(2L, 4L, true), Edge(3L, 1L, true),  Edge(3L, 4L, true)))
// 创建图
val graph = Graph(vertices, relationships)
//Pregel
val minGraph = graph.pregel(initialMsg, Int.MaxValue,  EdgeDirection.Out)(vprog, sendMsg, mergeMsg)
minGraph.vertices.collect.foreach{
     
  case (vertexId, (value, original_value)) => println(value)
}

val initialMsg = 9999
def vprog(vertexId: VertexId, value: (Int, Int), message: Int): (Int, Int) = {
     
  if (message == initialMsg)  value else (message min value._1, value._1)
}

def sendMsg(triplet: EdgeTriplet[(Int, Int), Boolean]): Iterator[(VertexId, Int)] = {
     
  val sourceVertex = triplet.srcAttr
  if (sourceVertex._1 == sourceVertex._2) Iterator.empty  else  Iterator((triplet.dstId, sourceVertex._1))
}

def mergeMsg(msg1: Int, msg2: Int): Int = msg1 min msg2

//Pregel
val minGraph = graph.pregel(initialMsg, Int.MaxValue, EdgeDirection.Out)(vprog, sendMsg, mergeMsg)
minGraph.vertices.collect.foreach{
case (vertexId, (value, original_value)) => println(value)
}

val initialMsg = 9999
def vprog(vertexId: VertexId, value: (Int, Int), message: Int): (Int, Int) = {
if (message == initialMsg) value else (message min value._1, value._1)
}

def sendMsg(triplet: EdgeTriplet[(Int, Int), Boolean]): Iterator[(VertexId, Int)] = {
val sourceVertex = triplet.srcAttr
if (sourceVertex._1 == sourceVertex._2) Iterator.empty else Iterator((triplet.dstId, sourceVertex._1))
}

def mergeMsg(msg1: Int, msg2: Int): Int = msg1 min msg2

![\[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-IZQpa4kP-1597625203080)(../../../imgs/pregel2.png)\]](https://img-blog.csdnimg.cn/20200817085122232.png#pic_center)