LeetCode第206场周赛(2020/09/13)
1. 二进制矩阵中的特殊位置
代码
class Solution {
public:
int numSpecial(vector<vector<int>>& mat) {
int N = mat.size();
int M = mat[0].size();
vector<int> sumi(N);
vector<int> sumj(M);
for(int i=0;i<N;i++)
{
for(int j=0;j<M;j++)
{
sumi[i] += mat[i][j];
sumj[j] += mat[i][j];
}
}
int ans = 0;
for(int i=0;i<N;i++)
{
for(int j=0;j<M;j++)
{
if(mat[i][j]==1)
{
if(sumi[i]==1&&sumj[j]==1)
ans++;
}
}
}
return ans;
}
};
2. 统计不开心的朋友
代码
class Solution {
public:
bool judge(int x, int y, int u ,int v, vector<vector<int>>& good, vector<bool>& unhappy)
{
if(unhappy[x])
return false;
if(good[x][u]<good[x][y]&&good[u][x]<good[u][v])
{
if(!unhappy[x])
{
unhappy[x] = true;
return true;
}
}
return false;
}
int unhappyFriends(int n, vector<vector<int>>& preferences, vector<vector<int>>& pairs) {
int ans = 0;
int N = pairs.size();
vector<vector<int>> good(n,vector<int>(n));
for(int i=0;i<n;i++)
{
for(int j=0;j<n-1;j++)
{
int person = preferences[i][j];
good[i][person] = j;
}
}
vector<bool> unhappy(n);
for(int i = 0;i<N;i++)
{
int x = pairs[i][0];
int y = pairs[i][1];
for(int j = i+1;j < N;j++)
{
int u = pairs[j][0];
int v = pairs[j][1];
if(judge(x,y,u,v,good,unhappy))
ans++;
if(judge(x,y,v,u,good,unhappy))
ans++;
if(judge(y,x,u,v,good,unhappy))
ans++;
if(judge(y,x,v,u,good,unhappy))
ans++;
if(judge(u,v,x,y,good,unhappy))
ans++;
if(judge(u,v,y,x,good,unhappy))
ans++;
if(judge(v,u,x,y,good,unhappy))
ans++;
if(judge(v,u,y,x,good,unhappy))
ans++;
}
}
return ans;
}
};
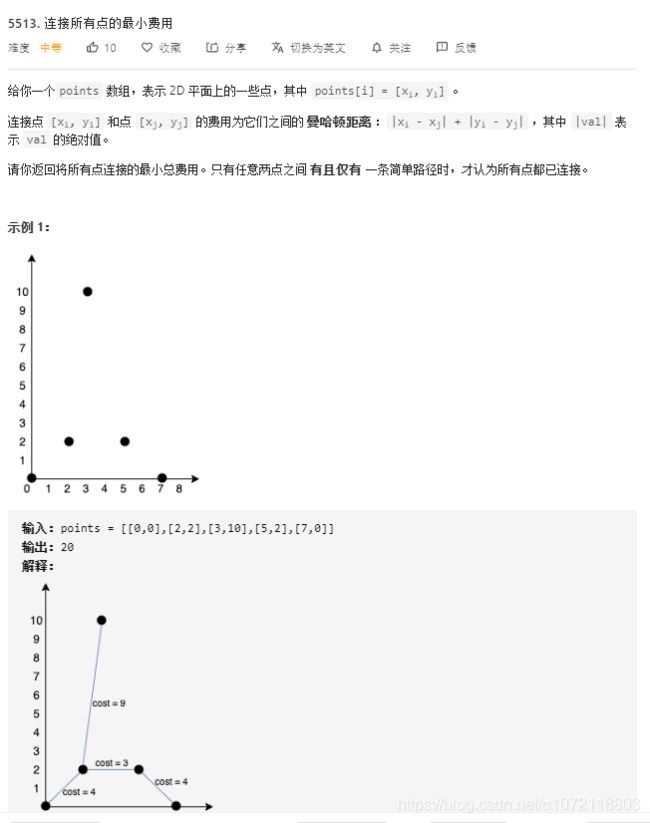
3. 连接所有点的最小费用
思路
就是个最小生成树问题,先求到各个点的哈密顿距离,然后用prim算法计算最小生成树即可。
代码
#define INF 0x3f3f3f3f
class Solution {
public:
int minCostConnectPoints(vector<vector<int>>& points) {
int N = points.size();
vector<vector<int>> costs(N, vector<int>(N,INF));
vector<int> mincost(N,INF);
mincost[0] = 0;
vector<bool> used(N, false);
for(int i=0;i<N;i++)
{
int ix = points[i][0];
int iy = points[i][1];
for(int j=i+1;j<N;j++)
{
int jx = points[j][0];
int jy = points[j][1];
costs[i][j] = abs(ix-jx)+abs(iy-jy);
costs[j][i] = costs[i][j];
}
}
int res = 0;
while(true)
{
int v = -1;
for(int u=0;u<N;u++)
{
if(!used[u]&&(v==-1||mincost[u]<mincost[v]))
v=u;
}
if(v==-1)
break;
used[v] = true;
res += mincost[v];
for(int u=0;u<N;u++)
{
mincost[u] = min(mincost[u],costs[v][u]);
}
}
return res;
}
};
4. 检查字符串是否可以通过排序子字符串得到另一个字符串
代码
class Solution {
public:
bool isTransformable(string s, string t) {
stack<int> pos[10];
int n = s.length();
for(int i=0;i<n;i++)
pos[s[i]-'0'].push(i);
for(int i=n-1;i>=0;i--)
{
int c = t[i] - '0';
//如果在s中没有这个数字
if(pos[c].empty())
return false;
for(int j = c+1; j<10; j++)
{
if(!pos[j].empty()&&pos[c].top()<pos[j].top())
return false;
}
pos[c].pop();
}
return true;
}
};