Java课程实验报告实验三——对象和类
一、实验目的
1.设计类,并画出UML类图
2.实现UML中的类
3.使用类开发应用程序
二、实验内容
1.【矩形类Rectangle】遵照9.2节中Circle类的例子,设计一个名为Rectangle的类表示矩形。这个类包括:
两个名为width和height的double型数据域,它们分别表示矩形的宽和高。width和height的默认值都为1。
创建默认矩形的无参构造方法。
创建width和height为指定值的矩形的构造方法。
一个名为getArea()的方法返回这个矩形的面积。
一个名为getPerimeter()的方法返回矩形周长。
画出该类的UML图并实现这个类。编写一个测试程序,创建两个Rectangle对象:一个矩形的宽为4高为40,另一个矩形的宽为3.5高为35.9。依次显示每个矩形的宽、高、面积和周长。
2. 【风扇类Fan】设计一个名为Fan的类表示一个风扇。这个类包括:
三个名为SLOW、MEDIUM和FAST而值为1、2、3的常量表示风扇的速度。
一个名为speed的int类型私有数据域表示风扇的速度(默认值为SLOW)。
一个名为on的boolean类型私有数据域表示风扇是否打开(默认值为false)。
一个名为radius的double类型私有数据域表示风扇的半径(默认值为5)。
一个名为color的String类型数据域表示风扇的颜色(默认值为blue)。
这四个数据域的访问器和修改器。
一个创建默认风扇的无参构造方法。
一个名为toString()的方法返回描述风扇的字符串。如果风扇是打开的,那么该方法在一个组合的字符串中返回风扇的速度、颜色和半径。如果风扇没有打开,该方法返回一个由“fan is off”和风扇颜色、半径组成的字符串。
画出该类的UML图。实现这个类。编写一个测试程序,创建两个Fan对象。将第一个对象设置为最大速度、半径为10、颜色为yellow、状态为打开。将第二个对象设置为中等速度、半径为5、颜色为blue、状态为关闭。通过调用它们的toString方法显示这些对象。
3.【二次方程式】为二次方程式ax2+bx+c=0设计一个名为QuadraticEquation的类。这个类包括:
代表三个系数的私有数据域a、b、c。
一个参数为a、b、c的构造方法。
a、b、c的三个get方法。
一个名为getDiscriminant()的方法返回判别式,b2-4ac。
一个名为getRoot1()和getRoot2()的方法返回等式的两个根。
这些方法只有在判别式为非负数时才有用。如果判别式为负,方法返回0。
画出该类的UML图。实现这个类。编写一个测试程序,提示用户输入a、b、c的值,然后显示判别式的结果。如果判别式为正数,显示两个根;如果判别式为0,显示一个根;否则,显示“The equation has no roots”。
4.【位置类】设计一个名为Location的类,定位二维数组中的最大值及其位置。这个类包括公共的数据域row、column和maxValue,二维数组中的最大值及其下标用double型的maxValue以及int型的row和column存储。
编写下面的方法,返回一个二维数组中最大值的位置。
public static Location locateLargetst(double[][] a)
返回值是一个Location的实例。编写一个测试程序,提示用户输入一个二维数组,然后显示这个数组中的最大元素及下标。运行实例如下:
输入二维数组的行数和列数: 3 4
输入数组:
23.5 35 2 10
4.5 3 45 3.5
35 44 5.5 9.6
最大元素及其下标是: 45 在(1,2)
三、实验要求:
要求每个学生独立完成实验任务。
四、实验报告
1. 实验结果与分析
(1) 实验一:Rectangle类实现
A. UML类图实现
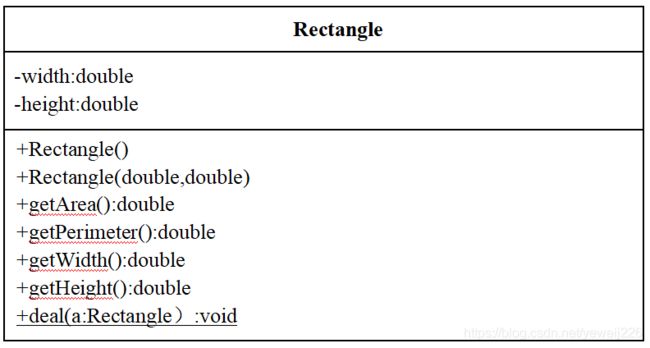
B. 运行
首先根据提示输入两个矩形的宽与高(使用题例)

回车,返回相应参数
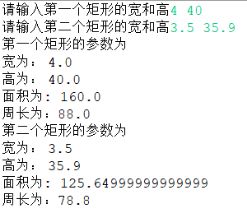
其中面积由于浮点数的不精确性而显示的是一个近似小数,可以使用格式化输出来使其两位小数输出
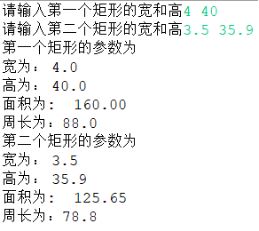
C. 结果分析
首先根据题目要求创建相关的属性和方法,其中getArea方法return的值为宽高,getPerimeter方法return的值是2(宽+高),然后在主函数中创建两个double类型量储存输入的宽和高,再用含参数的构造方法创建两个Rectangle对象并赋值,然后调用deal方法显示输出,deal方法里面为输出相关参数值,这样就实现了本题的要求。
(2)实验二:Fan类实现
A. UML类图实现

B. 运行

C. 结果分析
首先根据题目要求完成相关属性和方法的定义,其中注意三个常量SLOW,MEDIUM,HIGH的定义,四个数据域除了color为公有,其他均为私有,toString函数需要对on的值进行判断;然后在主方法中创建两个Fan类的对象并直接赋值(由于程序给定值,所以未做输入操作,意义不大),再调用两个对象的toString方法返回属性,再输出即可。
(3)实验三:QuadraticEquation类实现
A. UML类图实现
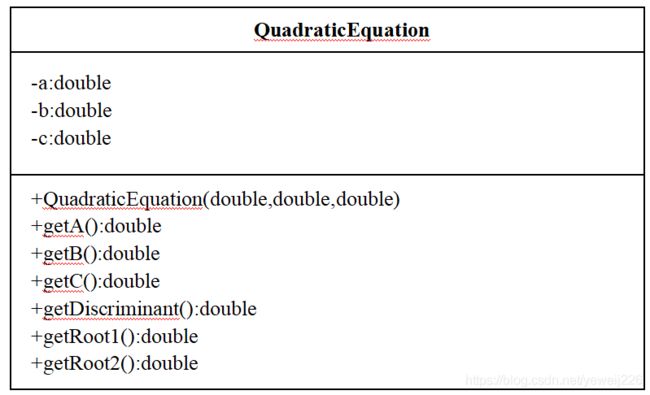
B. 运行
首先根据提示输入ax^2+bx+c的值

先输入判别式大于0的两组数
不能除尽

能除尽

再输入判别式等于0的组

再输入判别式小于0的组

C. 结果分析
首先根据题目要求完成相关属性和方法的定义,其中a,b,c均定义为私有,剩下的函数返回值均为double类型。输入a,b,c的值,然后调用getDiscriminant函数返回判别式的值,其中getDiscriminant函数内计算b^2-4ac的值,再根据返回的判别式的值来判定大于0,等于0或小于0,如果是大于0,有两个不同的根,调用getRoot1函数和getRoot2函数来返回两个根值,其中两根计算方法如题中所示;如果是等于0,有两个相同的根,调用getRoot1函数来返回这个根植(getRoot1和getRoot2值相等);如果是小于0,无解,返回“The equation has no roots”文本。
(4)实验四:Location类实现
A. UML类图实现

B. 运行
首先根据提示输入横行数和纵列数的值

然后输入行列的元素值(以本题数据为例)

回车,返回最大值及其所在位置

C. 结果分析
首先根据题目要求完成相关属性和方法的定义,其中row,column定义为公有,locateLargest函数定义为公有静态方法,传入输入的二维数组,在这个函数中,首先将(0,0)位置的值定义为初始最大值并存入max,将位置信息分别存入r,c中,设置两层循环对二维数组中的所有元素进行比较,如果比较元素大于max中的值则替换max中的值,并将新的位置存入r,c中,直到循环遍历结束,再将带有这个属性的对象返回。在主函数中首先输入row,column的值,然后设置二层循环输入元素值,然后将其赋到locateLargest函数中,返回最大值并输出。
2. 心得体会
本次的实验为类与对象的实验,类中方法给的十分明确,我们需要构建的是对这些方法的运用,在这块由于我的练习不足,速度明显比前面单纯的基础语法问题慢了一些,并在一些语法问题,如main函数的位置,二维数组的创建的问题寻求了书籍或者同学的帮助,在实现过程中因为思路还算清晰,方法的构建倒是很快就想了出来,归根究底应该是对类与对象这方面的运用还是不是很熟悉,还是要练习。
3. 源代码
Rectangle类
package experiment03;
import java.util.Scanner;
public class Rectangle{
//数据域
private double width = 1;
private double height = 1;
//无参构造方法
Rectangle(){
}
Rectangle(double newWidth,double newHeight){
width = newWidth;
height = newHeight;
}
double getArea(){
return width * height;
}
double getPerimeter(){
return 2 * (width + height);
}
double getWidth(){
return width;
}
double getHeight(){
return height;
}
public static void deal(Rectangle a){
double s1 = a.getWidth();
double s2 = a.getHeight();
double s3 = a.getArea();
double s4 = a.getPerimeter();
System.out.println("宽为: " + s1);
System.out.println("高为: " + s2);
System.out.printf("面积为: % .2f" ,s3);
System.out.println();
System.out.println("周长为:" + s4);
}
public static void main(String[] args){
Scanner input = new Scanner(System.in);
double wid,hei;
System.out.print("请输入第一个矩形的宽和高");
wid = input.nextDouble();
hei = input.nextDouble();
Rectangle rec1 = new Rectangle(wid,hei);
System.out.print("请输入第二个矩形的宽和高");
wid = input.nextDouble();
hei = input.nextDouble();
Rectangle rec2 = new Rectangle(wid,hei);
System.out.println("第一个矩形的参数为");
deal(rec1);
System.out.println("第二个矩形的参数为");
deal(rec2);
}
}
Fan类
package experiment03;
public class Fan {
final static int SLOW = 1;
final static int MEDIUM = 2;
final static int HIGH = 3;
private int speed = SLOW;
private boolean on = false;
private double radius = 5;
public String color = "blue";
public void setSpeed(int newSpeed){
speed = newSpeed;
}
public void setOn(boolean newOn){
on = newOn;
}
public void setRadius(double newRadius){
radius = newRadius ;
}
public void setColor(String newColor){
color = newColor;
}
public int getSpeed(){
return speed;
}
public boolean getOn(){
return on;
}
public double getRadius(){
return radius;
}
public String getColor(){
return color ;
}
Fan(){
}
public String toString(){
if(on){
String result = (String)("这个风扇的速度为: " + speed + ",颜色为: " + color + ",半径为: " + radius);
return result;
}
else{
String result = (String)("fan is off" + ",这个风扇的颜色为: "+ color + ",半径为: " + radius);
return result;
}
}
public static void main(String[] args){
Fan f1 = new Fan();
f1.speed = HIGH;
f1.on = true;
f1.radius = 10;
f1.color = "yellow";
Fan f2 = new Fan();
f2.speed = MEDIUM;
f2.on = false;
f2.radius = 5;
f2.color = "blue";
String f1re = f1.toString();
String f2re = f2.toString();
System.out.println("第一个风扇");
System.out.println(f1re);
System.out.println("第二个风扇");
System.out.println(f2re);
}
}
QuadraticEquation类
package experiment03;
import java.util.Scanner;
public class QuadraticEquation {
private double a;
private double b;
private double c;
QuadraticEquation(double a,double b,double c) {
this.a = a;
this.b = b;
this.c = c;
}
public double getA(){
return a;
}
public double getB(){
return b;
}
public double getC(){
return c;
}
public double getDiscriminant(){
return b * b - 4 * a * c;
}
public double getRoot1(){
if(this.getDiscriminant() < 0)return 0;
else return ((-1) * b + Math.sqrt(getDiscriminant()))/ 2 * a ;
}
public double getRoot2(){
if(this.getDiscriminant() < 0)return 0;
else return ((-1) * b - Math.sqrt(getDiscriminant())) / 2 * a ;
}
public static void main(String[] args) {
System.out.println("请输入a,b,c的值");
Scanner input = new Scanner(System.in);
double a = input.nextDouble();
double b = input.nextDouble();
double c = input.nextDouble();
QuadraticEquation re = new QuadraticEquation(a, b, c);
System.out.println(re.a + "x^2+" + re.b + "x+" + re.c + "的判别式值为" + re.getDiscriminant());
if(re.getDiscriminant() > 0){
System.out.println("该二次方程组的根为: r1 = " + re.getRoot1() + ",r2 = " + re.getRoot2());
}
else if(re.getDiscriminant() == 0){
if(re.getRoot1() != 0)
System.out.println("该二次方程组的根为: r = " + re.getRoot1());
else System.out.println("该二次方程组的根为: r = " + re.getRoot2());
}
else System.out.println("The equation has no roots");
}
}
Location类
package experiment03;
import java.util.Scanner;
public class Location {
public int row;
public int column;
public double maxValue;
public static Location locateLargest(double[][] a){
double max = a[0][0];
int r = 0;
int c = 0;
for(int i = 0;i < a.length;i++){
for(int j = 0;j < a[i].length;j++){
if(a[i][j] > max){
max = a[i][j];
r = i;
c = j;
}
else continue;
}
}
Location te = new Location();
te.row = r;
te.column = c;
te.maxValue = max;
return te;
}
public static void main(String[] args){
int row,column;
Scanner input = new Scanner(System.in);
System.out.print("Enter the number of rows and columns in the array: ");
row = input.nextInt();
column = input.nextInt();
double[][] ar = new double[row][column];
System.out.println("Enter the array: ");
for(int i = 0;i < row;i++){
for(int j = 0; j < column;j++){
ar[i][j] = input.nextDouble();
}
}
Location re = new Location();
re = locateLargest(ar);
System.out.println("The location of the largest element is " + re.maxValue + " at (" + re.row + "," + re.column + ")" );
}
}