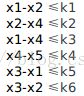差分约束系统

差分约束系统定义（引自维基百科）：如果一个系统由n个变量和m个约束条件组成，其中每个约束条件形如xj-xi<=bk(i,j∈[1,n],k∈[1,m]),则称其为差分约束系统(system of difference constraints)。亦即，差分约束系统是求解关于一组变量的特殊不等式组的方法。

例如，有如下不等式组：

我们可以把它写成如下矩阵的形式：

定义左边的矩阵为A，中间的列向量为 x, 右边的列向量为k。

我们观察一下A可以发现它和我们在离散数学中讲图的时候讲了一个关联矩阵很像。

矩阵A的特点是每行只有一个1和一个-1，其余列都是0。

而关联矩阵的特点是每列只有一个1和一个-1，其余行为0.

即A的转置矩阵就是一个关联矩阵。

那么我们想想，是否可以通过求解图的最短路径来求得不等式组的一个可行解呢？

结论是可以的。

对于每一个差分约束系统，我们根据矩阵A来建立图G（V， E），而G的关联矩阵就是A的转置矩阵，边权存在二维数组W中。假设我们现在要求单源最短路，将各个定点的最短距离存到对应的dis[v]中。最后我们要得到的结果一定满足： dis[v] <= dis[u] + w[u][v]. 变形一下得到： dis[v] - dis[u] <= w[u][v].   另dis[v] 为 Xv， dis[u]为Xu，有Xv - Xu <= w[u][v]. 可以看到当前单源最短路问题与差分约束系统问题的等价性。

故可以通过求解单源最短路来求解差分约束问题。当图中存在负环的时候，不等式组无解，否则有解，并且xi的解为dis[i]。若dis[i] = INF，则xi的值为任意值。

hdu1531是一道入门题。

题意：给定未知数的个数n，同时给出m个约束条件， 均以（Asi + Asi+1  + ... + Asi+n） < k 或者 （Asi + Asi+1  + ... + Asi+n） > k形式出现。问是否存在可行解。

定义一下sigma(n) = A1 + A2 + A3 + ... + An.

则 Ai + ... + Aj = sigma(j) - sigma(i-1).这样就可以求解了。

代码：

#include
#include
#include

using namespace std;

const int N = 128;
const int INF = 0x3f3f3f3f;

int n, m, cnt;

struct Edge {
    int v, w;
    int next;
};

int fir[N];
Edge edge[N];
int vis[N], dis[N];
int outque[N];

void init() {
    cnt = 1;
    memset(fir, -1, sizeof(fir));
}

void addEdge(int u, int v, int w) {
    edge[cnt].v = v;
    edge[cnt].w = w;
    edge[cnt].next = fir[u];
    fir[u] = cnt++;
}

bool SPFA(int s) {
    queue que;
    memset(vis, 0, sizeof(vis));
    memset(dis, INF, sizeof(dis));
    memset(outque, 0, sizeof(outque));
    dis[s] = 0;
    que.push(s);
    while(!que.empty()) {
        int cur = que.front();
        que.pop();
        outque[cur]++;
        if(outque[cur] > n) return false;
        vis[cur] = 0;
        for(int i = fir[cur]; i != -1; i = edge[i].next) {
            int v = edge[i].v;
            if(dis[v] > dis[cur] + edge[i].w) {
                dis[v] = dis[cur] + edge[i].w;
                if(!vis[v]) {
                    vis[v] = 1;
                    que.push(v);
                }
            }
        }
    }
    return true;
}

int main() {

    while(~scanf("%d", &n), n) {
        init();
        scanf("%d", &m);
        for(int i = 0; i < m; i++) {
            int s, ni, k;
            char o[6];
            scanf("%d%d%s%d", &s, &ni, o, &k);
            if(o[0] == 'g')
                addEdge(s + ni, s - 1, -k-1);
            else addEdge(s - 1, s + ni, k - 1);
        }

        for(int i = 1; i <= n; i++) {
            addEdge(n+1, i, 0);
        }

        if(SPFA(n+1))
            printf("lamentable kingdom\n");
        else printf("successful conspiracy\n");
    }
    return 0;
}