JavaScript堆排序

构建堆

本文都是最大堆。利用数组存储堆中的元素，且堆中第一个元素序号为1，子元素小于父元素

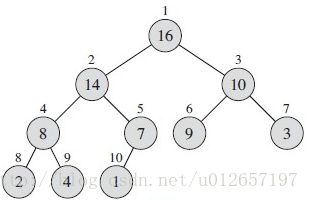
如上图：对于第i个节点，他的子节点为2i,2i+1，父节点为i/2，以数组存储堆。

1.直接插入

每当在数组末尾即最后一个叶子节点后面插入新元素，都可能破坏最大堆的性质，因此要调整堆，即比较新插入的元素和其父元素的大小，若大于父元素就和父元素交换位置，循环这个过程。

function Heap() {
    this.data = [];
    this.addPos = 1;//表示下一个可以插入的位值为addPos}
}

  Heap.prototype = {
    addItem(item){//添加元素
        this.data[this.addPos++] = item;
        this.shiftUp();//向上调整堆
    },
    shiftUp: function () {
        let k = this.addPos - 1;
        //this.addPos - 1表示最后一个元素，其大于父元素就和父元素交换，循环这个过程
        while (k > 1 && this.data[Math.floor(k / 2)] < this.data[k]) {
            this.swap(Math.floor(k / 2), k);
            k = Math.floor(k / 2);
        }
    },
     getMax(){//取堆顶元素即最大值并返回。
        let max = this.data[1];
        this.data[1] = this.data[--this.addPos];//将堆中最后一个元素赋值给堆顶元素。
        this.shiftDown(1);//从堆中第1个元素开始调整堆
        return max;

    },
    shiftDown(k){
        while (2 * k < this.addPos) {//如果第k个元素有子节点
            let j = 2 * k;//j表示孩子节点中的最大值的索引，先取左孩子节点
            if (j + 1 < this.addPos && this.data[j + 1] > this.data[j]) {//若存在右孩子节点并且右孩子结点大于左孩子节点
                j += 1;
            }
            if (this.data[j] > this.data[k]) {//若第k个元素小于孩子节点，就将其和最大的孩子节点交换位置
                this.swap(k, j);
            } else {
                break;
            }
            k = j;
        }

    },

    getSize(){
        return this.data.length;
    },
    showPrint(){
        for (let i = 0; i < this.data.length; i++) {
            console.log(this.data[i]);
        }
    },
    swap(a, b){
        let temp = this.data[a];
        this.data[a] = this.data[b];
        this.data[b] = temp;
    },
};

每次取一个元素插入到堆中，即对每个元素进行shiftUp操作，则生成堆的时间复杂度为O(nlogn);
测试：

let heap = new Heap();
let arr = [1,4,0,3,5,8];
for(let i = 0;ilet item = arr[i];
    heap.addItem(item);
}
heap.showPrint();
console.log('_____________________________');
let len = heap.addPos;
for(let i = 0;i<len;i++){
    if(heap.addPos !== 1){
        let max =  heap.getMax();
        console.log(max)
    }
}

输出结果为：

8
4
5
1
3
0
_____________________________
8
5
4
3
1
0

2.从最后一个非叶子节点调整

即将传进来的arr按照原先的顺序写成2叉树，从最后一个非叶子节点开始进行shiftDown操作，即使其子元素满足最大堆的性质。

function Heap(arr) {
    this.data = [];
    this.addPos = 1;
    this.init(arr);
}
Heap.prototype = {
    init(arr){
        this.data[0] = undefined;
        this.data = this.data.concat(arr.slice(0));
        this.addPos = this.data.length;
        let firstNoLeaf = parseInt((this.addPos - 1) / 2);
        for (let i = firstNoLeaf; i > 0; i--) {
            this.shiftDown(i);
        }
    },

    swap(a, b){
        let temp = this.data[a];
        this.data[a] = this.data[b];
        this.data[b] = temp;

    },
    shiftDown(k){
        while (2 * k < this.addPos) {
            let j = 2 * k;
            if (j + 1 < this.addPos && this.data[j + 1] > this.data[j]) {
                j += 1;
            }
            if (this.data[j] > this.data[k]) {
                this.swap(k, j);
            } else {
                break;
            }
            k = j;
        }

    },
    getMax(){
        let max = this.data[1];
        this.data[1] = this.data[--this.addPos];
        this.shiftDown(1);
        return max;

    },

    showPrint(){
        for (let i = 1; i < this.addPos; i++) {
            console.log(this.data[i]);
        }
    }
};

直接将传进来的数组从最后一个非叶子节点开始，依次向前，作为根节点进行shiftDown操作，则生成堆的时间复杂度为O(nlogn);
测试：

let arr = [1, 4, 0, 3, 5, 8];
let heap = new Heap(arr);
heap.showPrint();
console.log('_____________________________');
let len = heap.addPos;
for (let i = 0; i < len; i++) {
    if (heap.addPos !== 1) {
        let max = heap.getMax();
        console.log(max)
    }
}

输出：

8
5
1
3
4
0
_____________________________
8
5
4
3
1
0

不开辟新空间的堆排序

在上面2中init方法中构建完最大堆后，取堆顶元素（最大值）和最后一个元素交换，同时将堆的长度减1，即最后一个元素的位置已经固定，以后不需要调整，然后调整堆，然后再从堆顶开始调整堆。

function init(arr){
        this.data[0] = undefined;
        this.data = this.data.concat(arr.slice(0));
        this.addPos = this.data.length;
        let firstNoLeaf = parseInt((this.addPos - 1) / 2);
        for (let i = firstNoLeaf; i > 0; i--) {
         this.shiftDown(i);//注意这里虽然shiftDown的时间复杂度为O(logn)，但是其内只进行了一次判断，并未循环，因此时间复杂度为O(n)
            //以上是将arr调整成堆
        }
        for (let i = this.addPos - 1; i > 0; i--) {
            this.swap(1, i);
            this.addPos--;
            this.shiftDown(1);//这里从第一个元素开始调整需要循环调整，因此时间复杂度为O(logn)
        }//此时this.data 中的数据已经是排好序的了
    },

先利用2中的方法将数组调整成最大堆后，依次将堆中第一个元素和最后一个元素交换，此时，最后一个元素为最大值，
且其位置已经固定，堆长度减一，接着调整堆，重复前面的工作，这样的好处是不用开辟新的空间。速度最快，时间复杂度为O(nlogn)