音频特效：Flanger 和 Chorus

Introduction 开场白

今天要讨论的是 Flanger 和 Chorus 这两个音效，它们也是基于 Delay 实现的，并且在实现和原理上，它们又有很多相似的地方。

我们还是老规矩，先分别介绍这两种音效的具体效果，分析其实现细节，并最后给出两者的异同。

Flanger 镶边音效

首先是 flanger，中文译为“镶边”，原意指的是开盘式录音机的边缘

为了产生 flanger 音效，可以用两个开盘录音机同时播放同一段磁带。如果两个录音机播放时完全一致的，那么输出的音频只是简单的加强了原音频。为了产生 flanger 特效，我们可以轻轻按压其中一个录音机，降低其播放速率从而降低其音调，此外还会导致两个音频在时间上有稍稍差异。当我们松开按压，那么原先音调和时间差异会逐渐消失，同时我们去轻轻按压另一台录音机，这样循环反复，就产生 flanger 音效。

flanger 也被称为 “飞行”音效，它听起来就像呼啸而过的火车，像腾空而起的喷气式飞机，让我们来听一听。可以明显的感觉到 flanger 音效像是有一个飞机在脑袋上盘旋。

原始音频

flanger

说到 flanger 的产生的原理，那我们就不得不提相长干涉(Constructive Interference) 和 相消干涉(Destructive Interference)

简单来说，假设有个 sine 信号，通过 delay 然后与原始音频相加，如果两个信号在相位上完全一致，那么输出音频的幅度是输入的两倍，这就是相长干涉；如果两个信号相位刚好相抵，那么输出静音信号，这就是相消干涉。

通常一个音频具有很多很多频率，经过 delay 并与原始信号相加，那么会导致有些频率相互抵消（频率响应表现为“波谷”状），有些频率相互增强（频率响应上表现为“波峰”状）。“波峰”和“波谷”在 LFO 的作用下，发生移动和变化，从而最终产生了 flanger 音效。可以结合 flanger 在开盘录音机中操作理解这个过程：循环反复轻压录音机其实就是产生周期性 delay 的过程，这个行为与 LFO 一致。

Basic Flanger

这里给出 basic flanger 的差分方程和块状图
$$y[n]=x[n]+gx[n-M[n]]$$

其中

• $g$ 为 feedback，也被称为 depth
• $M[n]$为延迟，由 LFO 控制

basic flanger 的结构也被称为 前馈梳妆滤波器，因为它的频谱响应像一个梳子一样。通过传递方程可以解释：
$$\begin{array}{rl}Y(z)& =X(z)+g{z}^{-M[n]}X(z)\\ H(z)& =\frac{Y(z)}{X(z)}=1+g{z}^{-M[n]}\end{array}$$

令 $z=e^{j\omega }$，其中$\omega \in [0,\pi ]$，得到幅度响应
$$\begin{array}{rl}H(e^{j\omega })& =1+g{e}^{-j\omega M[n]}\\ |H(e^{j\omega })|& =\sqrt{1+2g\cos (\omega M[n])+g^2}\end{array}$$

可以看到幅度响应 $|H(e^{j\omega })|$ 是 cos 周期函数，在 $\omega \in [0,\pi ]$ 下有 $M/2$ 个 “波峰"和"波谷”

"波峰"的位置在：
$${\omega }_p=2\pi p/M$$

”波谷“的位置在:
$${\omega }_n=(2n+1)\pi /M$$

“波峰"与"波峰”、"波谷"与"波谷"之间的频率间隔是 $f_s/M$

因此幅度响应看起来就像一个梳子一样，例如下面这张 $M[n]=6$ 的幅度响应：

当 $M[n]$ 由 LFO 控制着不断变化时，“波峰”和“波谷”不断发生变化，这就产生了 flanger 音效

Flanger with Feedback 反馈Flanger

根据带反馈的 flanger 的块状图，我们可以写出其差分方程为:
$$y[n]=x[n]+g_{ff}d[n]\text{where}d[n]=x[n-M]+g_{fb}d[n-M]$$
转换为只与 $y[n]$ 和 $x[n]$ 相关的差分方程：
$$\begin{array}{rl}y[n-M]& =x[n-M]+g_{ff}d[n-M]\\ d[n]& =x[n-M]+\frac{g_{fb}}{g_{ff}}(y[n-M]-x[n-M])\\ y[n]& =x[n]+g_{fb}y[n-M]+(g_{ff}-g_{fb})x[n-M]\end{array}$$

其传递方程为:
$$H(z)=\frac{Y(z)}{X(z)}=\frac{z^M+g_{ff}-g_{fb}}{z^M-g_{fb}}$$

可以看到，当 $g_{fb}=0$ 时，其传递方程与 basic flanger 一致。当 $g_{fb}<1$ 时所有极点在单位圆内，是稳定的。

接下来直接上具体实现代码

void Flanger::processBlock(AudioBuffer<float> &buffer)
{
     
    const int num_channels = buffer.getNumChannels();
    const int num_samples = buffer.getNumSamples();
    float phase = 0.0f;
    float channel0EndPhase = phase_;

    assert(static_cast<size_t>(num_channels) <= dlines_.getNumLines());

    for(int c = 0; c < num_channels; ++c)
    {
     
        phase = phase_;
        if(stereo != 0 && c != 0)
        {
     
            phase = fmodf(phase + 0.25f, 1.0f);
        }

        float* channel_data = buffer.getWritePointer(c);
        auto* dline = dlines_.getDelayLine(c);

        for(int i = 0; i < num_samples; ++i)
        {
     
            const float in = channel_data[i];

            // get delay from lfo
            float delay_second = min_delay + sweep_width*lfo_.lfo(phase, LFO::WaveformType::kWaveformSine);
            float delay_sample = delay_second * static_cast<float>(getSampleRate());

            // get interpolation delay value
            float interpolation_val = dline->getInterpolation(delay_sample);
            channel_data[i] = in + depth * interpolation_val;

            // push input to delay line
            dline->push(in + (interpolation_val * feedback));

            // update phase
            phase += lfo_freq*invert_sample_rate_;
            if(phase >= 1.0f)
            {
     
                phase -= 1.0f;
            }
        }

        // use channel 0 only keep the phase in sync between call processBlock()
        if(c == 0)
        {
     
            channel0EndPhase = phase;
        }
    }

    phase_ = channel0EndPhase;
}

里面有一个细节需要说明下，就是立体声模式

当开启 stereo 模式时，我们要制造一种伪立体声效果。所谓“伪立体声”就是左右声道有区别，但是听者无法具体分辨其方位。立体声产生的原因：声音传到左右耳的时间差、频率差、音量差。在我们的实现中，左右声道中 LFO 的 phase 有差异，导致 delay 差异，从而产生了伪立体声。

Chorus 合唱音效

接下来要介绍的是 Chorus 合唱音效。Flanger 和 chorus 都是基于 delay 的音效，在实现上几乎是一样的。

两者最大的区别在于 delay 的长度：chorus 用的 delay 更长，通常在 20-30ms 或者以上，而 flager 通常小于 10ms，远低于人类听觉对回声的分辨极限(大概是 50-70 ms)

在音乐中，当几个音高和音色相近的声音独立演奏时，就会出现合唱音效。这种音效十分常见，例如一群人在唱同一首歌，或者在同时拉小提琴，他们总是会在音高或者时间上表现出轻微的差异即使他们在齐声演奏。这些细微的变化让声音更加丰富、更加明亮，这也是为什么大型弦乐团演奏听起来非常震撼的原因之一。chorus 音效正是模拟了这些时间和音高差，让即使只有一个乐器的音源听起来像是有几个乐器一起演奏一样。

我们来听听chorus音效效果

原始音频

chorus

Basic Chorus

这里给出 basic chorus 的差分方程和块状图

$$y[n]=x[n]+gx[n-M[n]]$$

可以看到，basic chorus 和 basic flanger 的结构是一样的，它们最主要的区别在于 delay 的长度：chorus 的 delay 长度通常在 20-30ms，而 flager 通常在 10ms 一下

Basic chorus和 basic flanger 一致，它们的幅度响应就像一个梳子一样：
$$\begin{array}{rl}|H(e^{j\omega })|& =\sqrt{1+2g\cos (\omega M[n])+g^2}\end{array}$$

我们假设 chorus 的 delay = 30ms，那么在采样率 48kHz 下，$M=1440$，因此两个波峰之间的间隔为 $f_s/M=33.3Hz$，也就说每 33.3 Hz 出现一个波峰。对于我们的听觉系统而言，33.3Hz 的频率差太小了，几乎无法分辨。

下面直接上代码

void Chorus::processBlock(AudioBuffer<float> &buffer)
{
     
    const auto num_channels = buffer.getNumChannels();
    const auto num_samples = buffer.getNumSamples();

    float ph = 0.0f;

    for(size_t c = 0; c < num_channels; ++c)
    {
     
        auto* channel_data = buffer.getWritePointer(c);
        auto* dline = dlines_.getDelayLine(c);

        ph = phase_;

        for(size_t i = 0; i < num_samples; ++i)
        {
     
            const float in = channel_data[i];
            float weight = 0.0f;
            float phase_offset = 0.0f;

            for(int j  = 0; j < num_voices - 1; ++j)
            {
     
                if(stereo != 0 && num_voices > 2)
                {
     
                    weight = (float)(j) / (float)(num_voices-2);

                    if(c != 0)
                    {
     
                        weight = 1.0f - weight;
                    }

                } else
                {
     
                    weight = 1.0f;
                }

                if(weight != 0.0f)
                {
     
                    // get delay from lfo
                    float delay_second = min_delay + sweep_width*lfo_.lfo(fmodf(ph+phase_offset,1.0f), LFO::WaveformType::kWaveformSine);
                    float delay_sample = delay_second * static_cast<float>(getSampleRate());

                    // get interpolation value
                    float interpolation_val = dline->getInterpolation(delay_sample);
                    channel_data[i] = in + weight * depth * interpolation_val;
                }

                if(num_voices < 3)
                {
     
                    phase_offset += 0.25f;
                } else
                {
     
                    phase_offset += 1.0f / (float)(num_voices - 1);
                }
            }

            dline->push(in);

            // update phase
            ph += lfo_freq*invert_sample_rate_;
            if(ph >= 1.0f)
            {
     
                ph -= 1.0f;
            }
        }
    }

    phase_ = ph;
}

其中比较复杂的是伪立体声那部分，这部分实现中，包括了频率差和音量差，其中phase_offset控制频率差，weight控制音量差。

总结

chorus 和 flanger 在结构上基本相同。主要区别在于参数的选择上：chorus 使用的延迟时长比 flanger 更长，而且通常具有更大的扫频宽度。这些参数共同导致了，原声与延迟副本之间更大的分离感和更多的音高调制。

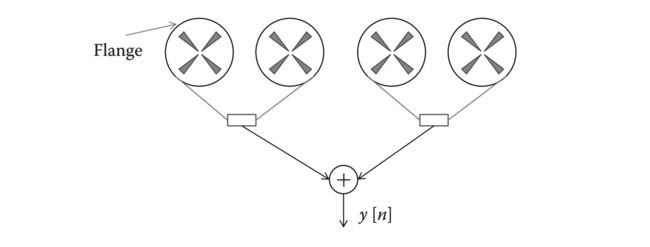
另一个结构上区别是，flanger 可以利用反馈产生更为强烈的效果，而这一点在 chorus 中几乎没有。另一方面，chorus 会使用一个以上的延迟副本，而 flanger 通常只使用一个副本。

音频特效专栏

• 音频特效：Delay 和 Vibrato
• 音频特效：Flanger 和 Chorus