PAT乙级 1007 素数对猜想(20分)

PAT乙级 1007 素数对猜想(20分)

让我们定义d​n为：d_n=p_​n+1−p_n，其中p​_i是第i个素数。显然有d₁=1，且对于n>1有d_n是偶数。“素数对猜想”认为“存在无穷多对相邻且差为2的素数”。
现给定任意正整数N(<10​⁵ )，请计算不超过N的满足猜想的素数对的个数。

输入格式:

输入在一行给出正整数N。

输出格式:

在一行中输出不超过N的满足猜想的素数对的个数。

输入样例:

20

输出样例:

4

思路：

枚举出10⁵以内的所有素数，对整个素数表依次进行判断，找出符合条件的素数对。
素数是一个非常深奥的话题，判断素数和验证素数的方法有普通素数筛法，埃氏筛法，欧拉筛法。
根据下面的统计数据可以看出，不同的筛选素数的方法在程序运行时间上有明显的区别。

统计数据：

题解 方法一：

#include 
using namespace std;

bool isprime(int a) {
     
    for (int i = 2; i * i <= a; i++)
        if (a % i == 0) return false;
    return true;
}

int main() {
     
    int N, cnt = 0;
    scanf("%d",&N);
    for (int i = 5; i <= N; i++)
        if (isprime(i-2) && isprime(i)) cnt++;
    printf("%d",cnt);
    return 0;
}

这个方法直接从0到根号N之间判断这个数是不是素数，可以说是最好理解的一种方法了。这段代码没有借助额外的空间，因此，我们仔细观察可以发现一个问题，所有待验证的数都验证了两边，对时间不友好。(当n=10是，验证了8和10. 当年12时，验证了10和12，可见10被验证了两次)。
这个方法耗时基本在15毫秒左右。

题解 方法二：

#include 
#include 
using namespace std;

const int MAXN = 110000;
int n,cnt;
vector<int> primes;

void getprimes(){
     
    int is_ok;
    for(int i=2;i<MAXN;++i){
     
        is_ok = 1;
        for(int j=0;j<primes.size() && primes[j]*primes[j]<=i;++j){
     
            if(i%primes[j]==0) {
     is_ok=0;break;}
        }
        if(is_ok) primes.push_back(i);
    }
}

int main(){
     
    getprimes();
    scanf("%d",&n);
    for(int i=0;primes[i+1]<=n;++i){
     
        if(primes[i+1]-primes[i] == 2) cnt++;
    }
    printf("%d",cnt);
    return 0;
}

优化过的朴素筛法
可以轻松跑进15毫秒

题解 方法三：

#include 
#include 
#include 
using namespace std;

const int MAXN = 110000;
vector<int> prm;
int n,cnt,tmp=1;

void get_primes(){
     
    bool *val = new bool[MAXN];
    memset(val,true,MAXN * sizeof(bool));
    for(int i=2;i<MAXN;++i){
     
        if(val[i]){
     
            prm.push_back(i);
            for(int j=i;j<MAXN/i;++j)
                val[j*i]=false;
        }
    }
}

int main(){
     
    scanf("%d",&n);
    get_primes();
    for(int i=1;prm[i]<=n;++i)
        if(prm[i] - prm[i-1] == 2) cnt++;
    printf("%d",cnt);
    return 0;
}

埃氏筛法O(NlogN) 也有说 O(NloglogN)
耗时5毫秒以内

题解 方法四：

#include 
#include 
#include 
using namespace std;

const int MAXN = 110000;
vector<int> prm;
int n,cnt,tmp=1;

void get_primes(){
     
    bool *val = new bool[MAXN];
    memset(val,true,MAXN*sizeof(bool));
    for(int i=2;i<MAXN;++i){
     
        if(val[i])
            prm.push_back(i);
        for(int j=0;j<prm.size() && i*prm[j]<MAXN;++j){
     
            val[i*prm[j]] = 0;
            if(i%prm[j]==0) break;
        }
    }
}

int main(){
     
    scanf("%d",&n);
    get_primes();
    for(int i=1;prm[i]<=n;++i)
        if(prm[i] - prm[i-1] == 2) cnt++;
    printf("%d",cnt);
    return 0;
}

欧拉筛法 O(N) 但是因为常数项比较高的原因，在小量数据范围内和埃氏筛法耗时不相上下。
耗时5毫秒以内

知识补充 程序运行时间

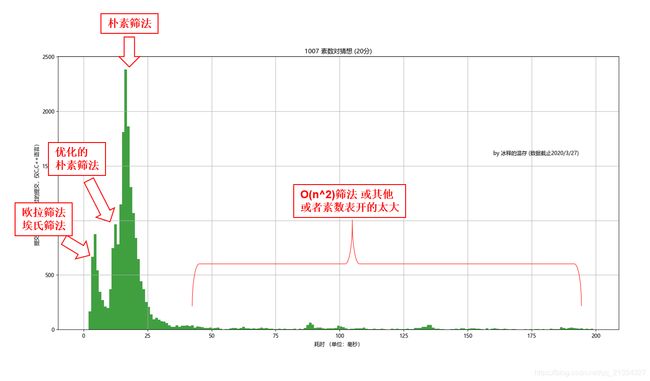
通过这道题可以看出，不同算法运行时间是有明显差距的，每当我们提交完一份代码的时候，不仅要关心代码有没有通过所有测试点，在通过所有测试点的条件下，看看自己的代码运行时间是不是也是优秀的，如果自己的代码运行速度明显比别人慢，那就要多看看博客，多看看别人的代码，自己想想还有没有优化的空间，选择一种最快的算法完成这道题。