从DFA角度理解KMP算法

KMP 算法

KMP（Knuth-Morris-Pratt）算法在字符串查找中是很高效的一种算法，假设文本字符串长度为n，模式字符串长度为m，则时间复杂度为O(m+n)，最坏情况下能提供线性时间运行时间保证。

《算法导论》和其他地方在讲解KMP算法的时候，过于数学化且晦涩难懂，我也因此迷惑了很长时间。后来看《算法（第四版）》部分的讲解，对其中最复杂的Next数组有了重新的认识。我这里也希望用通俗的语言来将我的理解分享出来。

KMP算法的本质是构造一个DFA（确定性有限状态自动机），然后通过自动机对输入的字符串进行处理，每接收一个字符，就能转移到一个新的状态，如果自动机能够达到特定的状态，那么就能够匹配字符串，否则就匹配失败。

先来了解一下DFA。
自动机分为两种：DFA和NFA（非确定性有限状态自动机），都可以用来匹配字符串。很多正则表达式引擎使用的就是NFA。

如果有过FPGA开发经验，就会很清楚，自动机与硬件描述语言中常见的状态机类似。状态机是一种流程控制的模型。一个自动机包含多个状态，状态之间可以有条件的进行转移。这个条件就是输入。

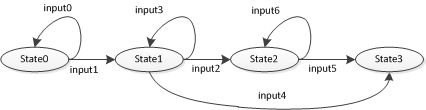
根据输入的不同，一个状态可以转移到另一个状态，或者保持当前状态。自动机可以使用下面的状态转移图来表示。

上图中State0为初始状态，如果输入为input0，就继续保持State0状态，直到输入input1，状态才转移到State1，其他状态类似。

下面我再来讲KMP算法。

朴素的字符串查找算法使用的是暴力搜索，过程大概是这样的：
假设要处理的文本字符串为s，要在其中查找字符串p（也称为模式字符串）。
先将s与p的首字符对齐，然后一个字符一个字符的对比，如果到某个字符不一样，就将p字符串右移一位，然后s与p的字符指针回退到新的对齐的位置，重新开始对比。
借用《算法（第四版）》中的代码如下，这里的i和j分别用来跟踪文本与模式字符串，i表示已经匹配过的字符序列的末端：

public static int search(String pat,String txt){
    int j,M = pat.length();
    int i,N = txt.length();
    for (i = 0, j = 0; i < N && j < M; i++){
        if (txt.charAt(i) == pat.charAt(j)){
            j++;
        }
        else{
            i -= j;//go back
            j = 0;
        }
    }
    if (j == M){
        return i - M;//match
    }
    else {
        return N;//not match
    }
}

朴素查找算法在查找的时候，其实文本字符串的某些字符在前面就已经能获取相关的信息了，但是因为算法的局限，为了不漏掉中间能够匹配的字符，下一次回退的时候，又重新匹配了一次或多次，这样浪费了一定的时间。

相比朴素的查找算法，KMP的优势在于，基本流程是一致的，不需要进行不必要的回退操作。它是用一个dfa数组（有地方叫做Next数组）来指示匹配失败的时候下一步j应该放到哪，也就是对齐的位置，这个位置不一定是朴素查找算法中的右移的一位，可能是多位，效率更高。

所以代码变成了下面的：

public static int search(String pat,String txt){
    int j,M = pat.length();
    int i,N = txt.length();
    for (i = 0, j = 0; i < N && j < M; i++){
        if (txt.charAt(i) == pat.charAt(j)){
            j++;
        }
        else{
            j = dfa[txt.charAt(i)][j];//use an array dfa[][]
        }
    }
    if (j == M){
        return i - M;//match
    }
    else {
        return N;//not match
    }
}

代码和前面的朴素查找基本一样。

关键是这个dfa[][]数组怎么计算，这也是弄懂KMP的关键所在。

其实这个dfa[][]数组，就是DFA自动机的一个简单的模型。txt.charAt(i)就是输入，j作为状态。

举个例子：模式为ABABAC
该例子构造的DFA的状态转移图如下：

可以看到，最初在状态0，然后每次输入新的字符，都会转移到新的状态或者保持旧状态。
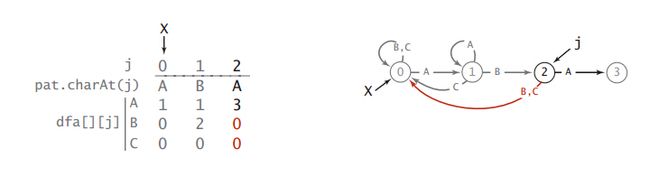
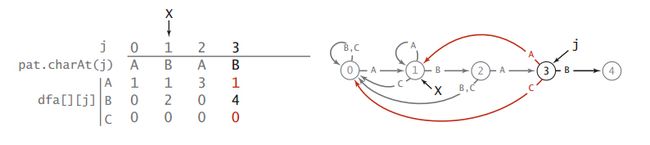
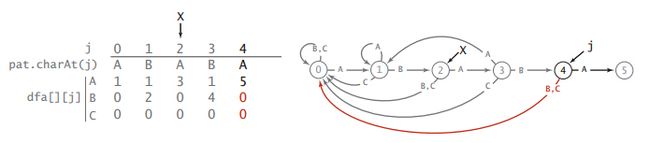
dfa[][]数组对的每一列都对应一个状态，每一行都对应一种输入。

怎么去构造一个模式对应的DFA呢？
这个过程是一个迭代的过程。
代码如下：

dfa[pat.charAt(0)][0] = 1;
for (int X = 0, j = 1; j < M; j++)
{ 
    // Compute dfa[][j].
    for (int c = 0; c < R; c++)
        dfa[c][j] = dfa[c][X];
    dfa[pat.charAt(j)][j] = j+1;

    X = dfa[pat.charAt(j)][X];
}

以上代码是：
对于每个j，
匹配失败的时候，dfa[][X]复制到dfa[][j]；
匹配成功的时候，dfa[pat.charAt(j)][j]设置为j+1；
更新X。

为什么这么做呢？
因为状态要向后面转移，必须是接收了与模式匹配的正确的字符，每次这个字符有且只有一种情况，这个字符是pat.charAt(j)。其他的字符只能使状态保持或者状态回退。

状态回退也就是让DFA重置到适当的状态，就好像回退过指针一样，但是我们不想回退指针，我们已经有了足够的信息来计算这个重启的位置。

试想一下，如果真的回退指针，我们需要重新扫描文本字符，并且这些字符就是pat.charAt(1)到pat.charAt(j-1)之间的字符（因为前面都是匹配的），忽略首字母是因为需要右移一位，忽略最后一个字符是因为上次匹配失败。
重新扫描对比过的文本字符串，直到我们的能够找到一个最长的以pat.charAt(j-1)结尾的子串，能作为模式字符串p的前缀，然后将模式字符串与这个子串的位置对齐，然后重新开始字符对比。

但是实际上，我们不需要回退指针，因为刚才的扫描过程，也是一个状态转移的过程，相当于是一个子问题。
我们把pat.charAt(1)到pat.charAt(j-1)之间的字符，一个一个输入当前的得到的DFA（因为只需要处理j-1个字符，所以当前DFA已经足够处理，相当于扫描的时候，只用模式的前一部分），到pat.charAt(j-1)的时候，会停留在一个状态，这个状态就是下一个j的状态。
这个过程利用了已经建立好的DFA的信息，进行迭代，得到新的DFA的信息，所以可以这样把整个DFA都建立起来。

模式ABABAC的DFA建立过程如下图：

这其中还有一个问题就是怎么确定复制的位置X，也就是重启的状态。
其实也很简单，就是pat.charAt(1)到pat.charAt(j-1)之间的字符能达到的最后一个状态。由于在计算DFA的过程，也是pat模式串迭代的过程，所以，在j-1的时候，我们可以把最后一个字符输入pat.chatAt(j-1)输入到当前的DFA，得到新的状态，保存起来下次继续在该状态基础上转移即可，边构造边使用。也是就是下面这行代码：

X = dfa[pat.charAt(j)][X];

到这里，KMP算法原理基本就清楚了。

《算法（第四版）》最后提到：

在实际应用中，它比暴力算法的优势并不十分明显，因为极少有应用程序需要在重复性很高的文本中查找重复性很高的模式。但该方法的一个优点是不需要再输入中回退。这使得KMP字符串查找算法更适合在长度不确定的输入流（例如标准输入）中查找进行查找，需要回退的算法在这种情况下则需要复杂的缓冲机制。

因为KMP基于DFA自动机，所以会有这样的优点，说到这里，硬件中之所以经常采用状态机进行编程，也是因为状态机不需要缓冲机制的原因，这便于高效地对输入流进行处理，比如通信中对以太网帧的解析，从MAC进来的比特流，可以很方便地通过计数等方法进行状态识别和转移，不需要接收完整个帧再进行处理，减少了缓存的消耗。

参考书目：

• 《大话数据结构》
• 《算法导论》
• 《算法（第四版）》