全球名校课程作业分享系列(3)--斯坦福计算机视觉与深度学习CS231n之softmax图像多分类

课程作业原地址：CS231n Assignment 1
作业及整理：@林凡莉 && @Molly && @寒小阳
时间：2018年1月。
出处：http://blog.csdn.net/han_xiaoyang/article/details/79138352

1. 任务

这次练习跟SVM练习类似。你将完成下面的任务：

• 通过矩阵运算为Softmax分类器实现一个损失函数
• 为这个损失函数的分析梯度实现一个完全矢量化的表达式
• 用数值梯度检查上面的分析梯度的值
• 使用验证集找到最好的学习率和正则化强度
• 用随机梯度下降法优化损失函数
• 可视化最终学习到的权重

2 知识点

2.1 Softmax分类器

Softmax分类器也叫多项Logistic回归（Multinomial Logistic Regression），它是二项Logistic回归在多分类问题上的推广。它和SVM构成了两类最常用的分类器。但跟SVM不同的是，Softmax分类器输出的结果是输入样本在不同类别上的概率值大小。我们用CS231n课件上的一张图来说明它们两者在计算上的区别：

图中的 W 为权重矩阵，假设它的大小为K*D，那么K就是类别个数，D为图像像素值大小。 xi 为图像向量， b 为偏置向量。计算

Wxi+b

得到的新向量表示图片 xi 在不同类别上的得分。上面的式子经常用

f(xi,W)

来表示，叫做得分函数（score function）。

而SVM和Softmax的一个区别在于，Softmax在得到分值向量之后还要对分值向量进行再处理，第一步是通过指数函数将分值向量映射得到新向量，第二步是对新向量进行归一化。最终得到的向量上的数值可以诠释为该图像为某类别的概率大小，而SVM得到的向量仅仅是图像在不同类别上的分值大小，没有概率的含义。
这个对分值向量处理的过程，可以用下面的函数来表示

pk=efk∑jefj

k为某个特定的类别，f为分值向量，j为任意的类别， pk 表示k类别上的概率值大小。

2.2 Softmax分类器的损失函数

既然Softmax分类器得到的输出向量为每个类别的概率值大小，我们希望正确类别对应概率值（也就是概率的对数值）越大越好，那么也就是希望概率对数值的负数，越小越好。而这个概率对数值的负数也就是我们的损失函数。下图给出了损失函数的计算公式：

虽然课件上并没说明，但Softmax的这个损失函数还有一个非常fancy的名字：交叉熵损失函数（Cross Entroy Loss），它跟最大似然估计的思想很接近。为了不增加大家的学习负担，这里就不多解释了。^_^

以上是Softmax分类器对单个图像的损失函数定义，但在实际模型的训练过程中，我们会有很多的图像，所以我们会对所有图像的损失函数求均值得到一个数据损失（data loss）。然后，为了避免出现过拟合的问题，减少模型的复杂度，我们还在损失值里加了正则项，也叫正则损失（regularization loss）。这两个损失值加起来就是训练图像的损失值：

L=1N∑iLidata loss+12λ∑k∑lW2k,lregularization loss

式子中的1／2是为了在求梯度的过程中，减少一些计算量，因为 W2 会得到 2W ,而1/2正好抵消了这里的2。

值得一提的是，在实际训练中，我们的训练集往往非常大，计算全部数据集上的损失值，然后再对其计算梯度的运算量非常大，训练速度也非常慢。所以我们经常使用随机梯度法（Stochastic Gradient Descent） 随机抽取训练集中的图像，对其进行损失值和梯度的计算来近似整个训练集的损失值和梯度。

2.3 数值梯度 vs. 解析梯度

计算梯度有两种方法：一种是缓慢的近似法（数值梯度法），实现相对简单。另一种方法（解析梯度法）计算迅速，结果精确，但实现时容易出错，且需要使用微分的知识。
数值梯度的思想就是把一个函数的定义域划分成等距的有限个数，然后通过下面的方程近似得到梯度值：

df(x)dx=limh →0f(x+h)−f(x)h

也就是说，当我们知道函数 f(x) ，并且划分的等距离间隔h也确定下来的时候，那我们就可以根据上面的公式近似得到任何一个 x 对应的梯度值（导数值）。

而解析梯度的意思是将我们的函数 f(x) 直接进行微分求导，比如将 y=x2 求导，得到的导数是 x 。这看似简单，但是当我们的函数非常复杂的时候，求导可能也会遇到比较大的问难，实现起来比较不容易。

相比之下，用数值梯度法来近似计算梯度是比较简单，但问题在于它的结果最终也只是近似，尤其是当我们把h选得很大的时候，计算的梯度值就会非常不准确。而解析梯度法用微分分析直接得到梯度的公式，用公式计算梯度速度很快，但实现的时候容易出错。所以，实际操作时常常将解析梯度法的结果和数值梯度法的结果作比较，以此来检查其实现的正确性。

接下来，我们用课堂里的例子来具体地说明一下数值梯度是如何计算得到的：

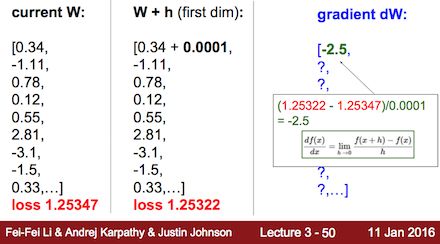
梯度dW说白了就是损失函数L对W求导得到的导数值，但因为W本来含有多个变量，所以求导结果的并不是一个数值，而是一个向量，甚至是矩阵。而导数本身的含义就是当自变量变化一个单位的时候，因变量会跟随着变化多少。在我们的例子里，梯度向量dW中的每一个值代表的是当该值对应的权重变量变化0.0001的时候，损失函数值会变化多少。具体的计算过程可以参照上图。因为对于W中的每一个权值变量都要重新计算一次损失函数值，可想而知当W中又很多变量的时候，运算量是很大的。

那解析梯度又如何计算呢？如何直接求得损失函数对W中各个变量的导数呢？这里需要用到的核心技巧就是下面的这个chain rule：

∂f∂s=∂f∂p∂p∂s

在运用这个chain rule之前，先让我们回忆下前面提到过的各个函数的数学表达式：
下面的是我们的分值函数：

fi=Wxi+b

而我们知道，在softmax里，分值需要转化成概率值，损失函数的值就是正确类别的分值所对应的负对数，下面列出公式：

pk=efk∑jefjLi=−log(pyi)

k表示某个特定的类别，i是任意图像i。

运用chain rule，我们想要得到的无非是下面这个表达式：

∂Li∂W=∂Li∂pyi∂pyi∂fk∂fk∂W

前两项的相乘的结果为：

∂Li∂fk=pk−?(yi=k)

最后一项求导的结果为

∂fk∂W=X

所以，

∂Li∂W=(pk−?(yi=k))⋅X

有兴趣的同学可以自己推导以下 ∂Li∂fk ，这个公式其实非常简洁漂亮，它的含义是，当我们有一个分值向量 f ，损失函数对这个分值向量求导的结果等于向量里每个类别对应的概率值，但除了那个正确类别的概率值，它要再减去1。例如，我们的概率向量为p = [0.2, 0.3, 0.5]，第二类为正确的类别，那么的分值梯度就为df = [0.2, -0.7, 0.5]。

而

2.4 数值稳定性问题

在实际计算中，会遇到数值稳定性（Numerical Stabiltity）的问题，因为我们的 efk 和 ∑jefj 太大了。大数之间相除很容易会导致计算结果误差很大。所以这里需要用到下面的技巧：

efk∑jefj=CefkC∑jefj=efk+logC∑jefj+logC

实践中经常把C取为 logC=−maxjfj 。也就是说，在计算损失函数之前，要把输出向量里的每个值都减去该向量里的最大值。

3 代码解析

3.1 初始化代码

#导入模块
import random 
import numpy as np 
from cs231n.data_utils import load_CIFAR10
import matplotlib.pyplot as plt
from __future__ import print_function

#调制matplotlib的画图性能
%matplotlib inline 
plt.rcParams['figure.figsize'] = (10.0, 8.0) # set default size of plots #设置默认图大小
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

#自动加载外部的Python模块
# for auto-reloading extenrnal modules
# see http://stackoverflow.com/questions/1907993/autoreload-of-modules-in-ipython 
%load_ext autoreload
%autoreload 2

3.2 加载数据

#把获取数据和数据预处理的过程封装进一个函数里
def get_CIFAR10_data(num_training=49000, num_validation=1000, num_test=1000, num_dev=500):
"""
Load the CIFAR-10 dataset from disk and perform preprocessing to prepare it for the linear classifier. These are the same steps as we used for the SVM, but condensed to a single function. 
"""

# 加载原始CIFAR-10数据
cifar10_dir = 'cs231n/datasets/cifar-10-batches-py'
X_train, y_train, X_test, y_test = load_CIFAR10(cifar10_dir)


# 从数据集中取数据子集用于后面的练习
mask = list(range(num_training, num_training + num_validation))
X_val = X_train[mask]
y_val = y_train[mask]
mask = list(range(num_training))
X_train = X_train[mask]
y_train = y_train[mask]
mask = list(range(num_test))
X_test = X_test[mask]
y_test = y_test[mask]
mask = np.random.choice(num_training, num_dev, replace=False)
X_dev = X_train[mask]
y_dev = y_train[mask]


# 数据预处理：将一幅图像变成一行存在相应的矩阵里
X_train = np.reshape(X_train, (X_train.shape[0], -1))
X_val = np.reshape(X_val, (X_val.shape[0], -1))
X_test = np.reshape(X_test, (X_test.shape[0], -1))
X_dev = np.reshape(X_dev, (X_dev.shape[0], -1))


# 标准化数据：先求平均图像，再将每个图像都减去其平均图像，这样的预处理会加速后期最优化过程中权重参数的收敛性
mean_image = np.mean(X_train, axis = 0)
X_train -= mean_image
X_val -= mean_image
X_test -= mean_image
X_dev -= mean_image


# 增加偏置的维度，在原矩阵后来加上一个全是1的列
X_train = np.hstack([X_train, np.ones((X_train.shape[0], 1))])
X_val = np.hstack([X_val, np.ones((X_val.shape[0], 1))])
X_test = np.hstack([X_test, np.ones((X_test.shape[0], 1))])
X_dev = np.hstack([X_dev, np.ones((X_dev.shape[0], 1))])

return X_train, y_train, X_val, y_val, X_test, y_test, X_dev, y_dev


# 调用该函数以获取我们需要的数据，然后查看数据集大小
X_train, y_train, X_val, y_val, X_test, y_test, X_dev, y_dev = get_CIFAR10_data()
print('Train data shape: ', X_train.shape)
print('Train labels shape: ', y_train.shape)
print('Validation data shape: ', X_val.shape)
print('Validation labels shape: ', y_val.shape)
print('Test data shape: ', X_test.shape)
print('Test labels shape: ', y_test.shape)
print('dev data shape: ', X_dev.shape)
print('dev labels shape: ', y_dev.shape)

输出结果：

Train data shape: (49000, 3073)
Train labels shape: (49000,)
Validation data shape: (1000, 3073)
Validation labels shape: (1000,)
Test data shape: (1000, 3073)
Test labels shape: (1000,)
dev data shape: (500, 3073)
dev labels shape: (500,)

我们的数据集是一个形状为（N，D）的矩阵，N代表图像的个数，D代表每个图像包含的像素值多少。而我们的标签向量则是一个一维的向量，包含N个值，对应了每一个图像的类别。

3.3 朴素版的Softmax损失函数

打开文件cs231n/classifiers/softmax.py，在softmax_loss_naive里用嵌套循环的方式实现朴素版的Softmax损失函数

#以下是插播softmax.py里的第一个代码段，详细解释参见softmax.py
num_train = X.shape[0]
num_classes = W.shape[1]
loss = 0.0
for i in xrange(num_train):
    #计算分值向量
    f_i = X[i].dot(W)
    #为避免数值不稳定的问题，每个分值向量都减去向量中的最大值
    f_i -= np.max(f_i)
    #计算损失值
    sum_j = np.sum(np.exp(f_i))
    p = lambda k: np.exp(f_i[k]) / sum_j
    loss += -np.log(p(y[i])) # 每一个图像的损失值都要加一起，之后再求均值

    # 计算梯度
    for k in range(num_classes):
        p_k = p(k)
        dW[:, k] += (p_k - (k == y[i])) * X[i]

loss /= num_train
loss += 0.5 * reg * np.sum(W * W) # 参见知识点中的loss函数公式
dW /= num_train
dW += reg*W
#插播结束

#从softmax.py加载我们刚刚写的方程
from cs231n.classifiers.softmax import softmax_loss_naive
import time # 导入time模块，之后统计函数执行时间的时候会用到


# 随机生成Softmax权重矩阵并用它来计算损失值
W = np.random.randn(3073, 10) * 0.0001
loss, grad = softmax_loss_naive(W, X_dev, y_dev, 0.0)


# 作为一个粗略的检查，我们的损失应该是一个接近-log（0.1）的值
print('loss: %f' % loss)
print('sanity check: %f' % (-np.log(0.1)))

输出结果：

loss: 2.415735
sanity check: 2.302585

随堂问题 1

为什么我们期待损失值接近-log（0.1）？

参考答案

因为我们的权重矩阵乘以0.001之后导致里面的值都非常小，接近于0，所以我们得到的分值向量里的值也都接近于0。0经过指数化接近1，因为一共有10个类别，之后的归一化会导致正确类别的概率值接近于0.1（等概论1/10），所以根据损失函数的定义得到损失值将接近-log（0.1）

3.4 梯度的代码实现

# 实现一个朴素版的Softmax损失函数，用循环嵌套的方式实现简单的梯度计算
loss, grad = softmax_loss_naive(W, X_dev, y_dev, 0.0)


# 就像我们之前在SVM做的一样，使用数值梯度检验的方法作为调试工具

# 数值梯度应接近分析梯度
# grad_check_sparse这个函数随机抽取10个位置，然后打印出该位置的数值梯度和分析梯度，以及它们之间的相对差值
from cs231n.gradient_check import grad_check_sparse
f = lambda w: softmax_loss_naive(w, X_dev, y_dev, 0.0)[0]
grad_numerical = grad_check_sparse(f, W, grad, 10)


# 就像我们之前在SVM做的一样，加入正则项再进行一次检验
loss, grad = softmax_loss_naive(W, X_dev, y_dev, 5e1)
f = lambda w: softmax_loss_naive(w, X_dev, y_dev, 5e1)[0]
grad_numerical = grad_check_sparse(f, W, grad, 10)

输出结果：

numerical: -6.081406 analytic: 0.000000, relative error: 1.000000e+00
numerical: -3.504279 analytic: 0.000000, relative error: 1.000000e+00
numerical: -2.111655 analytic: -2.111655, relative error: 9.341214e-09
numerical: 1.883857 analytic: 0.000000, relative error: 1.000000e+00
numerical: 0.457758 analytic: 0.000000, relative error: 1.000000e+00
numerical: 0.325441 analytic: 0.325441, relative error: 6.310273e-08
numerical: 1.362381 analytic: 0.000000, relative error: 1.000000e+00
numerical: -2.122575 analytic: 0.000000, relative error: 1.000000e+00
numerical: -2.317314 analytic: 0.000000, relative error: 1.000000e+00
numerical: -1.636926 analytic: 0.000000, relative error: 1.000000e+00
numerical: 3.808078 analytic: 0.002530, relative error: 9.986724e-01
numerical: 3.245057 analytic: 0.004355, relative error: 9.973196e-01
numerical: 1.398977 analytic: 0.008444, relative error: 9.880007e-01
numerical: 1.713729 analytic: -0.004240, relative error: 1.000000e+00
numerical: 1.633118 analytic: 0.000789, relative error: 9.990345e-01
numerical: -5.095081 analytic: -0.003568, relative error: 9.986005e-01
numerical: -0.393176 analytic: -0.004208, relative error: 9.788203e-01
numerical: 1.841963 analytic: -0.004583, relative error: 1.000000e+00
numerical: -1.541853 analytic: -0.004422, relative error: 9.942810e-01
numerical: 1.318521 analytic: 0.003875, relative error: 9.941396e-01

3.5 向量版的Softmax损失函数

我们已经有了一个朴素版的softmax损失函数及其梯度的实现，现在在softmax_loss_vectorized函数中再实现一个向量版的函数。这两个函数的结果应该是一样的，只是向量版的速度运算速度会快很多。

#插播softmax.py里的第二个函数段
num_train = X.shape[0]
f = X.dot(W)
f -= np.max(f, axis=1, keepdims=True) 
sum_f = np.sum(np.exp(f), axis=1, keepdims=True)
p = np.exp(f)/sum_f

loss = np.sum(-np.log(p[np.arange(num_train), y]))

ind = np.zeros_like(p)
ind[np.arange(num_train), y] = 1
dW = X.T.dot(p - ind)

loss /= num_train
loss += 0.5 * reg * np.sum(W * W)
dW /= num_train
dW += reg*W
#插播结束

可以看到向量版里不再包含循环和嵌套，代码更简洁和清爽。

tic = time.time() # 函数执行前的时间，以浮点数的形式存储在tic中
loss_naive, grad_naive = softmax_loss_naive(W, X_dev, y_dev, 0.000005)
toc = time.time() # 函数执行完毕的时间，同样是浮点数
print('naive loss: %e computed in %fs' % (loss_naive, toc - tic)) # 打印出函数softmax_loss_naive的执行时间

from cs231n.classifiers.softmax import softmax_loss_vectorized
tic = time.time()
loss_vectorized, grad_vectorized = softmax_loss_vectorized(W, X_dev, y_dev, 0.000005)
toc = time.time()
print('vectorized loss: %e computed in %fs' % (loss_vectorized, toc - tic)) # 打印出函数softmax_loss_verctorized的执行时间

# As we did for the SVM, we use the Frobenius norm to compare the two versions of the gradient.
# 正如我们在SVM做的一样，利用弗罗贝尼乌斯范数（Frobenius norm）来比较这两个版本的梯度

grad_difference = np.linalg.norm(grad_naive - grad_vectorized, ord='fro')
print('Loss difference: %f' % np.abs(loss_naive - loss_vectorized)) # 打印出两个函数返回的损失值之间的差值
print('Gradient difference: %f' % grad_difference) #打印出两个函数返回的梯度之间的距离

输出结果：

naive loss: 2.390404e+00 computed in 0.135962s
vectorized loss: 2.390404e+00 computed in 0.015693s
Loss difference: 0.000000
Gradient difference: 0.000000

从输出结果中可以看出向量版的函数计算速度要快很多。但是得到的损失值和梯度梯度并没有差别。

3.6 超参数调优

# 利用验证集来微调超参数（正则化强度和学习率），你应该分别使用不同的数值范围对学习率和正则化强度进行微调。如果足够细心，你应该能在验证集上实现高于0.35的分类准确率。

from cs231n.classifiers import Softmax
results = {}
best_val = -1
best_softmax = None
learning_rates = [1e-7, 5e-7]
regularization_strengths = [2.5e4, 5e4]
learning_rates = np.logspace(-10, 10, 10) 
regularization_strengths = np.logspace(-3, 6, 10) # 使用更细致的学习率和正则化强度


# 用验证集来调整学习率和正则化强度；这跟你在SVM里做的类似；把最好的Softmax分类器保存在best_softmax里
iters = 100
for lr in learning_rates:
    for rs in regularization_strengths:
    softmax = Softmax() # 函数代码在linear classifier文件里
    softmax.train(X_train, y_train, learning_rate=lr, reg=rs, num_iters=iters)

y_train_pred = softmax.predict(X_train)
acc_train = np.mean(y_train == y_train_pred)
y_val_pred = softmax.predict(X_val)
acc_val = np.mean(y_val == y_val_pred)

results[(lr, rs)] = (acc_train, acc_val)

    if best_val < acc_val:
       best_val = acc_val
       best_softmax = softmax 
################################################################################
# END OF YOUR CODE #
################################################################################
# Print out results.
#打印结果
for lr, reg in sorted(results):
    train_accuracy, val_accuracy = results[(lr, reg)]
    print('lr %e reg %e train accuracy: %f val accuracy: %f' % (lr, reg, train_accuracy, val_accuracy))

print('best validation accuracy achieved during cross-validation: %f' % best_val)

输出结果（只是截取了部分结果）：

lr 1e-10 reg 0.001 train accuracy: 0.0994897959184 val accuracy: 0.107
lr 1e-10 reg 0.01 train accuracy: 0.120816326531 val accuracy: 0.107
lr 1e-10 reg 0.1 train accuracy: 0.0834897959184 val accuracy: 0.08
lr 1e-10 reg 1.0 train accuracy: 0.0955306122449 val accuracy: 0.095
lr 1e-10 reg 10.0 train accuracy: 0.111448979592 val accuracy: 0.118
lr 1e-10 reg 100.0 train accuracy: 0.109367346939 val accuracy: 0.103
lr 1e-10 reg 1000.0 train accuracy: 0.114530612245 val accuracy: 0.092
lr 1e-10 reg 10000.0 train accuracy: 0.0947755102041 val accuracy: 0.103
lr 1e-10 reg 100000.0 train accuracy: 0.118653061224 val accuracy: 0.12
lr 1e-10 reg 1000000.0 train accuracy: 0.120489795918 val accuracy: 0.129
lr 1.6681005372e-08 reg 0.001 train accuracy: 0.0967755102041 val accuracy: 0.091
lr 1.6681005372e-08 reg 0.01 train accuracy: 0.116183673469 val accuracy: 0.129
lr 1.6681005372e-08 reg 0.1 train accuracy: 0.076 val accuracy: 0.076
lr 1.6681005372e-08 reg 1.0 train accuracy: 0.0948367346939 val accuracy: 0.094
lr 1.6681005372e-08 reg 10.0 train accuracy: 0.0985510204082 val accuracy: 0.109
lr 1.6681005372e-08 reg 100.0 train accuracy: 0.101040816327 val accuracy: 0.097
lr 1.6681005372e-08 reg 1000.0 train accuracy: 0.121510204082 val accuracy: 0.098
lr 1.6681005372e-08 reg 10000.0 train accuracy: 0.110142857143 val accuracy: 0.129
lr 1.6681005372e-08 reg 100000.0 train accuracy: 0.0807346938776 val accuracy: 0.078
lr 1.6681005372e-08 reg 1000000.0 train accuracy: 0.0935102040816 val accuracy: 0.1
best validation accuracy achieved during cross-validation: 0.208

3.7 测试结果以及准确率计算

# 在测试集上验证我们得到的最好的softmax分类器
y_test_pred = best_softmax.predict(X_test)
test_accuracy = np.mean(y_test == y_test_pred)
print('softmax on raw pixels final test set accuracy: %f' % (test_accuracy, ))

输出结果：

softmax on raw pixels final test set accuracy: 0.216000

3.8 可视化结果

# 可视化学习到的每一个类别的权重
w = best_softmax.W[:-1,:] # 出去偏置项
w = w.reshape(32, 32, 3, 10)

w_min, w_max = np.min(w), np.max(w)

classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
for i in range(10):
    plt.subplot(2, 5, i + 1)

# 将权重重新变成0-255中间的值
wimg = 255.0 * (w[:, :, :, i].squeeze() - w_min) / (w_max - w_min)
plt.imshow(wimg.astype('uint8'))
plt.axis('off')
plt.title(classes[i])