学习理论、模型选择、特征选择——斯坦福CS229机器学习个人总结（四）

这一份总结里的主要内容不是算法，是关于如何对偏差和方差进行权衡、如何选择模型、如何选择特征的内容，通过这些可以在实际中对问题进行更好地选择与修改模型。

1、学习理论（Learning theory）

1.1、偏差/方差（Bias/variance）

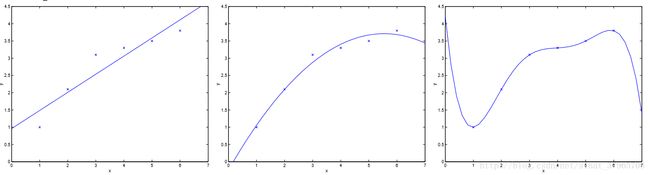
图一
对一个理想的模型来说，它不关心对训练集合的准确度，而是更关心对从未出现过的全新的测试集进行测试时的性能，即泛化能力（Generalization ability）。
有的模型用在用一个样本集训练过后，再用同一个样本集做预测，这样得到的模型的准确率非常高。但是，当用这个模型去预测新的数据的时候，效果却非常不理想。这就是泛化能力弱的表现，这样的模型非常容易过拟合。

图一最左边的图，用线性模型去拟合一个二次模型，无论该训练集中有多少样本，都会不可避免地出现较大的误差，这种情况被称为欠拟合，对应着高偏差；
图一最右边的图，用高次模型去拟合一个二次模型，虽然它能够让图中每个样本点都经过该曲线，但是对于新来的数据可能会强加上一些它们并不拥有的特性（一般是训练样本带来的），这会让模型非常的敏感，这种情况被称为过拟合，对应着高方差。

如何选择一个模型使得它在偏差与方差之间取得一个平衡，是学习理论要解决的问题。在下面“一致收敛的推论”一节中，会得到一个用来权衡偏差、方差的公式，接下来会从头开始推导这个公式。

1.2、准备知识

开始推导之前要先把一些准备知识提出来，这样从“一致收敛”中开始的推导会很顺利。

联合界引理（The union bound）

引理：令 A1,A2,⋯,Ak 是k个事件，组合成k集，它们可能相互独立，也可能步相互独立，对此，我们有：

P(A1∪⋯∪Ak)≤P(A1)+⋯+P(Ak)(1)

它要表达的意思是“K集事件之一发生的概率最多是K集发生的概率之和”。
比如当 P(A1∪⋯∪Ak)=P(A1) ，它的概率最多是K集发生的概率之和。

霍夫丁不等式（Hoeffding inequality）

引理：令 Z1,Z2⋯,Zm 为m个独立同分布事件，它们都服从伯努利分布，则有:

P(Zi=1)=ϕ,P(Zi=0)=1−ϕ

并用 Zi 的平均值来得到一个 ϕ 的估计值 ϕ^ ：

ϕ^=∑mi=1Zim(2)

接着对于任意的固定值 γ>0 ，存在：

P(∣∣ϕ−ϕ^∣∣>γ)≤2exp(−2γ2m)(3)

以上就是霍夫丁不等式，也称为切尔诺夫界（Chernoff bound）。
这个定理的意义在于，随着 m 的增长，右式的指数会持续下降，左式中对参数 ϕ^ 的估计会越来越接近真实值 ϕ （画个 e−x 的图像就知道了）。

经验风险最小化（Empirical risk minimization）

下面以二分类问题进行说明。
给定一个训练集 S{(x(i),y(i));i=1,2,⋯,m} ， (x(i),y(i)) 是服从概率分布 D 的独立同分布变量，那么对于一个假设 h ，我们将假设 h 的训练误差（Training error）——也称为经验风险（Empirical risk）或者是经验误差（Empirical error）——定义为：

ε^=1m∑i=1mI{h(x(i))≠y(i)}(4)

它表示：在训练样本中，用假设 h 进行分类，分类失败数占总数的百分比。注意它在表示上 有带帽符号。

相对应的有一般风险，也称为一般误差（Generalization error）：

ε=PD(h(x)≠y)(5)

PD 表示 (x,y) 服从 D 分布。
式（5）表示：实际分类中，使用了假设 h 进行分类，样本不服从 D 分布的概率。它在表示上 无带帽符号。

在我的理解中，训练误差是训练中产生的误差，一般误差是实际预测、分类中产生的误差。接下来的推导中它们会一直出现，可能会搞混，要一直理解到它们的意思才行。

假设模型集合为：

H={hθ:hθ(x)=I{θTx≥0},θ∈Rn+1}(6)

集合 H 中，每一个成员都是一个假设函数 h ，且它们都是线性分类器。

由式（4）经验风险的形式化定义，有经验风险最小化（简称ERM）为：

θ=argminθε^(hθ)(7)

它表示：选择一个参数 θ ，它所对应的假设函数 h ，使得经验风险最小。

还有另外一种ERM的等价表示方法，其ERM的定义为：

h^=argminh∈Hε^(h)(8)

它表示：选择一个假设函数 h ，使得经验风险最小。

1.3、一致收敛（Uniform convergence）

此处的一致收敛有两个前提。一是由第二种ERM推导，二是式（6）中假设函数的数量是有限的情况下的。
一致收敛的意义是：训练误差与一般误差的差值大于某阈值的概率存在着上界。还有一点扩展就是这个上界会因样本数量的上升而急速下降。由一致收敛我们可以推导出偏差/方差权衡的方式。

首先，假设类的集合 H={h1,h2,⋯,hk} ，它的成员数量是有限的，为k。
其次，用 Zj=I{hi(x(j))≠y(j)} 表示，假设类 hi 把样本 ((x(j)),y(j)) 错误分类了。
于是我们有假设类 hi 的训练误差：

ε^(hi)=1m∑j=1mZj(9)

由式（3）的霍夫丁不等式，我们令训练误差 ε^(hi)=ϕ^ ，令一般误差 ε(hi)=ϕ ,有：

P(|ε(hi)−ε^(hi)|>γ)≤2exp(−2γ2m)(10)

这表示当 m 很大的时候，假设类 hi 的训练误差和一般误差是很接近的。
但是仅仅证明了这个还不够，我们要证明所有属于集合 H 的假设类都满足上面这个结论。
接下来我们用 Ai 表 |ε(hi)−ε^(hi)|>γ ，则有：

P(Ai)≤2exp(−2γ2m)(11)

如果存在一个假设类使得其一般误差很大，但是存在着上界，这个上界是由 P(A1∪⋯∪Ak) 决定的：

P(∃h∈H.|ε(hi)−ε^(hi)|>γ)=P(A1∪⋯∪Ak)(12)

使用式（1）的联合界定理与式（11）的假设，我们有如下推导：

P(∃h∈H.|ε(hi)−ε^(hi)|>γ)=P(A1∪⋯∪Ak)≤∑i=1kP(Ai)≤∑i=1k2exp(−2γ2m)=2kexp(−2γ2m)(13)

再用1减去式（13）的左右两侧，得到：

1−P(∃h∈H.|ε(hi)−ε^(hi)|>γ)=P(∀h∈H.|ε(hi)−ε^(hi)|≤γ)≥1−2kexp(−2γ2m)(14)

式（14）即为一致收敛定理：对于所有属于集合 H 的假设类 h ，至少存在 1−2kexp(−2γ2m) 的概率，使得训练误差与一般误差的差值最大为 γ 。它暗示了当 m 很大的时候，训练误差会收敛到一般误差。

1.4、一致收敛的推论与偏差/方差权衡（Bias/variance tradeoff）

一致收敛的推论

一致收敛中，有三个参数，分别是样本数量 m ，误差阈值 γ ，以及误差概率。
当固定了 m,γ ，我们得出了概率，推导出了一致收敛的结论。下面对剩下的两个参数关联进行说明。

给定误差阈值 γ 与一个 δ>0 ，需要多大的样本数量，才能保证至少有有 1−δ 的概率，使得训练误差与一般误差的差值在 γ 之内？
令 δ=2kexp(−2γ2m) 并对 m 求解，就能得到：

m≥12γ2log2kδ(15)

（对于这个 ≥ 号我没想明白，如果把式（15）倒推的话，有 δ≥2kexp(−2γ2m) ，我不知道取这个符号的根据是什么。但是只有这样，这里的 m 以及下文的 γ 在推导上才能顺利地进行。如果有朋友可以告知，不胜感激。）
这个推论的意义是：当一个算法或者模型想要到达一个确定的性能的时候，它所需要的样本数目。这也称为算法的样本复杂度（Sample complexity）。

再看另一个。给定样本数量 m 与 δ ，至少有 1−δ 的概率，误差阈值会落在什么范围内？沿用上面的不等号方向，有：

γ≤12mlog2kδ−−−−−−−−−√(16)

可以进一步得到：

|ε(h)−ε^(h)|≤γ≤12mlog2kδ−−−−−−−−−√(17)

这被称为误差界（Error bound）。

偏差/方差权衡

由经验风险最小化公式，我们有如下定义。
使训练误差最小的函数 h^ ：

h^=argminh∈Hε^(h)(18)

使 一般误差最小的函数 h∗ ：

h∗=argminh∈Hε(h)(19)

注意有带帽符号的 ε^(h) 表示训练误差，无带帽符号的 ε(h) 表示一般误差。

下面，由式（17）一致收敛定理的应用，把 h^ 带入 h ，我们得到：

ε(h^)≤ε^(h^)+γ(20)

看向式（18）与式（19）， h^ 与 h∗ 均是集合 H 的成员。对于训练误差——函数 ε^(h) 来说， h^ 对它取最小值，集合 H 中的其他任何一个取值都不会使函数 ε^(h) 更小了，包括 h∗ （ h∗ 使一般误差 ε(h) 最小，但这是区别于训练误差 ε^(h) 的另外一个函数了）。
通过这些分析我们有 ε^(h^)≤ε^(h∗) ，对于式（20）右边的式子有下一步推导：

ε^(h^)+γ≤ε^(h∗)+γ(21)

类似地，我们再使用一次式（17）的一致收敛定理，这次我们把 h∗ 带入 h ，有：

ε^(h∗)≤ε(h∗)+γ(22)

把式（22）与式（20）、式（21）连接起来，就得到了：

ε(h^)≤ε^(h^)+γ≤ε^(h∗)+γ≤ε(h∗)+2γ(23)

ε(h^) 表示，经过经验风险最小化处理得到的最优假设函数 h^ ，在实际应用 ε(h) 中的分类错误率。
式（23）表示，在一致收敛成立的前提下，实际应用中，训练最优（ERM）与理论上能达到的最优之间，错误率最多相差2 γ 。

把式（19）与式（16）代入式（23），能得到下面的定理。
令 |H|=k ，固定任意的 m,δ ，那么至少有 1−δ 的概率，有：

ε(h^)≤(minh∈Hε(h))偏差衡量+212mlog2kδ−−−−−−−−−√方差衡量(24)

这就是偏差、方差权衡的公式。 ε(h^) 表示实际分类错误率，越小越好。
当选择一个较复杂的模型时， |H|=k 的值会变大，这表示假设类的选择变多了，在上式“偏差衡量”一项中，将会有更多的假设类可以选择，在这些更多的选择中，大概率会出现使 ε(h) 更小的假设类，对应着错误率降低；
与此同时， k 正比于“方差衡量”一项， k 值的增大，将会使方差增大，对应着错误率提高。
这就把欠拟合高偏差、低方差的特点，以及过拟合低偏差、高方差的特点，用公式表达出来了。
选择一个假设类，使得偏差、方差之和最小，才能得到一个好的模型。

还有一个推论：令 |H|=k ，固定任意的 m,δ ，那么至少有 1−δ 的概率使 ε(h^)≤ε(h∗)+2γ 成立的前提是：

m≥12γ2log2kδ=O(1γ2logkδ)(25)

1.5、VC维（VC dimension）

关于VC维有如下两个定义。
定义一：给定一个集合 S={x(i),⋯,x(d)} ，当对于集合 S 的任何一种标记方式，模型集合 H 中总存在着某个假设 h ，可以将其线性分开，则称 H 可以分散 S 。
定义二：对一个模型集合来说，它的VC维，记为 VC(H) ，是其能够分散的最大集合的大小。
下面举一个具体的例子。

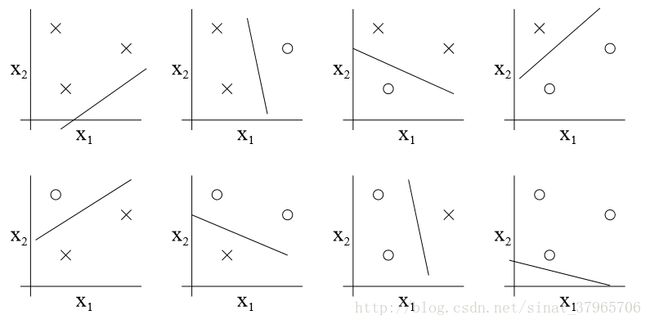
图二
图二中， S={x(1),x(2),x(3)} ，上面每一个图都对应着 S 的一种标记方式，共8种，而每一种标记方式都有对应的直线（模型集合 H 中某个假设类 h ）将其线性分开。
虽然有这种情况：三个点正好在同一条直线上，或者三个点重合了，此时是没有直线能够将它们线性分开的；但是只要存在着以任何方式标记的三个点的集合，能被直线集合线性分开，它就满足定义一。
所以我们称线性模型集合 H 可以打散三个点的集合 S ，并且 H 的VC维是3，即 VC(H)=3 。
更一般地，对于 n 维线性分类模型来说，它的VC维为 n+1 。

对于一个模型集合来说，不管它是有限的还是无限的，都可以根据VC维来获得其一致收敛定理。这里直接给出结论（Ng在课上说，他在读博期间花了一个星期的时间，每天早9晚6一直在看，才看明白VC维证明过程，所以课上也没有给出证明）。
定理：对于模型集合 H ，令 d=VC(H) ，那么至少有 1−δ 的概率，对于模型集合中所有的 h 来说，有：

|ε(h)−ε^(h)|≤O(dmlogmd+1mlog1δ−−−−−−−−−−−−−−−−√)(26)

类似地，有偏差、方差权衡：

ε(h^)≤ε(h∗)+O(dmlogmd+1mlog1δ−−−−−−−−−−−−−−−−√)(27)

引理：为使 ε(h)−ε^(h)≤γ 对模型集合 H 中的所有 h ，都有至少 1−δ 的概率成立，那么样本数量必须满足：

m=Oγ,δd(28)

一般性的说法是： 为了使模型达到较好的效果，需要的样本数必须与模型的VC维在同一数量级。

2、模型选择——交叉验证（Model selection）

对于同一个问题，可以以有多种模型来解决。如一个分类问题，可以用logistic回归、SVM、朴素贝叶斯等，那么如何选择一个最好的模型呢。
首先会想到的是，对每个模型，用训练集合去训练他们，取训练误差最小的模型。
但是这有明显的缺陷，因为这将会得到一个最复杂的模型（比如一个10次多项式），产生严重的过拟合。
下面提供一些选择模型的标准方法。

保留交叉验证（Hold-out cross validation）

保留交叉验证也称为简单交叉验证（Simple cross validation），做法如下：
（1）把训练集合随机分成 Strain （如训练集合的70%）与 Stest （如训练集合的30%）
（2）在 Strain 上训练模型
（3）在 Stest 上做测试
（4）选择测试误差最小的模型

k重交叉验证（k-fold cross validation）

有些情况下样本来之不易，比如一些代表着苦痛的临床病例，如果使用上面的简单交叉验证，资源存在着一定的浪费，所以稍作改进就得到了K重交叉验证法：
（1）把样本随机分成k份
（2）留下第1份作为测试集，在其他 k−1 份上训练模型
（3）留下第2份作为测试集，在其他 k−1 份上训练模型
⋮
（n）留下第k份作为测试集，在其他 k−1 份上训练模型
（n+1）选择测试误差最小的模型
这样，训练与测试结束后，样本集中的每一个样本都会产生自己的分类结果。
常见的做法是取 k=10 。

留一验证法（Leave-one-out cross validation）

为了使样本能够作为训练集合更充分地在每一次训练中被使用，还有一种留一验证法，即令 k=m ，意思是在整个样本集中只留下一个样本进行测试，其他全部用来训练模型。做法与上面的K重交叉验证法一样，是它的一个极端。

3、特征选择（Feature selection）

对于一些机器学习问题，可能会遇到非常高维的特征空间，输入特征向量的维数可能非常高，像文本分类问题，特征值很容易就达到了30000-50000个，在如此高维的特征下，模型很容易过拟合，如果可以减少特征的数量，就可以减小算法的方差，从而降低过拟合的风险，对于文本分类的问题，可能只有少数相关特征，能对文本分类起到较大的作用。如“like”、“a”、“the”、“of”这样的单词，对于判断一个邮件是否是垃圾邮件没有帮助。
如何选择与学习算法真正相关的特征，减少与学习内容无关或者影响不大的特征，从而降低VC维，得到更为有效的模型？下面将会提供几种特征选择算法。

前向选择法（Forward search）

前向选择法步骤如下：
①初始化若干特征为特征子集 F=Φ
②对不属于 F 的每个特征，计算添加该特征后模型精度的提升
③选择提升最大的特征
④重复第②步与第③步，直到收敛
收敛的判断依据有，达到预期的一般误差，或者是精度不再上升。

根据前向选择法，我们容易得到后向选择法（Backward search）：初始化全部特征，每次减少一个特征计算下降的精度，去掉精度下降最不大的的特征。

特征过滤法（Filter feature selection）

前后选择法可以达到较优的特征选择结果，但是它要反复训练模型，计算量很大，尤其是样本数据很大的时候。为了使特征选择更简单，这里提出了一个更简单的特征选择方法——特征过滤法，相比起前后向选择法，它的计算量非常小。

特征过滤法的思路是，计算每一个特征 xi 与标签 y 的相关性，得到每个特征的评分，从而选择出与标签 y 最相关的特征。
得到每个特征的评分之后，使用多少个特征才能可以让模型的效果最好呢？标准的方法还是采用交叉验证，排序选出 k 个最有效特征。
下面是获取评分的两个方式。

互信息（Mutual information,MI）方式，当 xi 是离散型变量的时候，MI的计算方式如下：

MI(xi,y)=∑xi∈{0,1}∑y∈{0,1}p(xi,y)logp(xi,y)p(xi)p(y)(29)

其中 p(xi,y) 等是概率，可以在训练集合中统计得到结果。

KL（Kullback-Leibler）距离方式：

MI(xi,y)=KL(p(xi,y)||p(xi)p(y))(30)

KL距离的作用是衡量分布之间的差异，关系越强KL距离越大，反之比如当 xi 与 y 相互独立时，KL距离为0。

贝叶斯正则化

前面的特征选择算法都是直接消减特征，使得模型变得更简单，防止过拟合。接下来会介绍另外一种防止过拟合的方法，它会保留所有的特征，这个方法被称为正则化（Regularization）。

在之前的讲述中，求参数时一般使用最大似然估计法：

θML=argmaxθ∏i=1mp(y(i)∣x(i);θ)(31)

θ 之前用的是分号，表示 θ 是一个固定的参数，可以通过统计学的方法求解出来。这是统计学派的观点。

在统计学中，还有另外一个学派，称为贝叶斯派，他们认为 θ 是一个随机变量，服从某个先验分布。他们对参数 θ 的最大后验概率（Maximum a posterior,MAP）估计的方式是：

θMAP=argmaxθ∏i=1mp(y(i)∣x(i),θ)p(θ)(32)

上式即为正则化方式。与式（31）相比， θ 之前是一个逗号，表示 θ 是一个变量，并且后面乘上了一个先验概率 p(θ) ，表示这个变量 θ 服从它的分布（在这里 p(θ) 是高斯分布）。
这样一来我们预测的时候，使用的模型就是（以线性回归为例）：

hθMAP(x)=θMAPx(33)

注意在这个模型后面是带有一个 θ 的高斯分布的。我们可以想象，在高斯分布中，大多数的点的值都在0附近，当我们乘上这么一个先验概率的时候，很多特征值就会被乘上一个很接近0的数值。如此一来，尽管所有的特征都还保留，但是它们对于模型的作用微乎其微，几乎可以忽略到当它不存在。实际上前面直接删除特征的方式，等同于正则化时将该特征对应的 θ 分量乘上0。

不知道是中西方思维的不同还是个人原因，讲义上的内容有时候会给我一种反过来推导的感觉。正常来说，应该是由一些公理A带着问题出发，从A开始推到B，然后B推到C，C推到D，如此下去，一步一步皆有迹可循；但是讲义中多处出现这种情况：因为D要被C使用，所以直接给出了D，再从虚空中拿出C、或者从别的什么地方推导出C，然后说C是怎么使用D的（B和A也一样）。这就给人一种思维上断层的感觉，难有引导的作用，虽然最后看懂了会感到整个讲述的东西还是清晰的，但是在一开始完全不理解的情况下从头看下来、理解下来的过程实在是太痛苦了。

4、实际应用中的一些问题

Ng在前面先给出了一些忠告：避免过早优化以及局部优化，因为这样做很可能无法使系统性能得到提升，让很多时间被白白浪费掉。

如何进行ML算法诊断？

①判断算法存在高方差还是高偏差
高偏差：模型本身不合适——需要更多、更好的特征增加模型的复杂度。
高方差：过拟合问题——减少特征数量，降低VC维；或者增加样本数量，使训练更充分。

②目标（损失）函数是否正确（下面用 J 表示损失函数）
J(算法)>J(实际) ：令损失函数更收敛（多迭代几次梯度下降/牛顿法）。
J(算法)<J(实际) ：损失函数错误，不能反映真实需要，需对其本身进行改进。

误差分析与销蚀分析

①误差分析
一个系统由各个部件组成，对每个部件用基准值代替算法输出，观察性能变化，取得性能提升最多的部件，对该部件进行优化。

②销蚀分析
做一个初始分类容器，将部件逐个剔除，观察性能的下降幅度，去掉无下降或者下降少的特征。

注意：以上两种方法都需要注意增减特征部件的顺序，因为它们的效果是累积的，顺序不同会有相应的影响。

如何开始一个ML问题的研究

①研究新算法时——仔细构建：深入分析->提取特征->构建算法
②工程应用型——创建->修改法：创建一个较差的系统->诊断->修改->诊断->修改……
③分析数据：对样本数据的理解、预处理很重要
④着眼于真正有用的关键问题
⑤三分之一到一半的时间花在诊断上都是可以接受的