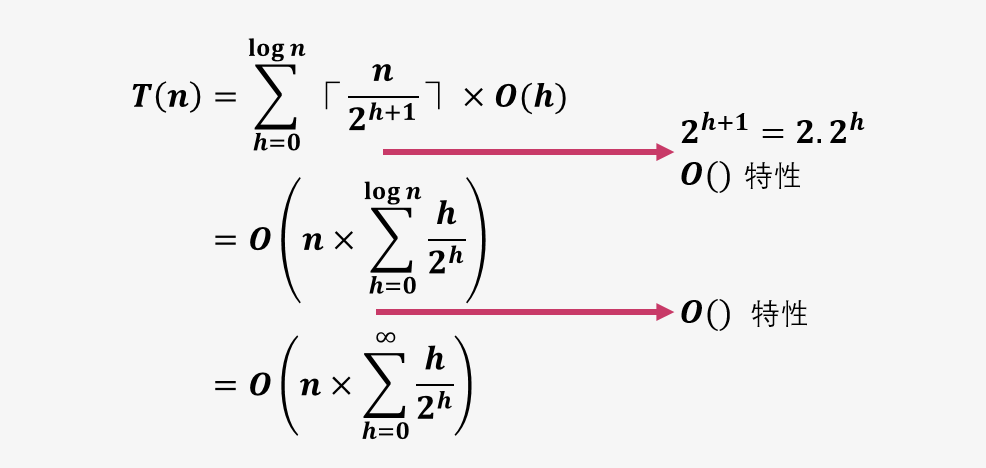图解:什么是堆排序?
二叉堆(Binary Heap)是一颗特殊的完全二叉树,一般分为大顶堆和小顶堆,我就不啰嗦啦!具体内容你可以看一下 图解:什么是二叉堆?
堆排序
要学习今天的堆排序(Heap Sort),我们以一个数组 arr = [5、1、4、2、8、4] 开始(这个数组我们之前讲排序算法常用的):
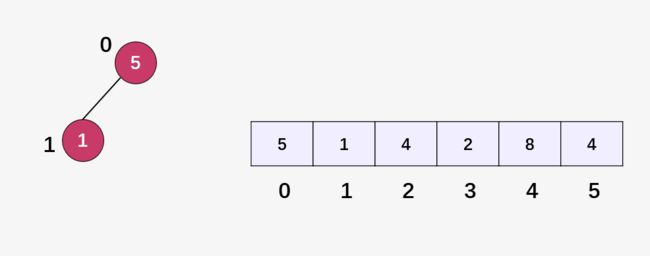
我们首先以这个数组建立一个大顶堆,插入结点 5 作为根结点:
然后将结点 1 插入到最后一个位置,也就是结点 5 的左孩子,1 < 5 ,满足大顶堆的属性:
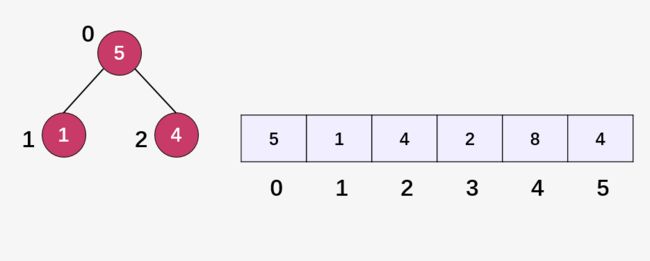
将结点 4 插入到最后一个位置,即结点 5 的右孩子 ,又因为 4 < 5 ,满足大顶堆的属性,不需要进行调整:
将结点 2 插入到最后一个位置,即结点 1 的左孩子位置,但是此时不满足大顶堆的属性(插入结点 2 小于其父结点 1 的值),所以交换两者的值;此时并未结束,继续判断此时插入结点 2 与当前父结点 5 的大小关系,发现 2 < 5 ,满足大顶堆的属性,结束判断。这个过程就是二叉堆的插入操作:
紧接着将结点 8 插入到最后一个位置,即结点 2 的右孩子位置,此时不满足大顶堆的属性(插入结点 8 小于其父结点 2 ),故交换两者位置;然后继续向上修正,判断当前结点 8 与其父结点 5 的大小关系,8 > 5 (不满足大顶堆的属性),交换两者位置,继续修正,发现结点 8 已为树的根结点,修正结束:
最后,我们将结点 4 插入到最后一个位置,即结点 4(下标为2) 的左孩子位置,且其值小于等于父结点,故不进行修正:
以上算是对于二叉堆插入操作的一个回顾,建堆的过程(这里是按照插入操作进行建堆的),接下来才是堆排序的核心操作。
设 表示堆中的元素个数,对数组 arr = [8,5,4,1,2,4] 而言, ;
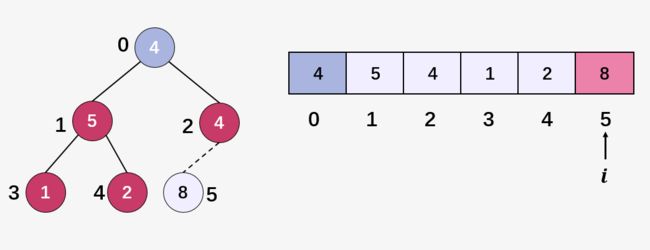
第一步:将堆顶的元素 8 (即数组 arr[0] ,最大元素)的元素与堆的最后一个元素 4(即数组当中的最后一个元素 4 )交换,此时就相当于选择出了数组当中的最大元素,将其从堆中去掉:
第二步:从结点 4 (下标为 0 )开始进行 堆化(Heapify)操作,这里我们只啰嗦一次奥!计算结点 4 (下标为 0 )的左孩子 (即结点 5 ),右孩子 (即结点 4),比较三者的大小,发现 5 > 4 违反了堆的性质,交换 5 和根结点 4 ;然后继续对结点 4 (下标为 1 )进行判断,发现其左孩子 1 和右孩子 2 均小于 4 ,堆化结束。
第三步:将堆顶元素 5 (下标为 0)和当前最后一个元素 2 (即 i 指向的位置)交换, 此时就相当于选择出了数组当中的次最大元素,将其从堆中去掉:
第四步:从当前的堆顶元素 2 开始进行堆化操作,交换 2 (下标 0)和其左孩子 4 (下标 1),为什么不是右孩子 4 (下标 2)呢?因为我们在堆化的时候,优先和左孩子进行了对比,只有当右孩子大于左孩子的情况下,才考虑将右孩子与其父结点交换,堆化后的结果如下图所示:
第五步:交换根结点 4 和最后一个结点 1 ,从堆中去掉结点 4 (下标 3):
第六步:从根结点 1 开始进行堆化操作,交换了根结点 1 和 4 (下标 2):
第七步:交换根结点 4 和 1 ,从堆中去掉结点 4 :
第八步:从根结点 1 开始进行堆化操作,交换了结点 2 和 1 :
第九步:交换根结点 2 和最后一个元素 1 ,将结点 2 从堆中去掉:
第十步:发现堆中仅剩余一个元素,堆排序结束,我们看到原始的输入数组 arr = [5、1、4、2、8、4] 变成了有序数组 arr = [1、2、4、4、5、8] 。
这就是有趣有好玩的堆排序,其本质上是对二叉堆的一个应用。
我们都知道选择排序是利用线性的时间复杂度 遍历数组,每一趟选择出数组当中最大的元素,总共选择 趟,所以选择排序的时间复杂度为 。
而堆排序事实上就是对选择排序的一个优化,本来用 的时间才能选择出数组中最大或最小元素,借助于大顶堆和小顶堆数据结构,就可以将这个选择操作的时间复杂度降到 ,同样是选择 趟,所以堆排序的时间复杂度为 量级。
不难发现,堆排序是一个基于比较的排序算法,且在排序过程中由于要进行堆化操作(不断交换)(Heapify),而造成其不稳定性,所以堆排序是一个不稳定的排序算法。
实现代码
只要会写二叉堆的堆化操作,看堆排序的代码会相当简单。
public class HeapSort
{
public void heapSort(int arr[])
{
int n = arr.length;
//建堆(你也可以考虑进行上面的插入操作)但是这里调用的是Heapify
//可以达到同样的建堆效果
for (int i = n / 2 - 1; i >= 0; i--){
heapify(arr, n, i);
}
//从堆中一个一个地选择出最大元素
for (int i = n-1; i > 0; i--)
{
// 交换堆的根结点(最大元素)与当前最后一个元素(i)
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
// 在去掉最后一个元素的堆上进行堆化操作
heapify(arr, i, 0);
}
}
// 堆化操作
void heapify(int arr[], int n, int i)
{
int largest = i; // 初始化最大元素为根结点
int l = 2*i + 1; // i 的左孩子结点 left = 2*i + 1
int r = 2*i + 2; // i 的右孩子结点 right = 2*i + 2
// 如果左孩子结点比根结点大,更新largest为左孩子
if (l < n && arr[l] > arr[largest])
largest = l;
// 如果右孩子比最大元素大,更新largest为右孩子
if (r < n && arr[r] > arr[largest])
largest = r;
// 如果最大元素不是根结点,进行交换操作并递归调用Heapify
if (largest != i)
{
int swap = arr[i];
arr[i] = arr[largest];
arr[largest] = swap;
// 对由于交换操作受到影响的子树递归调用Heapify
heapify(arr, n, largest);
}
}
public static void main(String args[])
{
int arr[] = {5,1,4,2,8,4};
int n = arr.length;
HeapSort ob = new HeapSort();
ob.sort(arr);
for(int i = 0; i < n; i++){
System.out.print(arr[i] + ",")
}
}
}
请注意:上面代码中的建堆操作代码
for (int i = n / 2 - 1; i >= 0; i--){
heapify(arr, n, i);
}
如果看这个代码感觉不舒服,没关系,我们用更香的方式来一遍。我们还是以数组 arr = [5、1、4、2、8、4] 为例说明这种建堆方式。
与插入操作建堆不同的是(插入操作建堆将原数组当做一个普通的数组),我们将数组 arr[] 从一开始就当做一颗完全二叉树:
然后计算 i = 6/2 - 1 = 2 ,对结点 4(2) 应用堆化操作,发现大于等于其左孩子 4(5) 的值(其中括号中的数字表示下标):
i-- ,i = 1 ,对结点 1(1) 应用堆化操作,计算其左孩子结点 2(3) ,右孩子结点 8(4) ,比较三者大小,发现结点 1(1) 的左右孩子均比其大,将最大结点 8(4) 和 1(1) 交换,此时 1(1) 已经到叶子结点了:
i-- = 0 ,对结点 5(0) 应用堆化操作,发现左孩子 8(3) 比其大,交换两者,继续对 5(3) 进行堆化,发现左右孩子均比其小,堆化结束:
这样我们就得到了一个大顶堆。
for (int i = n / 2 - 1; i >= 0; i--){
heapify(arr, n, i);
}
一个更有意思的问题来了,那你知道刚才讲的 建堆时间复杂度是多少呢?
咋一看,这还不简单,每次调用 Heapify() 函数的时间复杂度为 ,建堆调用了 次,所以刚才讲的建堆操作的时间复杂度就是 量级。
虽然上面的建堆操作的时间复杂度的上限 量级没有错误,但是这个复杂度不是渐近严格的。
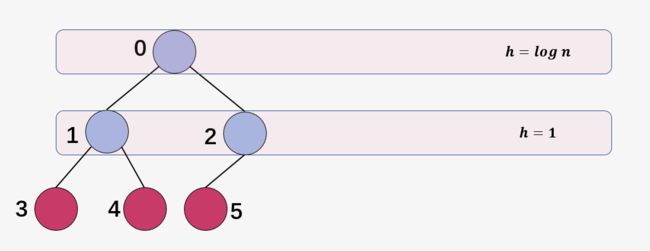
Heapify() 函数的运行时间取决于树的高度 ( , 其中 n 是结点个数),而大多数子树的高度是小于 的。
建堆的循环是从倒数第一层的结点 的位置开始的(其高度为1),一直遍历到根结点 1 位置(高度为 ),因此,堆化(Heapify)对不同的结点的所耗费的时间是不同的,只能暂时认为堆化(Heapify)的运行时间为 ,而这个 是变化的。
要想准确计算出建堆的时间复杂度,就必须知道对于高度为 的顶点的个数是多少。
这里就要告诉大家一个不争的事实啦,对于一个大小为 的堆而言,高度为 的顶点个数最多为 个。比如高度为 1(即 )的结点的个数最多为 个。
那么建堆的时间复杂度就好算了,对于高度为 的结点的运行时间为 ,而 的变化范围为 0 到 ,计算累加和,即:
已知:
那么:
因此,建立一个二叉堆的时间复杂度为 量级。
证明建立一个二叉堆的时间复杂度对于学习堆排序似乎没有特别的意义,但希望考研、学习高等数学的朋友看到数学的魅力,还有数据结构的算法复杂度细究其实还是很有趣的。
推荐阅读:
图解「归并排序」算法(修订版)
图解:什么是快速排序?
漫画:什么是计数排序?
作者:景禹,一个追求极致的共享主义者,想带你一起拥有更美好的生活,化作你的一把伞。