【带权并查集】理论和应用
这篇文章主要讲解带权并查集的理论、设计和实践。
理论
并查集本质
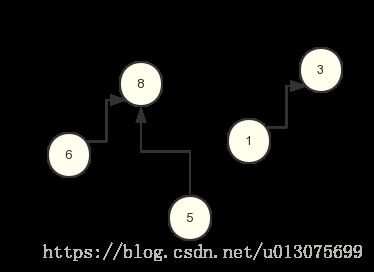
这和以往的并查集模型不太一样。并查集的数据结构使用数组实现时,那么数据结构的本质的是一个含有多棵树的森林。下图是普通并查集的连接情况。
并查集连接方式
每一颗树本身代表其所有结点是在同一集合内,连接整个集合是通过数组的下标代表当前结点的序号,相应数组的值代表其父结点的序号的方式,这样的连接不带有其他关系
带权并查集
而在带权并查集是使得连接集合内的元素之间再添加一层关系,即两个元素之间还带有权值的意义。
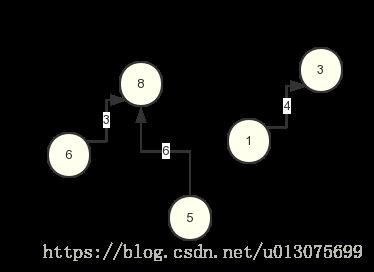
从中我们不难发现普通并查集本质是不带权值的图,而带权并查集则是带权的图。
设计
普通并查集只使用数组id[MAXNUM]表示每个结点的父结点的情况,如果要设计带权并查集,显而易见我们需要另外构造一个数组来表示【权】,假设是R数组。
R数组是代表每个结点与其父结点的权值,也就是每个结点与其父结点的关系。
对于并查集的【并】和【查】操作来说,需要修改的部分:
【并】:并操作的实现有两种,一种是id[qRoot] = pRoot 直接将后面一个结点设置为前一个结点的父结点;另一种是按照树的秩大小决定合并,也叫Quick-Union 算法。
在【先后关系】的情况下,不能按照秩的大小进行合并。后者的算法效率明显优于前者。但是在路径压缩的前提下,后者的优化情况并没有这么明显。
许多文章都是采用前者的方法去做,但是经过不少实践(做题目)过后者的方法也是可以的,因为带权并查集从本质去看没有前后关系,下面会教大家如何在带权并查集下使用。
【查】:采用路径压缩,在将当前结点的父结点指向结点的父结点的父结点,也就是当前结点的父结点指向结点的爷爷结点,id[p] = id[id[p]],在指向之前将当前结点到父结点的权值和父结点到爷爷结点的权值进行处理,这个得具体根据题目决定。
应用
下面以POJ 1182 , HDU 3038这两道例题进行分析带权并查集的具体使用。
POJ 1182
【问题拆分】:假设题目所求的答案为ans。首先x,y不在1到N的范围内,则ans++。如果x,y都在1到N之间,则根据d的值进行相应的合并,合并时保持着关系(权值)。在合并之前进行检查,如果不符合前面的合并则ans++。
这里说到的关系需要利用一个r数组表示该结点与父节点的关系 ,其中r[i]=0代表同一类,r[i]=1代表被父节点吃,r[i]=2代表吃父节点。
刚才我们说过了带权并查集和普通并查集的区别就是在合并和查找(实际上是路径压缩)时对关系进行修改(改变r数组)。
首先我们看路径压缩的情况下,r数组有什么变化
【路径压缩】:路径压缩进行的操作是将当前结点的父结点指向结点的爷爷结点,这个时候r数组会发现什么变化呢,下图是路径压缩的某一个步骤。
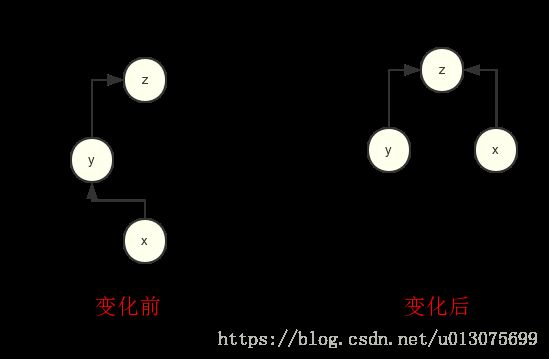
从中可以看出y,z的关系没有改变。其中x指向了z,也就是id[x] = z;x和y的关系不存在,这个可以忽略,因为x和z建立新的关系,会覆盖x和y的关系。也就是r[x]的意义从表示x和y的关系变成x和z的关系。我们通过列出全部的情况进行判断x和z的变化情况。
| (x, y) | (y, z) | (x,z) | 如何判断 |
|---|---|---|---|
| 0 | 0 | 0 | 0+0 = 0 |
| 0 | 1 | 1 | 0+1 = 1 |
| 0 | 2 | 2 | 0+2 = 2 |
| 1 | 0 | 1 | 1+0 = 1 |
| 1 | 1 | 2 | 1+1 = 2 |
| 1 | 2 | 0 | (1+2)% 3 = 0 |
| 2 | 0 | 2 | 2+0 = 2 |
| 2 | 1 | 0 | (2+1)% 3 = 0 |
| 2 | 2 | 1 | (2+2)% 3 = 1 |
我们可以看出经过压缩后x和z的关系,即为r[z] = (r[x] + r[y]) % 3;也就是说在压缩前经历了上面的关系变化。所以路径压缩的代码如下:
// 查找父节点
int Find(int p) {
while (id[p] != id[id[p]]) { //如果q不是其所在子树的根节点的直接孩子
// 更新关系(权值)
r[p] = (r[p] + r[id[p]] ) % 3;
id[p] = id[id[p]]; //对其父节点到其爷爷节点之间的路径进行压缩
}
return id[p];
}【合并】:和路径压缩一样,我们先看看合并后结点的变化。
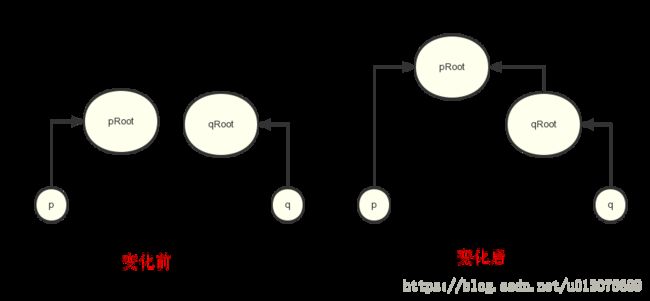
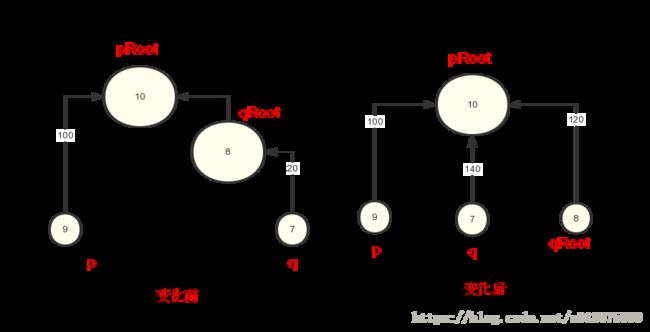
其中可以看出变化的r[qRoot],那么r[qRoot]的变化情况如何求得呢?
这里使用到的是一种【向量思维】去处理,这个非常关键。
结论:qRoot->pRoot = qRoot -> q + q -> p + p ->pRoot
也就是我们求qRoot和pRoot之间的关系时可以通过中间的关系的向量和进行求解。
其中qRoot -> q等于 -r[q], p ->pRoot = r[p],而q -> p需要进行探讨。
现在可以知道r[qRoot] = r[p] - r[q] + q->p;
【由题目可知】,我们在输出p q d时由d可知p和q的关系,如果d = 1时,代表p,q是同类,则q->p = 0。如果d = 2时,代表p吃q,则q->p = 1。所以q->p = d -1 .
所以r[qRoot] = r[p] - r[q] + d - 1,为了保持r数组的值在0-2范围内,
r[qRoot] = (r[p] - r[q] + d - 1 + 3 )% 3。
所以合并的代码如下:
// 合并 p ,q节点
void Union(int p, int q, int d) {
int pRoot = Find(p);
int qRoot = Find(q);
if (pRoot == qRoot) {
return;
}
id[qRoot] = pRoot;
r[qRoot] = (r[p] - r[q] + 3 + (d - 1)) % 3;
}POJ 1182完整代码
#include HDU 3038
由上面题目启发,设置sum数组为当前结点到父结点的和。例如6 10 100,则设置id[6] = 10, sum[6] = 100。代表6的父结点是10,而6到10的和为100。由于A[6] + A[7] + A[8] + A[9] + A[10] = sum[10] - sum[5],所以输入后进行处理,这样在后面的换算中可以直接得出相减得到答案。
同样得,在带权并查集中,使用向量思维去求即可。
【路径压缩】
由于sum数组为当前结点到父结点的和,当将当前结点的父结点指向结点的爷爷结点,r的值需要从【当前结点到父结点的和】变成【当前结点到父结点的和 + 父结点到爷爷结点的和】.代码如下:
// 查找父节点
int Find(int p) {
while (id[p] != id[id[p]]) { //如果q不是其所在子树的根节点的直接孩子
sum[p] = sum[p] + sum[id[p]];
id[p] = id[id[p]]; //对其父节点到其爷爷节点之间的路径进行压缩
}
return id[p];
}【合并】
由于qRoot->pRoot = qRoot -> q + q -> p + p ->pRoot ,
那么sum[qRoot] = - sum[q] + s + sum[p],其中s是p到q的序列和。
例子和演示图
9 10 100
7 8 20
7 9 40
qRoot->pRoot = qRoot -> q + q -> p + p ->pRoot =>
8 -> 10 = 8 -> 7 + 7 ->9 + 9->10 =>
8 -> 10 = -20 + 40 + 100 = 120
所以合并的代码如下:
// 合并 p ,q节点
void Union(int p, int q, int s) {
int pRoot = Find(p);
int qRoot = Find(q);
if (pRoot == qRoot) {
return;
}
id[pRoot] = qRoot;
sum[pRoot] = sum[q] - sum[p] + s;
}完整代码:
#include 练习题
POJ 1962
POJ 1703
POJ 2492
POJ 2912
POJ 1733
HDU 3047
hihoCoder 1515
POJ 1984
题外话:合并操作改写成Quick-Union 算法
(1)从POJ 1182的题目来看,设当前结点序号是p,其父结点是pRoot,则id[p] = pRoot,那么r[p]表示p到pRoot的关系和表示pRoot到p的关系其实都可以。从而可以推导当pRoot和qRoot决定谁做父亲结点时,任一选择其中一个则父亲结点,则相应数组r表示的意思对应上即可。例子假设让pRoot当qRoot的父亲结点,那么id[qRoot] = pRoot,那么qRoot->pRoot = qRoot -> q + q -> p + p ->pRoot =》 r[qRoot] = r[p] - r[q] + d - 1;
反之id[pRoot] = qRoot,pRoot -> qRoot = pRoot -> p + p -> q + q -> qRoot
=>r[pRoot] = r[q] -r[p] + 1 - d。
代码:
// 合并 p ,q节点
void Union(int p, int q, int d) {
int pRoot = Find(p);
int qRoot = Find(q);
if (pRoot == qRoot) {
return;
}
// 按秩进行合并
if (Size[pRoot] > Size[qRoot]) {
id[qRoot] = pRoot;
Size[pRoot] += Size[qRoot];
r[qRoot] = (r[p] - r[q] + 3 + (d - 1)) % 3;
} else {
id[pRoot] = qRoot;
Size[qRoot] += Size[pRoot];
r[pRoot] = (r[q] - r[p] + (1 - d) + 3) % 3;
}
}(2)HDU 3038 ,同理。
// 合并 p ,q节点
void Union(int p, int q, int s) {
int pRoot = Find(p);
int qRoot = Find(q);
if (pRoot == qRoot) {
return;
}
// 按秩进行合并
if (Size[pRoot] > Size[qRoot]) {
id[qRoot] = pRoot;
Size[pRoot] += Size[qRoot];
sum[qRoot] = sum[p] - sum[q] + s;
} else {
id[pRoot] = qRoot;
Size[qRoot] += Size[pRoot];
sum[pRoot] = sum[q] - sum[p] - s;
}
}