Tree(Inorder and Postorder) LEETCODE-100-DAY9
Inorder
应用场景:
- BST适用于升序的序列
230.Kth Smallest Element in a BST(BST & Inorder
Given a binary search tree, write a function kthSmallest to find the kth smallest element in it.
Example 1:
Input: root = [3,1,4,null,2], k = 1
3
/ \
1 4
\
2
Output: 1
Example 2:
Input: root = [5,3,6,2,4,null,null,1], k = 3
5
/ \
3 6
/ \
2 4
/
1
Output: 3
Follow up:
What if the BST is modified (insert/delete operations) often and you need to find the kth smallest frequently? How would you optimize the kthSmallest routine?
Constraints:
- The number of elements of the BST is between
1to10^4. - You may assume
kis always valid,1 ≤ k ≤ BST's total elements.
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
int count;
int res;
public int kthSmallest(TreeNode root, int k) {
count = k;
res = 0;
helper(root);
return res;
}
public void helper(TreeNode root){
if (root == null) return;
helper(root.left);
count--;
if (count == 0) {
res = root.val;
}
helper(root.right);
}
}
Postorder
应用场景:
- 子模块
- 子树
- 从底向上
124.Binary Tree Maximum Path Sum
Given a non-empty binary tree, find the maximum path sum.
For this problem, a path is defined as any sequence of nodes from some starting node to any node in the tree along the parent-child connections. The path must contain at least one node and does not need to go through the root.
Example 1:
Input: [1,2,3]
1
/ \
2 3
Output: 6
Example 2:
Input: [-10,9,20,null,null,15,7]
-10
/ \
9 20
/ \
15 7
Output: 42
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
//找左边最大路径或者右边最大路径和拐点(根节点)的值
class Solution {
int res;//全局变量有值传递和引用传递的区别
public int maxPathSum(TreeNode root) {
if (root == null) return 0;
res = Integer.MIN_VALUE;//求最大值就是 和最小值进行比较
helper(root);
return res;
}
public int helper(TreeNode root) {
if (root == null) return 0;
int left = Math.max(0, helper(root.left));//在这里只取正数
int right = Math.max(0, helper(root.right));
res = Math.max(res, left + right + root.val);
return Math.max(left ,right) + root.val;
}
}
104.Maximum Depth of Binary Tree
Given a binary tree, find its maximum depth.
The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.
Note: A leaf is a node with no children.
Example:
Given binary tree [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
return its depth = 3.
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public int maxDepth(TreeNode root) {
if (root == null) return 0;
int left = maxDepth(root.left) + 1;
return Math.max(left, right);
}
}
[**第九天LeetCode题目(树的Inorder和Postorder)**▼](javascript:void(0)
235. Lowest Common Ancestor of a Binary Search Tree(BST)
Given a binary search tree (BST), find the lowest common ancestor (LCA) of two given nodes in the BST.
According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”
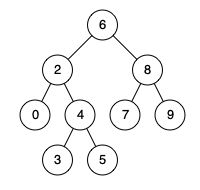
Given binary search tree: root = [6,2,8,0,4,7,9,null,null,3,5]
Example 1:
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
Output: 6
Explanation: The LCA of nodes 2 and 8 is 6.
Example 2:
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
Output: 2
Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.
Note:
- All of the nodes’ values will be unique.
- p and q are different and both values will exist in the BST.
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root.val > p.val && root.val > q.val) {
return lowestCommonAncestor(root.left, p, q);
} else if (root.val < p.val && root.val < q.val) {
return lowestCommonAncestor(root.right, p, q);
} else {
return root;
}
}
}
270. Closest Binary Search Tree Value(BST)付费题
找出BST中离Target值最接近的节点
public int ClosestValue(TreeNode root, double target) {
int res = root.val;
while (root != null) {
//每次和res比较,看哪个更小,看比target大还是小,就知道走左还是右
if (Math.abs(target - root.val) < Math.abs(tartget - res)) {
res = root.val;
}
root = root.val > target ? root.left : root.right;
}
return res;
}
}
173. Binary Search Tree Iterator(BST & Inorder)
Implement an iterator over a binary search tree (BST). Your iterator will be initialized with the root node of a BST.
Calling next() will return the next smallest number in the BST.
Example:
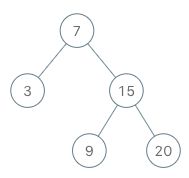
BSTIterator iterator = new BSTIterator(root);
iterator.next(); // return 3
iterator.next(); // return 7
iterator.hasNext(); // return true
iterator.next(); // return 9
iterator.hasNext(); // return true
iterator.next(); // return 15
iterator.hasNext(); // return true
iterator.next(); // return 20
iterator.hasNext(); // return false
Note:
-
next()andhasNext()should run in average O(1) time and uses O(h) memory, where h is the height of the tree. -
You may assume that
next()call will always be valid, that is, there will be at least a next smallest number in the BST whennext()is called.//中序遍历从小到大递增 class BSTIterator { private TreeNode cur; private Stack<TreeNode> stack; public BSTIterator(TreeNode root) { cur = root; stack = new Stack<>(); } /** @return whether we have a next smallest number */ public boolean hasNext() { if (!stack.isEmpty() || cur != null) { return true; } return false; } /** @return the next smallest number */ public int next() { while (cur != null) { stack.push(cur); cur = cur.left; } cur = stack.pop(); int val = cur.val; cur = cur.right; return val; } }
285. Inorder Successor in BST(BST & Inorder)
在BST中找给定节点P的下一个节点是什么
public TreeNode InorderSuccessor(TreeNode root, TreeNode p) {
//判断当前节点和节点P谁的值大
TreeNode res = null;
while (root != null) {
if (root.val <= p.val) {
root = root.right;
} else {
res = root;//root节点可能就是res
root = root.left;
}
return res;
}
99. Recover Binary Search Tree(BST & Inorder)
Share
Two elements of a binary search tree (BST) are swapped by mistake.
Recover the tree without changing its structure.
Example 1:
Input: [1,3,null,null,2]
1
/
3
\
2
Output: [3,1,null,null,2]
3
/
1
\
2
Example 2:
Input: [3,1,4,null,null,2]
3
/ \
1 4
/
2
Output: [2,1,4,null,null,3]
2
/ \
1 4
/
3
Follow up:
- A solution using O(n) space is pretty straight forward.
- Could you devise a constant space solution?
class Solution {
TreeNode first = null;
TreeNode second = null;
TreeNode prev = null;//记录前一个节点,总比前一个节点大(二叉树性质)
public void recoverTree(TreeNode root) {
if (root == null) return;
helper(root);
int temp = first.val;
first.val = second.val;
second.val = temp;
}
public void helper(TreeNode root) {
if (root == null) return;
helper(root.left);//从左边的叶节点开始执行,
if (prev != null && prev.val >= root.val) {
if (first == null) first = prev;
second = root;
}
prev = root;
helper(root.right);
}
}
124. Binary Tree Maximum Path Sum(Postorder)
Given a non-empty binary tree, find the maximum path sum.
For this problem, a path is defined as any sequence of nodes from some starting node to any node in the tree along the parent-child connections. The path must contain at least one node and does not need to go through the root.
Example 1:
Input: [1,2,3]
1
/ \
2 3
Output: 6
Example 2:
Input: [-10,9,20,null,null,15,7]
-10
/ \
9 20
/ \
15 7
Output: 42
//找左边最大路径或者右边最大路径和拐点(根节点)的值
class Solution {
int res;//全局变量有值传递和引用传递的区别
public int maxPathSum(TreeNode root) {
if (root == null) return 0;
res = Integer.MIN_VALUE;//求最大值就是 和最小值进行比较
helper(root);
return res;
}
public int helper(TreeNode root) {
if (root == null) return 0;
int left = Math.max(0, helper(root.left));//在这里只取正数
int right = Math.max(0, helper(root.right));
res = Math.max(res, left + right + root.val);
return Math.max(left ,right) + root.val;
}
}
250. Count Univalue Subtrees(Postorder)付费题
有多少个Subtree有同样的val
HINT:单独的叶子节点也算一个子树
//PostOrder
//time:O(n)遍历一遍
//space:O(n)
int res;
public int countUnivalueSubtrees(TreeNode root) {
res = 0;
helper(res);
return res;
}
public boolean helper(TreeNode root) {
if (root == null) return true;
boolean left = helper(root.left);//子树为空的时候为TRUE
boolean right = helper(root.right);
if (left && right) {
if (root.left != null && root.val != root.left.val) {
return false;
}
if (root.right != null && root.val != root.right.val) {
return false;
}
res++;
return true;
}
return false;
}
236.Lowest Common Ancestor of a Binary Tree(Postorder)
Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.
According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”
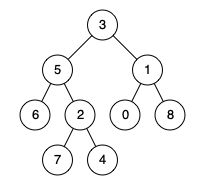
Given the following binary tree: root = [3,5,1,6,2,0,8,null,null,7,4]
Example 1:
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
Output: 3
Explanation: The LCA of nodes 5 and 1 is 3.
Example 2:
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
Output: 5
Explanation: The LCA of nodes 5 and 4 is 5, since a node can be a descendant of itself according to the LCA definition.
Note:
- All of the nodes’ values will be unique.
- p and q are different and both values will exist in the binary tree.
//Preorder是从上到下,Postorder是从下到上
//typical, needs to be memorized
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root == null || root == p || root == q) return root;
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
if (left != null && right != null) {
return root;
}
return left == null ? right : left;//叶子节点,或者单子树节点
}
}
366. Find Leaves of Binary Tree(Postorder)付费题
找出BST中所有的叶子节点
[4, 5, 3] [2] [1]
public List<List<Integer>> findLeaves (TreeNode root) {
//有顺序,就要有一个level
List<List<Integer>> res = new ArrayList<>();
helper(res, root);
return res;
}
private int helper(List<List<Integer>> res, TreeNode root) {
if (root == null) return -1;
int left = helper(res, root.left);
int right = helper(res, root.right);
int level = Math.max(left, right) + 1;//叶子节点是第0层,因为叶子节点也有左右子树,都为0,为NULL层
if (res.size() == level) {
res.add(new ArrayList<>());
}
res.get(level).add(root.val);//将值加入对应层
root.left = null;
root.right = null;
return level;
}