离散数学-2 命题逻辑等值演算
求公式主析取范式的方法步骤:
方法一:等值演算
设公式A含命题变项p1,p2,…,pn
(1) 求A的析取范式A=B1B2 … Bs , 其中Bj是简单合取
式 j=1,2, … ,s
(2) 若某个Bj既不含pi, 又不含Øpi, 则将Bj展开成
Bj Bj(pipi) (Bjpi)(Bjpi)
重复这个过程, 直到所有简单合取式都是长度为n的极
小项为止
(3) 消去重复出现的极小项, 即用mi代替mimi
(4) 将极小项按下标从小到大排列
方法二:真值表
(1) 写出A的真值表
(2)求出A的成真赋值
(3) 写出成真赋值对应的极小项,按角标从小到大析取
求公式的主合取范式的步骤:
方法一:等值演算
设公式A含命题变项p1,p2,…,pn
(1) 求A的合取范式A=B1B2 … Bs , 其中Bj是简单析取
式 j=1,2, … ,s
(2) 若某个Bj既不含pi, 又不含Øpi, 则将Bj展开成
Bj Bj(pipi) (Bjpi)(Bjpi)
重复这个过程, 直到所有简单析取式都是长度为n的极
大项为止
(3) 消去重复出现的极大项, 即用Mi代替MiMi
(4) 将极大项按下标从小到大排列
方法二:真值表
(1) 写出A的真值表
(2)求出A的成假赋值
(3) 写出成假赋值对应的极大项,按角标从小到大合取
方法三:由主析取范式求主合取范式
主范式的应用
1.求公式的成真成假赋值
设公式A含n个命题变项, A的主析取范式有s个极小项, 则A
有s个成真赋值, 它们是极小项下标的二进制表示, 其余2n-s
个赋值都是成假赋值
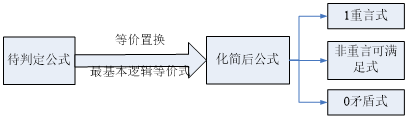
2. 判断公式的类型
设A含n个命题变项.
A为重言式 A的主析取范式含全部2n个极小项
A的主合取范式不含任何极大项, 记为1.
A为矛盾式 A的主合析取范式含全部2n个极大项
A的主析取范式不含任何极小项, 记为0.
A为非重言式的可满足式
A的主析取范式中至少含一个、但不是全
部极小项
A的主合取范式中至少含一个、但不是全
部极大项.
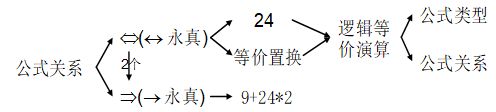
3. 判断两个公式是否等值
4. 解实际问题
定义2.1 若等价式AB是重言式,则称A与B等值,记作AB,并称AB是等值式
16组等值式模式
双重否定律 AA
幂等律 AAA, AAA
交换律 ABBA, ABBA
结合律 (AB)CA(BC), (AB)CA(BC)
分配律 A(BC)(AB)(AC), A(BC)(AB)(AC)
德摩根律 (AB)AB, (AB)AB
吸收律 A(AB)A, A(AB)A
零律 A11, A00
同一律 A0A. A1A
排中律 AA1
矛盾律 AA0
蕴涵等值式 ABAB
等价等值式 AB(AB)(BA)
假言易位 ABBA
等价否定等值式 ABAB
归谬论 (AB)(AB) A
等值演算:由已知等值式推演出新的等值式的过程
置换规则:若A,则Φ(A)Φ(B)
定义2.2、2.3
(1) 文字——命题变项及其否定的总称(说明:单个文字既是简单析取式又是简单合取式)
(2) 简单析取式——有限个文字构成的析取式: p, q, pq, pqr, …
(3) 简单合取式——有限个文字构成的合取式:p, q, pq, pqr, …
(4) 析取范式——由有限个简单合取式组成的析取式
p, pq, pq, (pq)(pqr)(qr)
(5) 合取范式——由有限个简单析取式组成的合取式
p, pq, pq, (pqp(pqr)
(6) 范式——析取范式与合取范式的总称
定理2.1 (1) 一个简单析取式是重言式当且仅当它同时含有某个命题变项和它的否定式.
(2) 一个简单合取式是矛盾式当且仅当它同时含有某个命题变项和它的否定式.
定理2.2 (1) 一个析取范式是矛盾式当且仅当它每个简单合取式都是矛盾式.
(2) 一个合取范式是重言式当且仅当它的每个简单析取式都是重言式.
定理2.3(范式存在定理)
任何命题公式都存在与之等值的析取范式与合取范式
定义2.4 在含有n个命题变项的简单合取式(简单析取式)中,若每个命题变项均以文字的形式在其中出现且仅出现一次,而且第i个文字出现在左起第i位上(1in),称这
样的简单合取式(简单析取式)为极小项(极大项).
定义2.5
主析取范式——由极小项构成的析取范式
主合取范式——由极大项构成的合取范式
定理2.5 (主范式的存在惟一定理)
任何命题公式都存在与之等值的主析取范式和主合取范式,并且是惟一的。
定义2.6称F:{0,1}n {0,1} 为n元真值函数.F的自变量是n个命题变项,定义域为:
![]()
任何一个含n个命题变项的命题公式A,都唯一地存在一个n元真值函数与之等值。
定义2.7设S是一个联结词集合,如果任何n(n1) 元真值函数都可以由仅含S中的联结词构成的公式表示,则称S是联结词完备集
定理2.6S = {, , }是联结词完备集
推论 以下都是联结词完备集
(1) S1 = {, , , } (2) S2 = {, , , , }
(3) S3 = {, } (4) S4 = {, }
(5) S5 = {, }
定义2.8设p, q 为两个命题, (pq)称作p与q的与非式, 记作pq, 即 pq (pq), 称为与非联结词;(pq) 称作 p 与 q 的或非式, 记作 pq, 即 pq (pq), 称为或非联结词
定理2.7 {}与{}为联结词完备集.
不含任何文字的简单析取式称作空简单析取式,记作. 规定是不可满足的.
约定:简单析取式不同时含某个命题变项和它的否定
S:合取范式,C:简单析取式,l:文字,:赋值,文字l的补lc:若l=p,则lc=p;若l=p,则lc=p.用SS表示S是可满足的当且仅当S是可满足的
定义2.9 设C1=lC1, C2=lcC2, C1和C2不含l和lc, 称C1C2为C1和C2(以l和lc为消解文字)的消解式或消解结果, 记作Res(C1,C2)
例如, Res(pqr, pqs)= qrs
定理2.8C1C2Res(C1,C2)
注意: C1C2与Res(C1,C2)有相同的可满足性, 但不一定等值.
定义2.10 设S是一个合取范式, C1,C2,,Cn是一个简单析取式序列. 如果对每一个i(1in), Ci是S的一个简单析取式或者是Res(Cj,Ck)(1j<k<i), 则称此序列是由S导出Cn的消解序列. 当Cn=时, 称此序列是S的一个否证.
定理2.9一个合取范式是不可满足的当且仅当它有否证.
例用消解规则证明S=(pq)(pqs)(qs)q是不可满足的.
证 C1=pq, C2= pqs, C3=Res(C1,C2)=qs, C4=qs,
C5=Res(C3,C4)=q, C6=q, C7=Res(C5,C6)=, 这是S的否证.
消解算法(知道怎么用就行)
输入: 合式公式A
输出: 当A是可满足时, 回答"Yes"; 否则回答"No".
1. 求A的合取范式S
2. 令S0, S2, S1S的所有简单析取式
3. For C1S0和C2S1
4. If C1, C2可以消解 then
5. 计算CRes(C1,C2)
6. If C= then
7. 输出"No", 计算结束 (中间算出个否证那就不可满足了)
8. If CS0且CS1 then
9. S2S2{C}
10. For C1S1, C2S1且C1C2
11. If C1, C2可以消解 then
12. 计算CRes(C1,C2)
13. If C= then
14. 输出"No", 计算结束 (中间算出个否证那就不可满足了)
15. If CS0且CS1 then
16. S2S2{C}
17. If S2= then
18. 输出"Yes", 计算结束
19. Else S0S0S1, S1S2, S2, goto 3
例用消解算法判断下述公式是否是可满足的:
p(pq)(pq)(qr)(qr)
解 S= p(pq)(pq)(qr)(qr)
循环1 S0=, S1={p, pq, pq, qr, qr}, S2= |
2,构造出三个集合,S自身产生的放在S1 |
Res(pq, pq)=p |
10,S1中两两可消解的互消 |
Res(pq, qr)=pr |
10,S1中两两可消解的互消 |
Res(pq, qr)= pr |
10,S1中两两可消解的互消 |
Res(qr, qr)=q |
10,S1中两两可消解的互消 |
S2={pr, pr, q} |
16 更新S2的值 |
循环2 S0={p, pq, pq, qr, qr}, S1={pr, pr, q}, S2= |
19 S0变成与S1的并集这里即原来的简单析取式集合,S1变成了S2即上个循环的消解结果,S2变成了空集 |
Res(pq, q)=p |
3 S0与S1中可消解的进行消解 |
Res(qr, pr)=pq |
3 S0与S1中可消解的进行消解 |
Res(qr, pr)=pq |
3 S0与S1中可消解的进行消解 |
Res(pr, pr)=p |
3 S0与S1中可消解的进行消解 |
S2= |
17 最后发现消解的结果已经有了,S2为空集所以yes |
输出"Yes" |
计算结束 |
题型
1、用等值演算法证明重言式和矛盾式
重言式:一般是演算到A1;特别地,要证A↔B是重言式即证AB是比证明证A↔B1要更容易。
矛盾式:演算到A0
2、用等值演算法证明等值式
从左往右或是从右往左运用16组等值式模式证明即可
3、通过求公式的主析取范式或主合取范式判断公式的类型
设A是含n个命题变项的公式,A的类型与它的主析取范式和主合取范式有如下的关系:
4、用主析取范式判断两个公式是否等值
AB当且仅当A与B有相同的主析取范式
5、将已知的命题公式等值地化成给定联结词完备集
答案不唯一但等值,可用真值表检查。
6、用等值演算法求解实际问题
某公司要从赵、钱、孙、李、周五名新毕业的大学生中选
派一些人出国学习. 选派必须满足以下条件:
(1) 若赵去,钱也去.
(2) 李、周两人中至少有一人去
(3) 钱、孙两人中去且仅去一人.
(4) 孙、李两人同去或同不去.
(5) 若周去,则赵、钱也去.
用等值演算法分析该公司如何选派他们出国?
解此类问题的一般步骤:
1.设简单命题并符号化
2. 用复合命题描述各条件
3. 写出由复合命题组成的合取式
4. 将合取式成析取式(最好是主析取范式)
5. 求成真赋值, 并做出解释和结论
解
1. 设简单命题并符号化
设 p: 派赵去,q: 派钱去,r: 派孙去,s: 派李去,u: 派周去
2. 写出复合命题
(1) 若赵去,钱也去 pq
(2) 李、周两人中至少有一人去 su
(3) 钱、孙两人中去且仅去一人 (qr)(qr)
(4) 孙、李两人同去或同不去 (rs)(rs)
(5) 若周去,则赵、钱也去 u(pq)
3.设(1)—(5)构成的合取式为A
A = (pq)(su)((qr)(qr))
((rs)(rs))(u(pq))
4. 化成析取式
A (pqrsu)(pqrsu)
结论:由上述析取式可知,A的成真赋值为00110与11001,
派孙、李去(赵、钱、周不去)
派赵、钱、周去(孙、李不去)
7、消解规则及其性质、消解序列、消解算法解决可满足性问题
一个合取范式是不可满足的当且仅当它有否证.
设S是一个合取范式, C1,C2,,Cn是一个简单析取式序列. 如果对每一个i(1in), Ci是S的一个简单析取式或者是Res(Cj,Ck)(1j<k<i), 则称此序列是由S导出Cn的消解序列. 当Cn=时, 称此序列是S的一个否证.