数据结构与算法-排序篇-Python描述
前言
补习基础的数据结构和算法的时候,很多都是用c或者java写的,顺便我用python重构一遍吧,也当做是补习了~
排序算法
冒泡排序
冒泡排序原理即:从数组下标为0的位置开始,比较下标位置为0和1的数据,如果0号位置的大,则交换位置,如果1号位置大,则什么也不做,然后右移一个位置,比较1号和2号的数据,和刚才的一样,如果1号的大,则交换位置,以此类推直至最后一个位置结束,到此数组中最大的元素就被排到了最后,之后再根据之前的步骤开始排前面的数据,直至全部数据都排序完成。
就是传说中的大的沉到底原则,适用于小量数据
def bubbleSort(relist):
len_ = len(relist)
for i in range(len_):
print("第 %s 趟排序"%(i+1))
for j in range(0,len_-i-1):
if relist[j] > relist[j+1]:
relist[j+1], relist[j] = relist[j], relist[j+1]
return relist
print (bubbleSort([1,5,2,6,6,9,3]))
print (bubbleSort([1, 2, 3, 5, 6, 6, 9]))
第 1 趟排序
第 2 趟排序
第 3 趟排序
第 4 趟排序
第 5 趟排序
第 6 趟排序
第 7 趟排序
[1, 2, 3, 5, 6, 6, 9]
第 1 趟排序
第 2 趟排序
第 3 趟排序
第 4 趟排序
第 5 趟排序
第 6 趟排序
第 7 趟排序
[1, 2, 3, 5, 6, 6, 9]
优化一下冒泡,如果发现没有一次交换,则已经有序,不再进行遍历
# 优化后的冒泡
def bubbleSort(relist):
len_ = len(relist)
for i in range(len_):
flag = False
print("第 %s 趟排序"%(i+1))
for j in range(0,len_-i-1):
if relist[j] > relist[j+1]:
relist[j+1], relist[j] = relist[j], relist[j+1]
flag = True
if flag is False:
return relist
return relist
print (bubbleSort([1,5,2,6,6,9,3]))
print (bubbleSort([1, 2, 3, 5, 6, 6, 9]))
第 1 趟排序
第 2 趟排序
第 3 趟排序
第 4 趟排序
第 5 趟排序
[1, 2, 3, 5, 6, 6, 9]
第 1 趟排序
[1, 2, 3, 5, 6, 6, 9]
最后盗一张神图,最大的一直是沉到底的
选择排序
基本思想(参考自–选择排序):第1趟,在待排序记录r1 ~ r[n]中选出最小的记录,将它与r1交换;第2趟,在待排序记录r2 ~ r[n]中选出最小的记录,将它与r2交换;以此类推,第i趟在待排序记录r[i] ~ r[n]中选出最小的记录,将它与r[i]交换,使有序序列不断增长直到全部排序完毕。
[外链图片转存失败(img-pBh1LNdU-1566451174122)(https://img-my.csdn.net/uploads/201208/28/1346124560_3555.jpg)]
# 方法一
def selectSort(relist):
len_ = len(relist)
for i in range(len_):
min_index = i
for j in range(i+1,len_): # 这个循环会找到值比第i个索引所代表值小的索引
if relist[j] < relist[min_index]:
min_index = j
relist[i] ,relist[min_index] = relist[min_index], relist[i] # 互换两个索引位置
return relist
print selectSort([1,5,2,6,9,3])
# 方法二,更加简便,但是注意和冒泡法进行区分
def selectSort(relist):
for i in range(len(relist)):
for j in range(len(relist)-i):
if relist[i] > relist[i+j]:
relist[i],relist[i+j] = relist[i+j],relist[i]
return relist
print selectSort([1,5,2,6,9,3])
快速排序
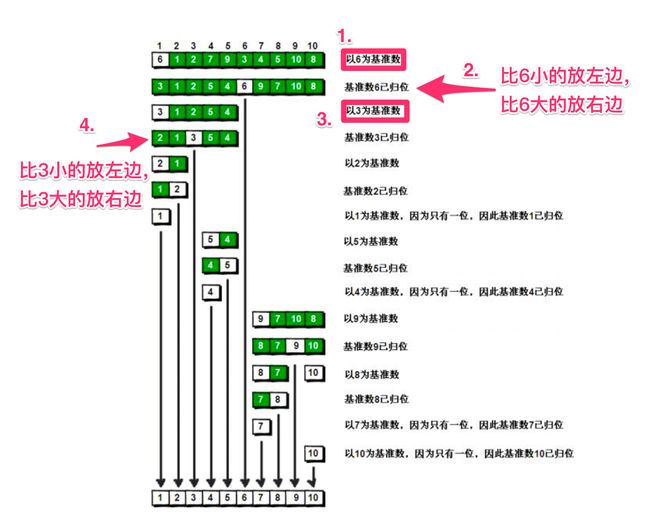
该方法的基本思想是(参考自–白话经典算法系列之六 快速排序 快速搞定):
- 先从数列中取出一个数作为基准数。
- 分区过程,将比这个数大的数全放到它的右边,小于或等于它的数全放到它的左边。
- 再对左右区间重复第二步,直到各区间只有一个数。
# 快排 分片的思想+递归的思想,这是取了第一个为基准值,栈高为O(log(n)),栈长O(n),所以运行时间为栈高x栈长,也就是算法平均运算时间为O(nlog(n))
def quickSort(array):
if len(array) < 2:
return array
else:
pivot = array[0]
less = [i for i in array[1:] if i < pivot]
greater = [j for j in array[1:] if j >= pivot]
return quickSort(less) + [pivot] + quickSort(greater)
print quickSort([1,5,5,2,6,9,3])
插入排序
插入排序就是每一步都将一个待排数据按其大小插入到已经排序的数据中的适当位置,直到全部插入完毕。
- 默认序列中的第0个元素是有序的(因为只有一个元素a[0]嘛,自然是有序的);
- 从下标为1(下标0没啥好插的)的元素开始,取当前下标i位置处的元素a[i]保存到一个临时变量waitInsert里;
- waitInsert与对前半部分有序序列的循环遍历比较,直到遇到第一个比waitInsert大的元素(这里默认是从小到大排序),此时的下标为j,然后将其插入到j的位置即可;
- 因为前面的插入,导致后面元素向后推移一个位置,没关系,把原来下标i的元素弹出即可;
- 重复进行第2步到第4步,直到乱序序列中的元素被全部插入到有序序列中;
- 经过以上5个步骤之后,整体序列必然有序,排序完成。
# 直接插入排序
def insertSort(relist):
len_ = len(relist)
for i in range(1,len_):
for j in range(i):
if relist[i] < relist[j]:
relist.insert(j,relist[i]) # 首先碰到第一个比自己大的数字,赶紧刹车,停在那,所以选择insert
relist.pop(i+1) # 因为前面的insert操作,所以后面位数+1,这个位置的数已经insert到前面去了,所以pop弹出
break
return relist
print insertSort([1,5,2,6,9,3])
希尔排序
希尔(Shell)排序又称为缩小增量排序,它是一种插入排序。它是直接插入排序算法的一种威力加强版。–From排序四 希尔排序
- 在第一趟排序中,我们不妨设 gap1 = N / 2 = 5,即相隔距离为 5 的元素组成一组,可以分为 5 组。
接下来,按照直接插入排序的方法对每个组进行排序。
- 在第二趟排序中,我们把上次的 gap 缩小一半,即 gap2 = gap1 / 2 = 2 (取整数)。这样每相隔距离为 2 的元素组成一组,可以分为 2 组。
按照直接插入排序的方法对每个组进行排序。
-
在第三趟排序中,再次把 gap 缩小一半,即gap3 = gap2 / 2 = 1。 这样相隔距离为 1 的元素组成一组,即只有一组。
按照直接插入排序的方法对每个组进行排序。此时,排序已经结束。
需要注意一下的是,图中有两个相等数值的元素 5 和 5 。我们可以清楚的看到,在排序过程中,两个元素位置交换了。
所以,希尔排序是不稳定的算法。
![]()
def shell_sort(relist):
n = len(relist)
gap = n/2 # 初始步长
while gap > 0:
for i in range(gap, n):
temp = relist[i] # 每个步长进行插入排序
j = i
# 插入排序
while j >= gap and relist[j - gap] > temp:
relist[j] = relist[j - gap]
j -= gap
relist[j] = temp
gap = gap/2 # 得到新的步长
return relist
print shell_sort([1,5,2,6,9,3])
归并排序
参考自–归并排序算法原理分析与代码实现:假设我们有一个没有排好序的序列(14,12,15,13,11,16),那么首先我们使用分割的办法将这个序列分割成一个个已经排好序的子序列。然后再利用归并的方法将一个个的子序列合并成排序好的序列。分割和归并的过程可以看下面的图例。这样通过先递归的分解数列,再合并数列就完成了归并排序。
def merge(left,right):
result = []
while left and right:
result.append(left.pop(0) if left[0] <= right[0] else right.pop(0))
while left:
result.append(left.pop(0))
while right:
result.append(right.pop(0))
return result
def mergeSort(relist):
if len(relist) <= 1:
return relist
mid_index = len(relist)/2
left = mergeSort(relist[:mid_index]) # 递归拆解的过程
right = mergeSort(relist[mid_index:])
return merge(left,right) # 合并的过程
print mergeSort([1,5,2,6,9,3])
# 关于pop的用法
a = [1,2,3,4]
print a.pop(0)
print a
# 1
# [2, 3, 4]
堆排序
原理:深度好文请先看这里,然后在看接下来的,切记,还有这个!- 利用Python实现堆排序
- 创建最大堆:将堆所有数据重新排序,使其成为最大堆
- 最大堆调整:作用是保持最大堆的性质,是创建最大堆的核心子程序
- 堆排序:移除位在第一个数据的根节点,并做最大堆调整的递归运算
# code from -http://blog.csdn.net/minxihou/article/details/51850001
import random
def MAX_Heapify(heap,HeapSize,root):#在堆中做结构调整使得父节点的值大于子节点
left = 2*root + 1
right = left + 1
larger = root
if left < HeapSize and heap[larger] < heap[left]:
larger = left
if right < HeapSize and heap[larger] < heap[right]:
larger = right
if larger != root:#如果做了堆调整则larger的值等于左节点或者右节点的,这个时候做对调值操作
heap[larger],heap[root] = heap[root],heap[larger]
MAX_Heapify(heap, HeapSize, larger)
def Build_MAX_Heap(heap):#构造一个堆,将堆中所有数据重新排序
HeapSize = len(heap)#将堆的长度当独拿出来方便
for i in xrange((HeapSize -2)//2,-1,-1):#从后往前出数
MAX_Heapify(heap,HeapSize,i)
def HeapSort(heap):#将根节点取出与最后一位做对调,对前面len-1个节点继续进行对调整过程。
Build_MAX_Heap(heap)
for i in range(len(heap)-1,-1,-1):
heap[0],heap[i] = heap[i],heap[0]
MAX_Heapify(heap, i, 0)
return heap
if __name__ == '__main__':
a = [30,50,57,77,62,78,94,80,84]
print a
HeapSort(a)
print a
b = [random.randint(1,1000) for i in range(1000)]
#print b
HeapSort(b)
print b
复杂度比较
| 排序法 | 最差时间分析 | 平均时间复杂度 | 稳定度 | 空间复杂度 |
|---|---|---|---|---|
| 冒泡排序 | O(n^2) | O(n^2) | 稳定 | O(1) |
| 快速排序 | O(n^2) | O(n*log2n) | 不稳定 | O(log2n)~O(n) |
| 选择排序 | O(n^2) | O(n^2) | 不稳定 | O(1) |
| 二叉树排序 | O(n^2) | O(n*log2n) | 不一顶 | O(n) |
| 插入排序 | O(n^2) | O(n^2) | 稳定 | O(1) |
| 堆排序 | O(n*log2n) | O(n*log2n) | 不稳定 | O(1) |
| 希尔排序 | O | O | 不稳定 | O(1) |
更新
- 2017.9.4 - 更新- 常见排序算法
致谢
- 基础排序总结(冒泡排序、选择排序、插入排序)
- 图解排序算法(一)之3种简单排序(选择,冒泡,直接插入)
- 排序四 希尔排序