【python算法】图的遍历与最小路径

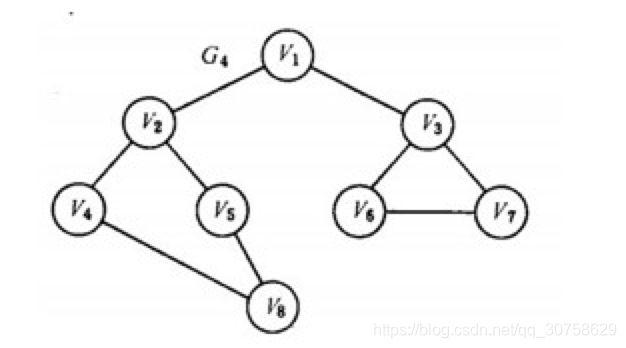
数据结构中，图的应用场景非常广泛，与我们的生活息息相关，在基于图做的应用中，比较典型的有：在交通规划中的最小生成树，用于导航的最短路径等。比如下图

 

这里，我们介绍邻接表表示方法。

在表示图的时，我们一般使用如下的两个实例属性，表示邻接表的字典nodeNeighbors，标志是否已访问的字典visited。

针对如下的图：来实现广度优先遍历以及深度优先遍历还用求最短路径：

 

简述思想：

1.定义一个图的类class Graph，定义nodeNeighbors和visited；nodeNeighbors表示：存储每一个节点可以到达的所有节点和权重，visited记录节点是否被访问过

2.增加 添加节点,添加有权边，返回所有node的方法

添加节点：就是nodeNeighbors[node] = []

添加有权边：nodeNeighbors[u].append((v, var))

返回节点很简单：直接返回key return self.nodeNeighbors.keys()

# 定义图类
class Graph(object):
    def __init__(self):
        self.nodeNeighbors = {}  # 存储一个节点可到达的所有节点，
        # 比如上图就是self.nodeNeighbors = {1: [(2, 1), (3, 1), (5, 1)], 2: [], 3: [(4, 1)], 4: [], 5: []} key为node，元组[0]代表到达的节点，元组[1]代表权重，就是路径的大小，此处默认为1
        self.visited = {}  # 存储所有被访问的节点，value为True表示被访问过了 例如 {1: True, 2: True, 3: True, 5: True, 4: True}

    # 添加节点
    def addNode(self, node):
        if node not in self.nodeNeighbors:
            self.nodeNeighbors[node] = []

    # 批量添加节点
    def addNodes(self, nodeList):
        for node in nodeList:
            self.addNode(node)

    # 添加有权边 例如addEdge((1, 2)，1代表开始的node，2代表结束的node，var是权重，目前都默认为1
    def addEdge(self, edge, var=1):
        u, v = edge
        if u == v: #如果起点和终点一样，就直接return
            return None
        if v not in [x[0] for x in self.nodeNeighbors[u]]:  #self.nodeNeighbors[1]]就是[(2, 1), (3, 1), (5, 1)]，x[0]就是每个可到达的node
            self.nodeNeighbors[u].append((v, var))
            return 1
        else:
            return 0

    # 返回所有节点
    def nodes(self):
        return self.nodeNeighbors.keys()

3.简述广度优先遍历方法的思想

定义queue一个队列，存储待遍历的node，先进先出

定义order，存储遍历后的结果的，最后return的是order

定义bfs函数，如果queue不为空，while循环，取出第一个node,标记为visit后，遍历nodeNeighbors[node],如果没被visit也没有夹到过queue，就增加

    def breathFirthSearch(self, root=None):
        queue = []  # 存储待遍历的节点对象，利用先进先出的方式进行广度遍历
        order = []  # 存储遍历后的节点值

        def bfs():  # 遍历函数
            while len(queue) > 0:
                node = queue.pop(0)
                self.visited[node] = True  # 设定队列出去的节点被遍历过
                for n, v in self.nodeNeighbors[node]: #nodeNeighbors[1]]就是[(2, 1), (3, 1), (5, 1)]
                    # 如果当前节点不在被访问的节点中，也不再待遍历的队列中
                    # 则将此节点添加到带遍历队列，并且把元素值添加到order队列
                    # 使用2个条件的原因，在于节点虽然没有被访问，但是已经在queue里面了
                    if (n not in self.visited) and (n not in queue):
                        queue.append(n)
                        order.append(n)
        if root:
            queue.append(root)
            order.append(root)
            bfs()

        # 如果有些节点是一些单独的节点
        # 不和任何其他节点相连，就要用此循环来保证遍历到
        for node in self.nodes():
            if node not in self.visited:
                queue.append(node)
                order.append(node)
                bfs()
        return order

4.简述深度优先遍历的思想：

运用递归，如果node没被visit，order先append(node),循环nodeNeighbors[node]，如果里面的node没被visit，递归dfs(n)

    def depthFirstSearch(self, root=None):
        order = []
        def dfs(node):
            if node not in self.visited:
                order.append(node)
                self.visited[node] = True
                for n, v in self.nodeNeighbors[node]:  # ##{1:[(2:1),(3:1),(5:1)]}
                    # 使用递归进行深度遍历
                    if n not in self.visited:
                        dfs(n)

        # 从根节点进行遍历
        if root:
            dfs(root)

        # 如果有些节点是一些单独的节点
        # 不和任何其他节点相连，就要用此循环来保证遍历到
        for node in self.nodes():
            if node not in self.visited:
                dfs(node)

        return order

5.简述最短路径思路：

1.从source节点，进行广度遍历（先把source放到队列中，遍历）

while len(q) > 0:

q.append((alt,n))

2.遍历每一个节点，把source到这个节点的距离算出来 alt = distance+v

3.如果这个alt在dist字典（到source的最短距离）中没存过，就存 dist[n] = alt

4.如果alt在dist字典存过了，比较alt和dist[n]哪个更小，如果alt更小，则更新dist[n]=alt,且把n和当前到最小距离从新放在队列里

队列中基于最短距离重新做广度遍历

    def shorestPath(self, source):
        dist = {source:0}
        q = [(0,source)]
        while len(q) > 0:
            distance, node = q.pop(0)
            self.visited[node] = True
            for n,v in self.nodeNeighbors[node]:
                alt = distance + v
                if n not in self.visited:
                    if (n not in dist) or alt < dist[n]:
                        dist[n] = alt
                        q.append((alt,n))
                if n in self.visited and n in dist and alt < dist[n]:
                    dist[n] = alt
                    q.append((alt,n))
        return dist