poj 1456 Supermarket (贪心， 并查集)

链接：

http://poj.org/problem?id=1456

题目：

Description

A supermarket has a set Prod of products on sale. It earns a profit px for each product x∈Prod sold by a deadline dx that is measured as an integral number of time units starting from the moment the sale begins. Each product takes precisely one unit of time for being sold. A selling schedule is an ordered subset of products Sell ≤ Prod such that the selling of each product x∈Sell, according to the ordering of Sell, completes before the deadline dx or just when dx expires. The profit of the selling schedule is Profit(Sell)=Σ _x∈Sellpx. An optimal selling schedule is a schedule with a maximum profit. 
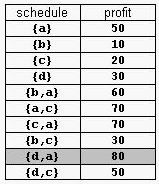
For example, consider the products Prod={a,b,c,d} with (pa,da)=(50,2), (pb,db)=(10,1), (pc,dc)=(20,2), and (pd,dd)=(30,1). The possible selling schedules are listed in table 1. For instance, the schedule Sell={d,a} shows that the selling of product d starts at time 0 and ends at time 1, while the selling of product a starts at time 1 and ends at time 2. Each of these products is sold by its deadline. Sell is the optimal schedule and its profit is 80. 

Write a program that reads sets of products from an input text file and computes the profit of an optimal selling schedule for each set of products. 

Input

A set of products starts with an integer 0 <= n <= 10000, which is the number of products in the set, and continues with n pairs pi di of integers, 1 <= pi <= 10000 and 1 <= di <= 10000, that designate the profit and the selling deadline of the i-th product. White spaces can occur freely in input. Input data terminate with an end of file and are guaranteed correct.

Output

For each set of products, the program prints on the standard output the profit of an optimal selling schedule for the set. Each result is printed from the beginning of a separate line.

Sample Input

4  50 2  10 1   20 2   30 1

7  20 1   2 1   10 3  100 2   8 2
   5 20  50 10

Sample Output

80
185

题目大意：

超市里有n个产品要卖，每个产品都有一个截至时间dx（从开始卖时算起），只有在这个截至时间之前才能卖出并且获得率润dy。

有多个产品，所有可以有不同的卖出顺序，每卖一个产品要占用1个单位的时间，问最多能卖出多少利润。

思路与总结：

这是并查集专题中的一道题， 但是我怎么看都长得像是贪心题，于是顺着贪心的思路AC了.

因为每卖一个产品要占用一个时间单位，所以，我们可以一个单位一个单位时间地依次决定，每个时间要卖哪个产品，并且保证每个单位时间卖出的产品都是利润最大的，这样便能保证最终结果是最大的。

如果枚举时间从小到大的话，那么比较麻烦，更好的办法是从最后一个截至时间开始往前枚举， 这样的话，只要把截止时间大于这个时间段的产品都放入优先队列，其中利润最大的便是这时间所要的。 这个方法用排序+优先队列实现， 复杂度是 n log n， 在poj上用了 63ms

但毕竟是并查集专题，于是又想了并查集的方法做。想了很久，发现实在是很难想到。于是偷偷地看了下用了并查集的题解，发现无法理解。。。

时间一点一点地过去，突然我又发现好像可以用另一种贪心的方法来做，先把所有产品按照利润从大到小排序，然后这个把这个放在截止日期那天卖出，并做好标记，如果截至日期那天已经有其他产品占用了，那么可以把这个产品卖出的时间往前推，直到找到可以卖的那一天并标记好。 按照这种思路提交，AC了，不过却用了141 ms。

用了这个方法之后，再回想了下并查集方法的代码， 瞬间恍然大悟， 所谓的用并查集做，实际上是对上面那种方法的优化！

用并查集的关键之处是，我们知道按照上面那个方法，假设一个产品a占用了一个日期后，那么如果下次又有一个产品b和产品a的截止日期是相同的，但是那个日期以被占用了，所以就要往前移动1天，那么就可以用并查集进行标记，在a占用了那个日期后，把a的截止日期指向前一个日期，这样的话，可以直接查找到他要占用到哪一个时间。  用了并查集优化后，时间为47MS。

代码：

1. 贪心+优先队列

#include
#include
#include
using namespace std;

const int N = 10005;
struct Node{
    int px, dx;
    friend bool operator<(const Node&a,const Node&b){
        return a.dx>b.dx;
    }
}arr[N];

priority_queue,less >q;

int n;

int main(){
    while(~scanf("%d",&n)){
        int maxTime=0;
        for(int i=0; imaxTime) maxTime = arr[i].dx;
        }
        sort(arr,arr+n);
        int ans = 0, pos=0;;
        while(!q.empty()) q.pop();
        for(int t=maxTime; t>=1; --t){
            while(pos=t){
                q.push(arr[pos++].px);
            } 
            if(!q.empty()){
                ans += q.top();
                q.pop();
            }
        }
        printf("%d\n", ans);
    }
    return 0;
}

2. 另一种贪心方式（无并查集优化）

#include
#include
#include
#include
using namespace std;

const int N = 10005;
struct Node{
    int px, dx;
    friend bool operator<(const Node&a,const Node&b){
        return a.px>b.px;
    }
}arr[N];

int n;

int main(){
    while(~scanf("%d",&n)){
        int maxTime=0;
        for(int i=0; imaxTime) maxTime = arr[i].dx;
        }
        sort(arr,arr+n);
        bool vis[N];
        memset(vis, 0, sizeof(vis));
        int ans = 0, pos=0;
        for(int i=0; i=1; --j)if(!vis[j]){
                    ans += arr[i].px;
                    vis[j] = true;
                    break;
                }
            }
        }
        printf("%d\n", ans);
    }
    return 0;
}

3. 并查集优化

#include
#include
#include
#include
using namespace std;

const int N = 10005;
struct Node{
    int px, dx;
    friend bool operator<(const Node&a,const Node&b){
        return a.px>b.px;
    }
}arr[N];

int f[N],rank[N],n;
inline void init(int n){
    for(int i=0; i<=n; ++i)
        f[i]=i, rank[i]=0;
}
int find(int x){
    int i, j=x;
    while(j!=f[j]) j=f[j];
    while(x!=j){
        i=f[x]; f[x]=j; x=i;
    }
    return j;
}

int main(){
    while(~scanf("%d",&n)){
        int maxTime=0;
        for(int i=0; imaxTime) maxTime = arr[i].dx;
        }
        init(maxTime);
        sort(arr,arr+n);
        bool vis[N];
        int ans = 0, pos=0;
        for(int i=0; i0){
                ans += arr[i].px;
                f[d] = d-1;
            }
        }
        printf("%d\n", ans);
    }
    return 0;
}

——  生命的意义，在于赋予它意义。

          

     原创 http://blog.csdn.net/shuangde800 ， By   D_Double  (转载请标明)