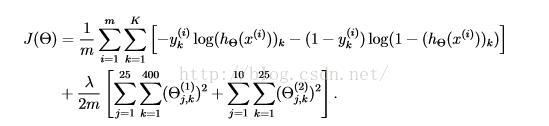Neural Network ：Backpropagation的实现

前段时间说决定要深入学习机器学习这方面，但后来从外面接了个android项目，又忙着搞着java的课程设计，没有怎么专注学习机器学习这块。确实发现自己还是没能沉下心来认真的做一件事，这方面需要改正。最近一些感想定到11月16日分享一下。

   

    回到正题，我们的神经网络的反向传播算法。

   

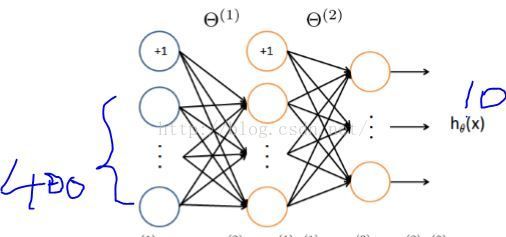
    跟着实验的指导书我在前面预先实现了一个三层神经网络的手写数字识别的网络，前面一篇博文也略有提到，这里不再赘述，如果需要实验相关资料的可以私信我，我看到会及时发给大家。（我也是个小白，不要要求太高）

                 

    要训练这个神经网络我们大概的步骤如下：

    ①、随机初始化神经元的权值theta。

    ②、获取训练样本，通过神经网络计算结果。

    ③、根据计算的结果与样本中正确的结果计算代价。

    ④、根据代价函数去梯度下降寻找最适的权值。

    然后这样重复迭代，就可以达到训练的目的。

    ①我们先来进行第一步：随机初始化theta,

    对于这个三层神经网络，theta应该有两层（1、2层之间的theta1;2、3层之间的theta2)

    对theta1来说，第一层我们称之为input_layer,第二层称之为out_layer,

    我们注意到对于input_layer 是需要增加一个偏置单元（？）

   

    先初始化temp为0

    temp = zeros(out_layer_size,1+input_layer_size);

    接下来就是随机初始化，不错初始化的值也是很讲究的。指导书说初始化的权值在[-0.12,0.12]之间时使得学习更有效率。

    init = 0.12;

    temp = rand(out_layer_size,1+input_layer_size) * 2 * init - init;

    rand()函数会随机生成一个（0，1）之间的数，通过上边的式子就可以保证区间是我们想要的，然后rand(m,n)函数会返回一个matrix[m,n];

    至此，随机初始化的步骤我们就完成了。

   

    ②下面一步该是我们的通过样本计算预测结果。

    首先，怎么获取我们的样本呢？

    注意到样本数据都是一.mat的格式保存的，即它是以矩阵形式存储的， 加载数据可以直接用

    Load('data.mat');

    保存时它在哪个矩阵，Load后矩阵的名字还是它。（不需要我们把Load的赋值给一个自定义的矩阵，当然也可以赋值）。

    （假设我们已经获取到训练样本）

     X(5000,400）是5000个手写图片样本（像素 20 *20）。

     theta1（25，401）为一二层之间的权值，theta2（10，26）为二三层之间的权值。

     y为实际的结果。（因为输出单元是10个，输出结果是10维的行向量，哪一行为1，代表预测结果为几。）

     预测计算：

     m = size(X,1);%算出样本的个数为m

     p = zeros(size(X,1),1);%先来初始化返回结果5000个0，第一个样本为2则，应该值p(1,1)=2;

     h1 = sigmoid([ones(m,1) X] * theta1'];%因为加了偏置单元，所以要多加一列。

     h2 = sigmoid([ones(m,1) h1]*hteta2'); %同样加了偏置单元

                                           %h2为一个5000*10的矩阵，记录了每个样本在每个单元的输出。

     [dummy,p] = max(h2,[],2);             %2打表求矩阵中每一行的最大值，p是记录位置的矩阵。

     sigmoid函数

     

function g = sigmoid(z)
%SIGMOID Compute sigmoid functoon
%   J = SIGMOID(z) computes the sigmoid of z.

g = 1.0 ./ (1.0 + exp(-z));
end

     这样就产生一个预测值。

     ③计算代价

      首先我们要知道使用的代价函数是什么

      这是正则化的代价函数。（先姑且不讨论为什么这么定义,以及正则化的思路）

             

    

    h（theta) 即我们说的sigmoid()函数

    实现代码：

   

a1 = [ones(m,1) X];   
z2 = Theta1 * a1';   
a2 = sigmoid(z2);   
a2 = [ones(1,m); a2];  
z3 = Theta2 * a2;   
a3 = sigmoid(z3);  
y_vect = zeros(num_labels, m);   
for i = 1:m,   
    y_vect(y(i),i) = 1;   
end;  
for i=1:m,   
    J+=sum(-1*y_vect(:,i).*log(a3(:,i))-(1-y_vect(:,i)).*log(1-a3(:,i))); 
end;   
J = J/m;  
J = J + lambda*(sum(sum(Theta1(:,2:end).^2))+sum(sum(Theta2(:,2:end).^2)))/2/m;

                            

    计算完预测的代价，我们便可以开始进行第四步。修正我们的权值

    在这之前你需要了解：

        1、sigmoid假设记为g(x)的话，那么它的导数为 g'(x) = g(x)(1-g(x));

        2、假设我们把第i层的误差记为delta(i)的话，那么输出层delta(i) = a(i) - y;(a(i)为预测的输出，y中 的元素值为{0，1}；隐藏层中delta(i) = theta(i)'*delta(i+1)*g'(z(i));（可以看上图理解这些参数。）

        3、经过一轮（所有样本计算一遍）后，我们要计算出一个Delta(i)即总体的一个修正值（可理解为要下降的梯度值）Delta(i) = Delta(i) + delta(i+1)*a(i)';("'"在这里是矩阵转置的意思）。这个Delta是所有样本累计的梯度值，

        4，所以我们要除以样本个数，因为我们取均值似乎更合理，总比用总值强，况且我们预测也是一个样本一个样本预测，所以必须除以样本个数。

        5，对于正则化的神经网络，求出梯度后还应对梯度做这样的处理

                                  

      接下来就是实现的代码，为了方便，我直接贴整个文件的代码     

  function [J grad] = nnCostFunction(nn_params, ...
                                   input_layer_size, ...
                                   hidden_layer_size, ...
                                   num_labels, ...
                                   X, y, lambda)
%NNCOSTFUNCTION Implements the neural n+fication
%   [J grad] = NNCOSTFUNCTON(nn_params, hidden_layer_size, num_labels, ...
%   X, y, lambda) computes the cost and gradient of the neural network. The
%   parameters for the neural network are "unrolled" into the vector
%   nn_params and need to be converted back into the weight matrices. 
% 
%   The returned parameter grad should be a "unrolled" vector of the
%   partial derivatives of the neural network.
%

% Reshape nn_params back into the parameters Theta1 and Theta2, the weight matrices
% for our 2 layer neural network
Theta1 = reshape(nn_params(1:hidden_layer_size * (input_layer_size + 1)), ...
                 hidden_layer_size, (input_layer_size + 1));

Theta2 = reshape(nn_params((1 + (hidden_layer_size * (input_layer_size + 1))):end), ...
                 num_labels, (hidden_layer_size + 1));

% Setup some useful variables


m = size(X, 1);

% You need to return the following variables correctly 
J = 0;
Theta1_grad = zeros(size(Theta1));
Theta2_grad = zeros(size(Theta2));

% ====================== YOUR CODE HERE ======================
% Instructions: You should complete the code by working through the
%               following parts.
%
% Part 1: Feedforward the neural network and return the cost in the
%         variable J. After implementing Part 1, you can verify that your
%         cost function computation is correct by verifying the cost
%         computed in ex4.m
%
% Part 2: Implement the backpropagation algorithm to compute the gradients
%         Theta1_grad and Theta2_grad. You should return the partial derivatives of
%         the cost function with respect to Theta1 and Theta2 in Theta1_grad and
%         Theta2_grad, respectively. After implementing Part 2, you can check
%         that your implementation is correct by running checkNNGradients
%
%         Note: The vector y passed into the function is a vector of labels
%               containing values from 1..K. You need to map this vector into a 
%               binary vector of 1's and 0's to be used with the neural network
%               cost function.
%
%         Hint: We recommend implementing backpropagation using a for-loop
%               over the training examples if you are implementing it for the 
%               first time.
%
% Part 3: Implement regularization with the cost function and gradients.
%
%         Hint: You can implement this around the code for
%               backpropagation. That is, you can compute the gradients for
%               the regularization separately and then add them to Theta1_grad
%               and Theta2_grad from Part 2.
% 



a1 = [ones(m,1) X];   
z2 = Theta1 * a1';   
a2 = sigmoid(z2);   
a2 = [ones(1,m); a2];  
z3 = Theta2 * a2;   
a3 = sigmoid(z3);  
y_vect = zeros(num_labels, m);   
for i = 1:m,   
    y_vect(y(i),i) = 1;   
end;  
for i=1:m,   
    J+=sum(-1*y_vect(:,i).*log(a3(:,i))-(1-y_vect(:,i)).*log(1-a3(:,i))); 
end;   
J = J/m;  
J = J + lambda*(sum(sum(Theta1(:,2:end).^2))+sum(sum(Theta2(:,2:end).^2)))/2/m; 
 
Delta1 = zeros(size(Theta1));   
Delta2 = zeros(size(Theta2));   

for i=1:m,   
    delta3 = a3(:,i) - y_vect(:,i);  
    delta2 = (Theta2'*delta3)(2:end,:).*sigmoidGradient(z2(:,i));   
    Delta2+=delta3 * a2(:,i)'; 
    Delta1+= delta2* a1(i,:);   
end;  
Theta2_grad = Delta2/m;   
Theta1_grad = Delta1/m; 
Theta2_grad(:,2:end) = Theta2_grad(:,2:end) .+ lambda * Theta2(:,2:end) / m;   
Theta1_grad(:,2:end) = Theta1_grad(:,2:end) .+ lambda * Theta1(:,2:end) / m;     










% -------------------------------------------------------------

% =========================================================================

% Unroll gradients
grad = [Theta1_grad(:) ; Theta2_grad(:)];


end

             

需要原版文件资料可以评论或私信，看到后博主会第一时间发的。

博主也是小白，一些细微的地方理解也不是非常透彻，有兴趣的可以一同讨论。

希望尊重博主劳动成果，转载注明出处，谢谢。