图像压缩论文GENERALIZED OCTAVE CONVOLUTIONS FOR LEARNED MULTI-FREQUENCY IMAGE COMPRESSION阅读笔记

原文链接：http://arxiv.org/abs/2002.10032

abstract

基于深度学习的图像压缩最近显示出优于标准编解码器的潜力。最先进的率失真（R-D）性能是通过上下文自适应熵编码方法实现的，在这种方法中，超先验和自回归模型被联合用于有效地捕获潜在表示中的空间依赖性。然而，在以前的工作中，特征图是具有相同空间分辨率的特征映射，其中包含一些影响R-D性能的冗余。在本文中，我们提出了第一种学习到的多频图像压缩和熵编码方法，该方法基于最近开发的octave卷积，将特征图分解为高频和低频（分辨率）分量，其中低频由较低的分辨率表示。因此，减少了其空间冗余，从而提高了R-D性能。新的广义octave卷积和具有内部激活层的octave转置卷积结构也被提出，以保留更多的信息空间结构。实验结果表明，在Kodak数据集上，该方案不仅在PSNR和MS-SSIM方面优于现有的所有学习方法，还优于下一代视频编码标准VVC（4:2:0）等标准编解码器。我们还表明，所提出的广义octave卷积可以提高其他基于自动编码器的计算机视觉任务的性能，如语义分割和图像去噪。

INTRODUCTION

基于深度学习的图像压缩[1,2,3,4,5,6,7,8,9,10,11,12]已显示出优于标准编解码器（如JPEG2000和基于H.265/HEVC的BPG图像编解码器）的潜力[13]。文献[10]首次使用学习图像压缩技术，使用基于长短时记忆（LSTM）的递归神经网络（RNN）对缩略图图像进行压缩，其中SSIM结果优于JPEG和WebP。这种方法在[5]中得到了推广，它利用空间自适应比特分配来进一步提高性能。

在文献[4]中，提出了一种基于广义除数归一化（GDN）和逆GDN（IGDN）的方案，该方案在峰值信噪比和SSIM方面均优于JPEG2000。[9]中提出了一种具有残差连接的压缩自动编码器框架，如ResNet中所述，其中量化被平滑近似代替，并使用缩放方法获得不同的比率。在[2]中，介绍了一种软到硬的矢量量化方法，并为图像压缩和深度学习模型压缩开发了一个统一的框架。为了考虑图像内容的空间变化，在[6]中引入了内容加权框架，其中采用了局部自适应比特率分配的重要性图。为了减小量化误差，还采用了学习的信道量化和算术编码。

在利用图像压缩框架中的其他计算机视觉任务方面也做出了一些努力。例如，在[3]中，通过利用生成对抗网络（GAN）和基于BPG的残差编码，提出了一种基于深层语义分割的分层图像压缩（DSSLIC）。在很大的比特率范围内，它在PSNR和MS-SSIM[14]方面都优于BPG编解码器（RGB444格式）。

由于大多数学习过的图像压缩方法需要为多比特率训练多个网络，因此也提出了变速率方法，其中训练单个神经网络模型以在多比特率下运行。该方法首先由[10]引入，然后在[11]中使用基于深度学习的熵编码将其推广到全分辨率图像。文献[15]中针对所有尺度优化了基于CNN的多尺度分解变换，其性能优于MS-SSIM中的BPG。在[16]中，利用位平面分解和选通单元的双向组装，提出了一种学习的渐进式图像压缩模型。[17]中引入了另一个可变rate框架，该框架采用了基于GDN的短连接、基于随机舍入的可伸缩量化和可变rate目标函数。[17]中的方法优于先前学习的可变rate方法。

大多数以前的工作使用编码器和解码器之间共享的固定熵模型。在[18]中，提出了一种基于高斯尺度混合（GSM）的条件熵模型，其中，比例参数以使用超自动编码器的超先验学习为条件。压缩后的hyperprior被传输并添加到比特流中作为旁侧信息。该模型在[7,8]中进行了扩展，其中使用了高斯混合模型（GMM），该模型的均值和标度参数均以hyperprior为条件。在这些方法中，超先验与使用上下文模型生成的自回归先验相结合，在PSNR和MS-SSIM方面都优于BPG。[8]中的编码效率在[19]中通过图像压缩和质量增强网络的联合优化得到进一步提高。[20]介绍了另一种上下文自适应方法，其中多尺度掩蔽卷积网络用于与Hyperprior相结合的自回归模型。

通过结合超先验和自回归模型的上下文自适应熵方法实现了学习图像压缩的最新技术[7]。这些方法被联合优化以有效地捕获潜在表示的空间依赖性和概率结构，从而产生具有优异率失真（R-D）性能的压缩模型。然而，与自然图像类似，潜伏期通常由具有相同空间分辨率的特征图表示，这具有一些空间冗余。例如，其中一些贴图具有更多低频分量，因此不需要与具有更多高频分量的其他贴图相同的分辨率。这表明，通过在不同的特征映射中具有不同的空间冗余，可以实现更好的R-D性能。

本文介绍了一种学习的多频（双频）图像压缩和熵模型，其中利用octave卷积[21]将潜在表示分解为高频（HF）和低频（LF）分量。LF信息随后由较低的空间分辨率表示，这减少了相应的空间冗余并提高了压缩性能，类似于小波变换[22]。此外，由于octave卷积中高频分量和低频分量之间的有效通信，重建性能也得到了改善。在原始octave卷积[21]中，固定插值方法用于向下和向上采样操作，不保留空间信息。因此，它会对图像压缩性能产生负面影响。为了在我们的图像编码框架中保留潜在的空间结构，我们开发了新的具有内部激活层的广义octave卷积和octave转置卷积结构。

实验结果表明，该方案在Kodak数据集上的PSNR和MS-SSIM性能均优于现有的基于学习的方法和标准编解码器。这项工作中提出的框架桥接了小波变换和深度学习。因此，小波变换中的许多技术可用于所提出的框架中，以进一步提高其性能。这将对未来的图像编码研究产生深远的影响。此外，我们还证明了所提出的广义octave卷积和转置卷积结构可以提高其他基于自动编码器的计算机视觉任务（如语义分割和图像去噪）的性能和计算复杂度。

2. VANILLA VS. OCTAVE CONVOLUTION

普通卷积可被表示为：

在普通卷积中，所有输入和输出特征映射都具有相同的空间分辨率。如果现有深度学习方案的每一层中的特征映射具有相同的分辨率，则将存在一些不必要的冗余，这将影响压缩等应用中的性能。例如，一些特征贴图捕获更多的低频分量，因此不需要与具有更多高频分量的其他特征贴图相同的分辨率。这表明，通过在不同的特征映射中使用不同的空间冗余，可以实现更好的R-D性能，类似于小波变换中的方法[23]。 

为了解决这个问题，在最近开发的octave卷积[21]中，特征映射被分解为具有不同分辨率的HF和LF分量，其中每个分量用不同的卷积进行处理。因此，LF特征映射的分辨率可以在空间上降低，从而节省内存和计算量。

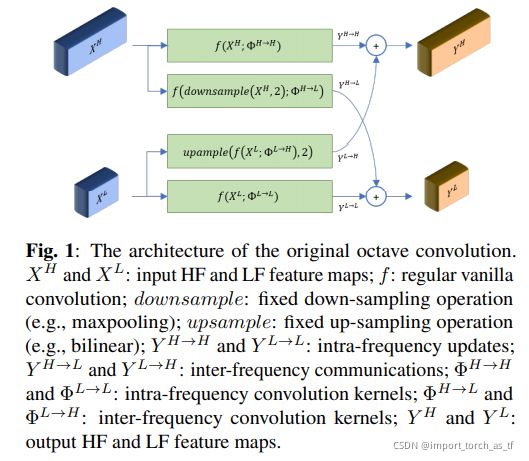
原始octave卷积的结构如图1所示。octave卷积中输入向量X的因式分解用X={XH，XL}表示，其中分别表示HF和LF映射。分配给LF特征表示（即，空间分辨率的一半）的通道比率由α∈ [0,1]定义。分解后的输出向量表示为其中，和是输出高频和低频映射。输出结果如下所示：

 

其中，代表频域内更新，代表频域间更新。频率内组件用于更新每个部件内的信息，而频率间通信进一步实现了两个部件之间的信息交换。与滤波器组理论[24]类似，octave卷积允许HF和LF特征映射之间的信息交换。

octave卷积核由Φ = [ΦH,ΦL]给出，输入XH和Xl分别与之卷积。ΦH和ΦL进一步分为频率内和频率间分量，如下所示：

 对于频率内更新，使用常规的卷积。然而，上下采样插值用于计算频率间通信，公式如下：

其中f表示参数Φ的普通卷积。

如[21]中所述，由于有效的频率间通信，octave卷积在分类和识别性能方面比普通卷积具有更好的性能。由于octave卷积允许在HF和LF特征映射中使用不同的分辨率，因此非常适合图像压缩。这促使我们将其应用于学习过的图像压缩。但是，为了获得良好的性能，需要进行一些修改。 

 3. GENERALIZED OCTAVE CONVOLUTION

在原始octave卷积中，平均池和最近插值分别用于频率间通信中的下采样和上采样操作[21]。这样的传统插值不保留输入特征地图的空间信息和结构。此外，在卷积的自动编码器中，下采样操作需要在解码器中反转，池化等固定操作会导致性能不佳 [25]。

 在这项工作中，我们提出了一种新的广义octave卷积（GoConv），其中使用跨步卷积对特征向量进行下采样，并以更有效的方式计算频率间通信。固定的下采样操作（如池化）旨在忘记空间结构，例如，在对象识别中，我们只关心对象的存在或不存在，而不关心其位置。然而，如果空间信息很重要，跨步卷积可以是一种有用的替代方法。通过学习滤波器，跨步卷积可以学习处理跨步产生的不连续性，并保留下采样操作所需的更多空间特性[25]。此外，由于它可以学习如何总结，因此可以更好地概括输入。因此，可以在更少空间信息丢失的情况下实现更好的性能，特别是在自动编码器中，在自动编码器中更容易反转跨步卷积。此外，与在ResNet中一样，与紧跟固定下采样操作（例如，平均池）的卷积相比，应用跨步卷积（即，卷积和下采样同时进行）降低了计算成本。（跨步卷积替换池化来下采样）

 拟议GoConv的架构如图2a所示。与原始octave卷积（图1）相比，我们对频率间卷积运算的输入进行了另一个重要的修改。如第2节所述，为了计算频率间通信输出（）输入HF和LF矢量（由XH和XL表示）分别被视为HF-to-LF和LF-to-HF卷积的输入(f↓2and g↑2in Figure 2a)。该策略仅在步长为1时有效（即，输入和输出HF和LF向量的大小相同）。然而，在GoConv中，此过程可能导致较大步幅的重大信息丢失。作为一个例子，考虑使用步幅2，这导致下采样输出HF和LF特征映射（输入HF和LF映射的半分辨率）。为了实现这一点，频率内卷积需要跨步2（图2a中的f）。然而，对于频率间卷积f↓2、应使用4的苛刻步幅，这会导致严重的空间信息损失。

 为了解决这个问题，我们使用两个连续的步长为2的卷积，其中第一个卷积实际上是频率内操作f。换句话说，为了计算，我们利用f学习的过滤器来减少信息损失。因此，我们设置代替作为的输入。（为实现高频特征和低频特征的信息交换，需要用上采样和下采样操作来进行连接）

GoConv中的输出高频和低频特征映射公式如下：

其中f↓2和g↑2分别是步长为2的普通卷积和转置卷积运算。 

在原始octave卷积中，激活层（如ReLU）应用于输出HF和LF映射。然而，如图2所示，我们在建议的GoConv中对每个内部卷积进行激活。在这种情况下，我们确保激活函数被正确地应用于通过卷积运算计算的每个特征映射。每个频率间和频率内分量之后是GoConv中的激活层。

 我们还提出了一种广义的倍频程转置卷积，用GoTConv表示（图2），它可以取代深度自动编码器（编码器-解码器）架构中常用的传统转置卷积。设分别为分解后的输入和输出特征向量，GoTConv中的输出HF和LF映射可被表示为：

 

 与使用常规卷积运算的GoConv不同，g表示的转置卷积用于GoTConv中的频率内更新。对于频率间通信中的上下采样操作，相同的跨步卷积与GoConv中的相同，分别使用。（GoConv的转置运算）

 与原来的octave卷积类似，所提出的GoConv和GoTConv被设计和表述为通用的即插即用单元。因此，它们可以分别取代任何卷积神经网络（CNN）架构中的普通卷积和转置卷积单元，特别是基于自动编码器的框架，如图像压缩、图像去噪和语义分割。在自动编码器中使用时，编码器的输入图像不表示为多频张量。在这种情况下，为了计算编码器中第一GoConv层的输出，等式4修改如下：（第一层和最后一层需要特殊的处理来分解和融合高频低频特征）

 

 类似地，在解码器端，最后一个GoTConv的输出是一个张量表示，可以用修正的方程5表示：

与GoConv相比，GoTConv中每个内部转置卷积使用激活的过程是反向的，激活层后面是频率间和频率内通信，如图2所示。