【算法浅析NO.00004】递归算法浅析（un-accomplished version） by arttnba3

0x00.绪论

递归算法或许是学习算法时最先碰到的基础算法了，或许大部分人都会像我当年一样看一两眼、知道“哦递归就是函数自己调用自己嘛”就跳过了，便缺少了对递归的应用的深入理解，后面遇到需要应用递归算法时只好重新翻回来看书上的例程…

而今天之所以要写这篇博文，实际上是因为看到了一道有意思的题目，于是想来重新谈一谈递归这一个看似仅仅是“入门级”的算法

PS1:最近博文更新速度慢是因为要备战段考啦
PS2:企鹅大佬的博客依然保持两三天一篇高水准博客的水平，太强大了，膜拜…
PS3:本篇博文其实本质上是习题集，毕竟只有通过实例才能更好的理解一种算法

0x01.什么是递归（recursion）？

顾名思义^{（好像也不能顾名思义…）}，递归算法即为程序调用自身的一种特殊算法，通常在OI当中的实现是函数调用自身，通过一层一层的递归来解决一个实际问题

递归算法的本质是一种通过重复将问题分解为同类的子问题而解决问题的方法

递归算法常见的形式如下：

ElementType Function(ElementType Element)
{
	Statement;//selectable
	return Element;//r1,element has been handled,selectable when the r3 sxisted
	Statement;//selectable
	return Statement with Function(Element);//r2,element has been handled,statement is selectable
	Statement;//selectable
	return Element;//r3,element has been handled,selectable when the r1 existed
}

0x02.递归算法的简单应用-part1

递归算法能够解决的问题：
1.数据的定义是按递归定义的。如Fibonacci函数。
2.问题解法按递归算法实现。如Hanoi问题。
3.数据的结构形式是按递归定义的。如二叉树、广义表等。
（百度百科：递归算法）

我一直觉得，纯粹的定义是苍白的，只有将一个算法真正地应用到实例当中，才能更好的让人理解它

所以下面都是习题集

一、求阶乘

阶乘是什么就不需要我多说了⑧
求一个数的阶乘可以通过递归很方便的进行实现：

int factorial(int n)
{
	if(n==0||n==1)
		return 1;
	return factorial(n-1)*n;
}

二、汉诺塔问题

汉诺塔：汉诺塔（又称河内塔）问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

（百度百科：汉诺塔）

描述
约19世纪末，在欧州的商店中出售一种智力玩具，在一块铜板上有三根杆，最左边的杆上自上而下、由小到大顺序串着由64个圆盘构成的塔。目的是将最左边杆上的盘全部移到中间的杆上，条件是一次只能移动一个盘，且不允许大盘放在小盘的上面。
这是一个著名的问题，几乎所有的教材上都有这个问题。由于条件是一次只能移动一个盘，且不允许大盘放在小盘上面，所以64个盘的移动次数是：18,446,744,073,709,551,615
这是一个天文数字，若每一微秒可能计算(并不输出)一次移动，那么也需要几乎一百万年。我们仅能找出问题的解决方法并解决较小N值时的汉诺塔，但很难用计算机解决64层的汉诺塔。

假定圆盘从小到大编号为1, 2, …

输入
输入为一个整数后面跟三个单字符字符串。 整数为盘子的数目，后三个字符表示三个杆子的编号。
输出
输出每一步移动盘子的记录。一次移动一行。 每次移动的记录为例如 a->3->b 的形式，即把编号为3的盘子从a杆移至b杆。
样例输入
2 a b c
样例输出
a->1->c
a->2->b
c->1->b
（OpenJudge6261-汉诺塔问题）

汉诺塔问题可以说是在学习递归算法时最为经典的例题了，无论在哪一本算法书上，讲到递归算法时必然会提到这个有趣的塔，这里我们便以open judge上的这道例题进行讲解

我们可以看到，在移动盘子时，我们需要将所有盘子从A塔移动到C塔，但是盘子是从小到大、从上往下摆放的，小的盘子不能放在大的盘子的下面，于是我们需要用到B塔作为中介以临时摆放一些盘子

例如说搬两个盘子，我们用数字大小代表盘子大小，我们可以：

将盘1从A移动至B
将盘2从A移动至C
将盘1从B移动至C

不难看出，我们可以将这个问题简化成：

将N-1个盘子从A移动至B
将第N个盘子从A移动至C
将N-1个盘子从B移动至C

那么，我们的递归函数也就很好写出来了：

int hanoi(char a, char b, char c, int n)//from a to c
{
	if(n==1)
		cout<<a<<"->"<<n<<"->"<<c<<endl;
	else
	{
		hanoi(a,c,b,n-1);
		cout<<a<<"->"<<n<<"->"<<c<<endl;
		hanoi(b,a,c,n-1);
	}
}

三、输出字符三角形

描述
有一种按规律组成的三角形，如下所示：
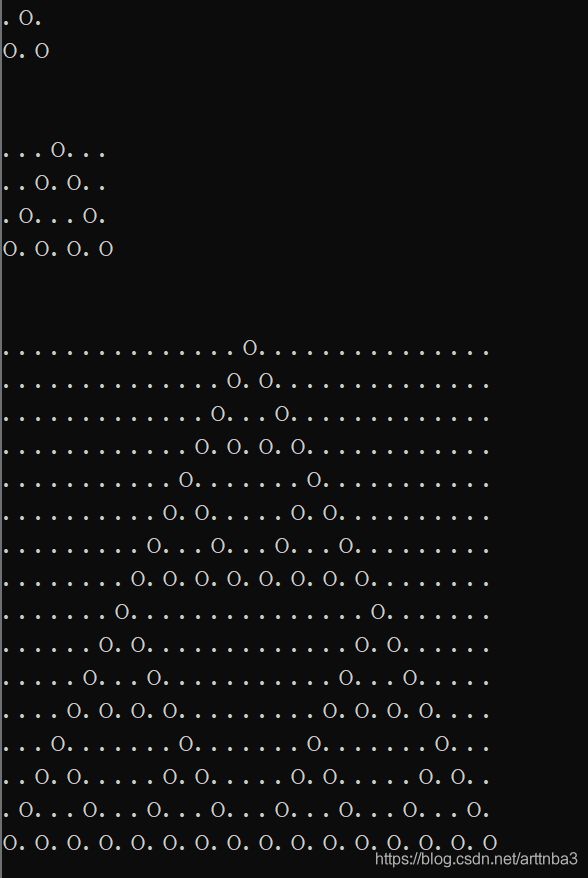
第一级三角形
第二级三角形
第三级三角形
输入
输入为两行：
第一行为输出的特殊三角形的个数N，N∈[1,20]
第二行为每一个三角形的级数M，M∈[1,8]
输出
按照级数从小到大的顺序将N个三角形输出，每个三角形之间间隔两行
样例输入
3
4 1 2
样例输出

对图上的样例进行分析，我们不难看出，每一个N级的特殊三角形都由三个N-1级的特殊三角形组成，我们只需要使用递归的方式便可以制作出这样的三角形

为了输出的方便，我们可以设置一个二维数组，每次输出前将其用memset()以’.'重新填充，并利用递归的方式放置好三角形

代码如下：

void setT(char (*ch)[550],int n,int x,int y)
{
	if(n!=1)
	{
		setT(ch,n-1,x,y);//up
		setT(ch,n-1,x-twoC(n-1),y+twoC(n-1));//left
		setT(ch,n-1,x+twoC(n-1),y+twoC(n-1));//right
	}
	else
	{
		ch[y][x]='o';
		ch[y+1][x-1]='o';
		ch[y+1][x+1]='o';
	}
}

int twoC(int n)
{
	if(n==0)
		return 1;
	else if (n==1)
		return 2;
	return 2*twoC(n-1);
}

四、二叉树的遍历

详见：https://blog.csdn.net/arttnba3/article/details/102469343

五、逆转链表

详见：https://blog.csdn.net/arttnba3/article/details/102907992

六、未完待续…