算法设计与分析-时间和空间的权衡
引入问题:
考虑一个计算函数值的问题:
你可以完全不用任何计算方法,先把函数值计算好(例如计算三角函数的值的那张表),把这些预先就计算好了的值存储于计算机中,当你需要这个函数值时,直
接去取就行了,当然这样的时间复杂度是O(1),因为你不需要任何计算,直接取出即可。(在计算机发明之前,事实上就是这样,类似于三角函数查表)
相对于其他再用别的算法来计算函数值的算法,它的时间复杂度是最好滴,它是最快滴。当然,你为时间最快付出了什么代价呢?空间!对,你需要一块空间来存
储这些值,而其他的算法不需要或者需要的空间少得多。
这就是时间和空间的考量,有时候需要拿时间换取空间,有时候需要拿空间换取时间。
在一些算法设计中,上面这个很简单的问题给了我们一些启示, 拿空间换取时间 !!!
--------------------------------------------------------------------------------------------------------------------------------------------------
1,按照上述问题的启发,我们有一种这样的方法,叫 输入增强 : 对部分或全部输入作预处理,获得额外的信息进行存储 ,以加速后面问题的求解。
简单的说,输入增强就是我们得到输入的时候,要不仅仅得到属于,还要对这个输入作一番处理和考察,得到它内在的更多信息,把它存起来:
1)计数排序
2)增强的字符串匹配算法:BM算法,KMP算法等都是基于这样的思想
2,另一种用空间换取时间的技术是 使用额外的空间来实现更快和更方便的数据存取 ,称为 预构造 :
1)散列法(hash表)
2)B树索引
3,还有一种空间换时间思想的技术:动态规划,将作为一门专门的算法设计技术在下一章讨论。
---------------------------------------------------------------------------------------------------------------------------------------------------
1,计数排序
思想很简单: 确定每个元素在数组中比它小的元素有多少个 ,实际就得到了每个元素的位置。若在数组A中,比元素x小的元素有2个,那么x应该是A的第三个元素即A[2]。2个循环就能得到每个元素比它小的元素有多少个,很简单,我们把这个信息存起来在另一个数组Count中,就可以根据Count的值得到它在A中的位置:
实现起来比较简单:

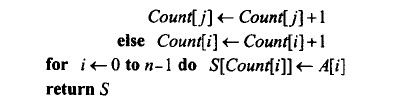
时间复杂度是n^2。
运行结果:
7
---------------------------------------------------------------------------------------------------------------------------------------------------
3, B树
i)概念和结构
又是一个比较难的结构。用来做索引用滴:
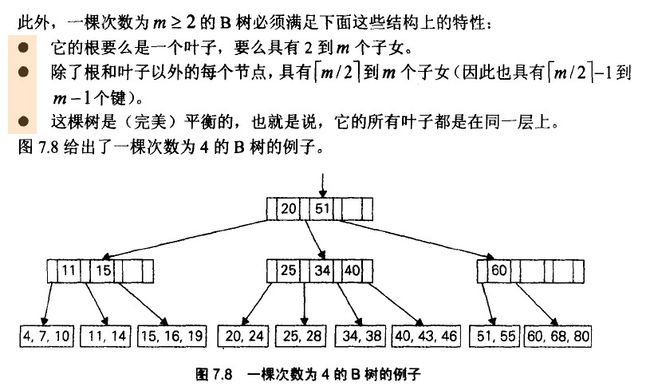
注意 n阶B树是指每个节点至多n个孩子(即每个节点至多n-1个元素)
1)如果是4阶B树(如上图),那么每个节点最多3个元素(本例中根节点也可以是3个元素),每个节点的子树最多4个。
第一条从根里元素个数的角度也可以这么说:它的根包含1到m-1个元素(与:它的根有2到m个子女等价)
2)除根和叶子外的节点至少要有m/2上取整个元素(这是规定)
3)完美平衡。( 想想是怎么进行插入,删除操作滴,才能使它完美平衡- --所有叶子在同一层上)
ii) B树上进行的操作:
1)查询
类似于二叉查找树,时间复杂度log(n)。查询不是很难,难的是插入和删除
2)插入
插入可能会导致某个节点的元素个数已满,要节点分裂
3)删除
更复杂了,参见算法导论
插入和删除的时间复杂度也是log(n)。关于B树,很复杂,在算法导论中再来好好地学习一下,算法导论花了一章的篇幅专门讨论B树,这本书上讲的还是太浅显了,先在这了解下B树的结构,大概知道B树的查询,插入,删除操作都是怎么进行滴,它们的复杂度都是log(n)
--------------------------------------------------------------------------------------------------------------------------------------------------
总结:
先就写这么多吧,这章内容比较散,主要要知道:
输入增强技术(计数排序,增强的字符串匹配等)
预构造技术(B树,hash表),B树非常复杂,先了解下它的结构,有机会好好看看算法导论
hash表非常重要,放在下一篇文章中专门来说。
考虑一个计算函数值的问题:
你可以完全不用任何计算方法,先把函数值计算好(例如计算三角函数的值的那张表),把这些预先就计算好了的值存储于计算机中,当你需要这个函数值时,直
接去取就行了,当然这样的时间复杂度是O(1),因为你不需要任何计算,直接取出即可。(在计算机发明之前,事实上就是这样,类似于三角函数查表)
相对于其他再用别的算法来计算函数值的算法,它的时间复杂度是最好滴,它是最快滴。当然,你为时间最快付出了什么代价呢?空间!对,你需要一块空间来存
储这些值,而其他的算法不需要或者需要的空间少得多。
这就是时间和空间的考量,有时候需要拿时间换取空间,有时候需要拿空间换取时间。
在一些算法设计中,上面这个很简单的问题给了我们一些启示, 拿空间换取时间 !!!
--------------------------------------------------------------------------------------------------------------------------------------------------
1,按照上述问题的启发,我们有一种这样的方法,叫 输入增强 : 对部分或全部输入作预处理,获得额外的信息进行存储 ,以加速后面问题的求解。
简单的说,输入增强就是我们得到输入的时候,要不仅仅得到属于,还要对这个输入作一番处理和考察,得到它内在的更多信息,把它存起来:
1)计数排序
2)增强的字符串匹配算法:BM算法,KMP算法等都是基于这样的思想
2,另一种用空间换取时间的技术是 使用额外的空间来实现更快和更方便的数据存取 ,称为 预构造 :
1)散列法(hash表)
2)B树索引
3,还有一种空间换时间思想的技术:动态规划,将作为一门专门的算法设计技术在下一章讨论。
---------------------------------------------------------------------------------------------------------------------------------------------------
1,计数排序
思想很简单: 确定每个元素在数组中比它小的元素有多少个 ,实际就得到了每个元素的位置。若在数组A中,比元素x小的元素有2个,那么x应该是A的第三个元素即A[2]。2个循环就能得到每个元素比它小的元素有多少个,很简单,我们把这个信息存起来在另一个数组Count中,就可以根据Count的值得到它在A中的位置:
实现起来比较简单:

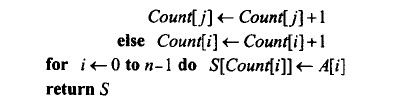
时间复杂度是n^2。
package
Section7;
/* 第七章 时空权衡 输入增强:计数排序 */
public class CountingSort {
/**
* @param args
*/
public static void main(String[] args) {
// TODO Auto-generated method stub
int [] num = { 3 , 15 , 21 , 9 , 14 , 16 , 8 , 2 , 29 , 24 , 3 , - 2 , 65 , 28 };
CountingSort(num);
for ( int i = 0 ;i < num.length;i ++ )
System.out.print(num[i] + " " );
}
public static void CountingSort( int [] num){
// 计数排序:统计每个数组元素比它小的元素有多少个,根据这个确定它在有序数组中的位置
int [] Count = new int [num.length];
for ( int i = 0 ;i < Count.length;i ++ )
Count[i] = 0 ;
for ( int i = 0 ;i < num.length - 1 ;i ++ )
for ( int j = i + 1 ;j < num.length;j ++ )
{
if (num[i] < num[j])
Count[j] ++ ;
else
Count[i] ++ ;
}
int [] result = new int [Count.length];
for ( int i = 0 ;i < Count.length;i ++ )
result[Count[i]] = num[i];
for ( int i = 0 ;i < num.length;i ++ )
num[i] = result[i];
}
}
/* 第七章 时空权衡 输入增强:计数排序 */
public class CountingSort {
/**
* @param args
*/
public static void main(String[] args) {
// TODO Auto-generated method stub
int [] num = { 3 , 15 , 21 , 9 , 14 , 16 , 8 , 2 , 29 , 24 , 3 , - 2 , 65 , 28 };
CountingSort(num);
for ( int i = 0 ;i < num.length;i ++ )
System.out.print(num[i] + " " );
}
public static void CountingSort( int [] num){
// 计数排序:统计每个数组元素比它小的元素有多少个,根据这个确定它在有序数组中的位置
int [] Count = new int [num.length];
for ( int i = 0 ;i < Count.length;i ++ )
Count[i] = 0 ;
for ( int i = 0 ;i < num.length - 1 ;i ++ )
for ( int j = i + 1 ;j < num.length;j ++ )
{
if (num[i] < num[j])
Count[j] ++ ;
else
Count[i] ++ ;
}
int [] result = new int [Count.length];
for ( int i = 0 ;i < Count.length;i ++ )
result[Count[i]] = num[i];
for ( int i = 0 ;i < num.length;i ++ )
num[i] = result[i];
}
}
-2 2 3 3 8 9 14 15 16 21 24 28 29 65
该算法的时间复杂度和简单排序一样,体现不出优势,但当数组待排序元素满足如下特征时,它的时间复杂度是线性滴:数组A的元素全部来自于一个已知大小的集合,例如已知一个数组中的元素全部是{10,11,13,15,17},根据上面的思想,只需扫描一遍数组统计每个元素出现的次数即可将数组A排好序,这种方式叫分布计数,实现也比较简单,就不写出来了。
------------------------------------------------------------------------------------------------------------------------------------------------
2,字符串匹配中的输入增强计数
1)KMP
前面写过的KMP算法实际就是一种输入增强计数,用next[]数组存储模式串的局部信息。见前面文章
2)Horspool算法
其实都差不多,什么KMP,Horspool,B-M,都是在改进匹配失败后的移动距离,而这个改进是根据模式串自身的一些特征所带来的信息(例如KMP中next数组)。
这些移动什么的都比较麻烦,写了一个Horspool,直接贴出来,想仔细了解的直接再看书:
注意,我还是照着这个思想(匹配失败时,该移动多少)写的,但并没有去存储移动多少的数组,而是每次去计算。
package
Section7;
/* 第5章 时空权衡 Horspool算法 */
public class Horspool {
/**
* @param args
*/
public static void main(String[] args) {
// TODO Auto-generated method stub
int index = HorspoolMatching( " gacd " , " dfgacfdgacdefdcd " );
System.out.println(index);
}
public static int HorspoolMatching(String p,String S){
// 返回模式串在S中的位置,如果没有返回-1
int m = p.length(); // 模式串的长度
int n = S.length(); // 匹配串的长度
int last = m - 1 ; // 用last来记录在匹配串中的位置
while (last < n - 1 )
{
if (p.equals(S.substring(last + 1 - m, last + 1 )))
return last - (m - 1 );
else
last = last + Move(S.charAt(last),p);
}
return - 1 ;
}
private static int Move( char c,String p){
// 若S和模式串匹配失败(此时S串与模式串对准的最后一个字符是c),那么返回应该移动的距离
int m = p.length();
for ( int i = m - 2 ;i >= 0 ;i -- )
if (p.charAt(i) == c)
return (m - 1 - i);
return m;
}
}
/* 第5章 时空权衡 Horspool算法 */
public class Horspool {
/**
* @param args
*/
public static void main(String[] args) {
// TODO Auto-generated method stub
int index = HorspoolMatching( " gacd " , " dfgacfdgacdefdcd " );
System.out.println(index);
}
public static int HorspoolMatching(String p,String S){
// 返回模式串在S中的位置,如果没有返回-1
int m = p.length(); // 模式串的长度
int n = S.length(); // 匹配串的长度
int last = m - 1 ; // 用last来记录在匹配串中的位置
while (last < n - 1 )
{
if (p.equals(S.substring(last + 1 - m, last + 1 )))
return last - (m - 1 );
else
last = last + Move(S.charAt(last),p);
}
return - 1 ;
}
private static int Move( char c,String p){
// 若S和模式串匹配失败(此时S串与模式串对准的最后一个字符是c),那么返回应该移动的距离
int m = p.length();
for ( int i = m - 2 ;i >= 0 ;i -- )
if (p.charAt(i) == c)
return (m - 1 - i);
return m;
}
}
运行结果:
7
---------------------------------------------------------------------------------------------------------------------------------------------------
3, B树
i)概念和结构
又是一个比较难的结构。用来做索引用滴:

注意 n阶B树是指每个节点至多n个孩子(即每个节点至多n-1个元素)
1)如果是4阶B树(如上图),那么每个节点最多3个元素(本例中根节点也可以是3个元素),每个节点的子树最多4个。
第一条从根里元素个数的角度也可以这么说:它的根包含1到m-1个元素(与:它的根有2到m个子女等价)
2)除根和叶子外的节点至少要有m/2上取整个元素(这是规定)
3)完美平衡。( 想想是怎么进行插入,删除操作滴,才能使它完美平衡- --所有叶子在同一层上)
ii) B树上进行的操作:
1)查询
类似于二叉查找树,时间复杂度log(n)。查询不是很难,难的是插入和删除
2)插入
插入可能会导致某个节点的元素个数已满,要节点分裂
3)删除
更复杂了,参见算法导论
插入和删除的时间复杂度也是log(n)。关于B树,很复杂,在算法导论中再来好好地学习一下,算法导论花了一章的篇幅专门讨论B树,这本书上讲的还是太浅显了,先在这了解下B树的结构,大概知道B树的查询,插入,删除操作都是怎么进行滴,它们的复杂度都是log(n)
--------------------------------------------------------------------------------------------------------------------------------------------------
总结:
先就写这么多吧,这章内容比较散,主要要知道:
输入增强技术(计数排序,增强的字符串匹配等)
预构造技术(B树,hash表),B树非常复杂,先了解下它的结构,有机会好好看看算法导论
hash表非常重要,放在下一篇文章中专门来说。