决策树-CART（下）

承接上文 模型选择-CART（上），我们继续来讲 CART 算法的剪枝操作。

树剪枝

一棵树如果节点过多，则表明该模型可能对数据进行了“过拟合”。我们可通过降低决策树的复杂度来避免过拟合，最有效的手段是进行剪枝处理（pruning）。

先前在函数 choose_best_split() 中的提前终止条件，实际上在进行一种所谓的预剪枝（prepruning）操作。另一种形式的剪枝需要使用测试集和训练集，称作后剪枝（postpruning）。接下来，我们将先讨论预剪枝存在的不足之处，然后再讨论后剪枝的处理方式。

预剪枝

在构建回归树中可以发现，树构建算法 create_tree() 对输入的参数 tol_s 和 tol_n 非常敏感。我们读入一个新的数据集 ex2.txt。

my_dat2 = load_dataset('data/ex2.txt')
my_dat2 = np.mat(my_dat2)


fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(my_dat1[:, 1].tolist(), my_dat1[:, 2].tolist())
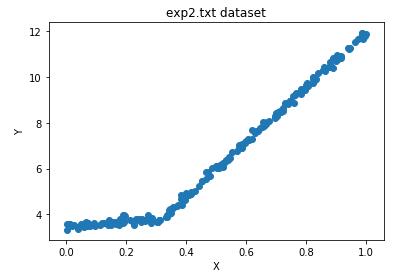
ax.set_title('ex2.txt dataset')
ax.set_xlabel('X')
ax.set_ylabel('Y')
plt.show()

该数据集与 ex00.txt 数据集非常相似，只不过 y 值的数量级大了 100 倍。我们现在仍然用对待 ex00.txt 数据集的方式去创建决策树。

>>> create_tree(my_dat2)
{'spInd': 0,
 'spVal': 0.499171,
 'left': {'spInd': 0,
  'spVal': 0.729397,
  'left': {'spInd': 0,
   'spVal': 0.952833,
   'left': {'spInd': 0,
    'spVal': 0.958512,
    'left': 105.24862350000001,
    'right': 112.42895575000001},
    // ...
    'right': {'spInd': 0,
    'spVal': 0.084661,
    'left': 6.509843285714284,
    'right': {'spInd': 0,
     'spVal': 0.044737,
     'left': -2.544392714285715,
     'right': 4.091626}}}}}

ex00.txt 数据集构建的树只有两个叶节点，而 ex2.txt 数据集构建的树却有如此之多的叶节点，这是为什么？产生这个现象的原因在于，停止条件 tol_s 对误差的数量级十分敏感。如果我们花费时间去设置 tol_s 参数的值，或许能够得到仅有两个叶节点的树。

>>> create_tree(my_dat2, ops=(10000, 4))
{'spInd': 0,
 'spVal': 0.499171,
 'left': 101.35815937735848,
 'right': -2.637719329787234}

通过不断修改停止条件来得到合理结果并不是很好的办法。事实上，我们常常甚至不确定到底需要寻找什么样的结果（要生成几个叶节点的树）。

也正是基于上述这个原因，我们需要使用后剪枝，利用测试集来对树进行剪枝。由于不需要用户指定参数，后剪枝是一个更理想化的剪枝方法。

后剪枝

使用后剪枝方法需要将数据集分成测试集和训练集。

1. 首先指定参数，使得构建出的树足够大、足够复杂，便于剪枝；
2. 接下来从上而下找到叶节点，用测试集来判断将这些叶节点合并是否能降低测试误差。如果是的话就合并。

【伪代码】：

基于已有的树切分测试数据：
    如果存在任一子集是一棵树，则在该子集递归剪枝过程
    计算将当前两个叶节点合并后的误差
    计算不合并的误差
    如果合并会降低误差的话，就将叶节点合并

is_tree()

is_tree() 函数用于测试输入变量是否是一棵树，返回布尔类型的结果。换句话说，该函数用于判断当前处理的节点是否是叶节点。

def is_tree(obj):
    return type(obj).__name__ == 'dict'

get_mean()

get_mean() 函数是一个递归函数，它从上往下遍历树直到叶节点为止。如果找到两个叶节点则计算它们的平均值。该函数对树进行塌陷处理（即返回树平均值）。

def get_mean(tree):
    if is_tree(tree['right']):
        tree['right'] = get_mean(tree['right'])
    if is_tree(tree['left']):
        tree['left'] = get_mean(tree['left'])
    return (tree['left'] + tree['right']) / 2.0

prune()

prune() 函数接受两个参数，待剪枝的树 tree 以及剪枝所需的测试数据 test_data。

def prune(tree, test_data):
    # 没有测试数据则对树进行塌陷处理
    if np.shape(test_data)[0] == 0:
        return get_mean(tree)
    if (is_tree(tree['left'])) or (is_tree(tree['right'])):
        lset, rset = bin_split_dataset(test_data, tree['spInd'], tree['spVal'])
    if is_tree(tree['left']):
        tree['left'] = prune(tree['left'], lset)
    if is_tree(tree['right']):
        tree['right'] = prune(tree['right'], rset)
    if not is_tree(tree['left']) and not is_tree(tree['right']):
        lset, rset = bin_split_dataset(test_data, tree['spInd'], tree['spVal'])
        error_no_merge = np.sum(np.power(lset[:, -1] - tree['left'], 2)) + np.sum(np.power(rset[:, -1] - tree['right'], 2))
        tree_mean = (tree['left'] + tree['right']) / 2.0
        error_merge = np.sum(np.power(test_data[:, -1] - tree_mean, 2))
        if error_merge < error_no_merge:
            print('merging')
            return tree_mean
        else:
            return tree
    else:
        return tree

• 首先确认测试集是否为空。

if np.shape(test_data)[0] == 0:
    return get_mean(tree)

• 接下来检查某个分支到底是子树还是节点。如果是子树，就调用函数 prune() 来对该子树进行剪枝。

if (is_tree(tree['left'])) or (is_tree(tree['right'])):
    lset, rset = bin_split_dataset(test_data, tree['spInd'], tree['spVal'])
if is_tree(tree['left']):
    tree['left'] = prune(tree['left'], lset)
if is_tree(tree['right']):
    tree['right'] = prune(tree['right'], rset)

• 如果左右两个分支已经不再是子树，那么就可以进行合并。具体做法是对合并前后的误差进行比较。如果合并后的误差比不合并的误差小就进行合并操作，反之则不合并直接返回。

if not is_tree(tree['left']) and not is_tree(tree['right']):
    lset, rset = bin_split_dataset(test_data, tree['spInd'], tree['spVal'])
    error_no_merge = np.sum(np.power(lset[:, -1] - tree['left'], 2)) + np.sum(np.power(rset[:, -1] - tree['right'], 2))
    tree_mean = (tree['left'] + tree['right']) / 2.0
    error_merge = np.sum(np.power(test_data[:, -1] - tree_mean, 2))
    if error_merge < error_no_merge:
        print('merging')
        return tree_mean
    else:
        return tree
else:
    return tree

在完成了后剪枝的代码后，我们再来用后剪枝的方式对 ex2.txt 数据集进行剪枝处理。

>>> my_dat_test = load_dataset('data/ex2test.txt')
>>> my_dat2_test = np.mat(my_dat_test)
>>> prune(create_tree(my_dat2), my_dat2_test)

比对两次结果，可以看到大量的节点已经被剪枝掉了，但没有像预期那样剪枝成两部分，这说明后剪枝可能不如预剪枝那般有效。一般地，为了寻求最佳模型可以同时使用两种剪枝技术。

模型树

模型树仍采用二元切分，但叶节点不再是简单的数值，取而代之的是一些线性模型或者分段线性函数。这里所谓的分段线性（piecewise linear）是指模型由多个线性片段组成。

考虑上图所示的数据集，如果使用两条直线拟合会比使用一组常数更好，而这两条直线我们可用线性模型来拟合。因为数据集里的一部分数据（0.0 ~ 0.3）以某个线性模型建模，而另一部分数据（0.3 ~ 1.0）则以另一个线性模型建模，这就是刚才说的分段线性函数。

决策树相比其他机器学习算法的优势之一在于结果更易理解。很显然，两条直线比很多节点组成一棵大树更容易解释。模型树的可解释性是它优于回归树的特点之一。另外，模型树也具有更高的预测准确度。

我们把回归树的构建代码稍加修改就可以在叶节点生成线性模型而不是常数值。难点在于误差的计算。前面用于回归树的误差计算方法在这里不能再用。现在叶节点不再是常数值，而是一个线性模型，因此我们对于给定的数据集，可以先用线性模型对数据集进行拟合，然后计算真实的目标值与模型预测值间的差值。最后将这些差值的平方求和就得到了所需的误差。

model_leaf()

model_leaf() 函数与回归树的 reg_leaf() 函数类似，当数据不再需要切分的时候负责生成叶节点的模型。该函数在数据集上调用 linear_solve() 并返回回归系数 ws。

def model_leaf(dataset):
    ws, x, y = linear_solve(dataset)
    return ws

model_err()

model_err() 函数与回归树的 reg_err() 函数类似，在给定的数据集上计算误差。该函数在数据集上调用 linear_solve()，之后返回真实值和预测值之间的平方误差。

def model_err(dataset):
    ws, x, y = linear_solve(dataset)
    y_hat = x * ws
    return np.sum(np.power(y - y_hat, 2))

linear_solve()

linear_solve() 函数的主要功能是将数据集格式化成目标变量 y 和自变量 x。x 和 y 用于执行简单的线性回归。另外，需要注意的是，如果矩阵的逆不存在会造成程序异常。

def linear_solve(dataset):
    m, n = np.shape(dataset)
    x = np.mat(np.ones((m, n)))
    y = np.mat(np.ones((m, 1)))
    x[:, 1:n] = dataset[:, 0:n-1]
    y = dataset[:, -1]
    xTx = x.T * x
    if np.linalg.det(xTx) == 0.0:
        raise NameError('This matrix is singular, cannot do inverse.\n try increasing the second value or ops')
    ws = xTx.I * (x.T * y)
    return ws, x, y

【测试代码】：

• 导入所需的数据集。

>>> my_dat3 = load_dataset('data/exp2.txt')
>>> my_dat3 = np.mat(my_dat3)

• 调用 create_tree() 函数，并将模型树相关的函数作为参数传入。

>>> create_tree(my_dat3, model_leaf, model_err, (1, 10))
{'spInd': 0, 'spVal': 0.285477, 'left': matrix([[1.69855694e-03],
         [1.19647739e+01]]), 'right': matrix([[3.46877936],
         [1.18521743]])}

可以看到 create_tree() 生成的这两个线性模型分别是 y = 3.468 + 1.1852x 和 y = 0.0016985 + 11.96477x，与用于生成该数据的真实模型非常接近。

关于本博客的所有代码，都可从 传送门 中获得。

问题

决策树如何避免过拟合？

在不考虑数据集变更的前提下，避免过拟合的手段主要是降低模型的复杂度。决策树主要有以下降低模型复杂度的方法：

• 剪枝处理
• 加入正则化项
• 限制叶结点的个数以及树的深度

sklearn 决策树调参

关于 sklearn.tree 包中的 DecisionClassifier 以及 DecisionRegressor 的相关参数以及调参方式可参考这篇博客 scikit-learn决策树算法类库使用小结

参考

• 《机器学习实战》
• scikit-learn决策树算法类库使用小结：https://www.cnblogs.com/pinard/p/6056319.html