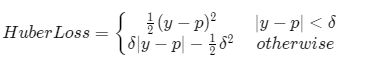Paddle框架下常用的损失函数总结
概述:
Loss是深度学习算法中重要的一部分,它的主要功能是评价网络预测的准确性和指导权重更新。合适的Loss可以让网络收敛更快,预测更准。这个示例,主要介绍了损失函数的基本概念以及7种常用的损失函数的形式、性质、参数、区别及使用场景,并给出了paddle的实现。
主要内容包括:
- L1(mean absolute error)平均绝对误差
- L2(mean square error)均方误差
- Huber Loss
- LogCosh Loss
- Cross Entropy(Log Loss)
- Focal Loss
- Hinge Loss
概念:
在深度学习算法中,需要使用一个函数来量化模型给出的预测和训练数据中的真实值之间的差异,我们把这个函数叫做Loss.形式化的,可以将Loss定义为网络预测值p和实际值y的函数L(p,y).
Loss的性质:
Loss需要满足一些性质,首先就是预测值接近真实值时Loss应该小,反之Loss应该大。其次,深度学习使用的梯度下降优化方法需要让模型权重沿着Loss导数的反向更新,所以这个函数是可导的,而且不能导数处处为0(这样权重动不了)。此外,比如MSE(均方误差)的梯度正比于Loss值,因此用MSE做训练收敛速度比一般MAE(绝对值误差)快。
Loss的分类和选择:
不同的深度学习任务输出形式不同,Loss因此也有很多种不同的选择,大致可以分为两类:回归Loss和分类Loss.回归预测的结果是连续的(比如房价),而分类预测的结果是离散的(比如手写数字识别输出是几)。在为深度学习任务选择Loss时首先要考虑的就是这个任务属于回归还是分类,虽然一些分类任务也能使用回归的Loss作为训练,但通常效果不好。确定了任务类别之后在一类Loss中选择具体的一个或几个需要结合任务中的数据和目标。
符号:
- x:训练数据集中的一个输入
- y:训练数据集中的一个输出
- p:网络针对一个输入给出的预测值
- M:分类问题中的类别数量
- N:输入loss的数据条数,可以理解为Batch Size
- i:第i条数据
- j:第j个输出
回归Loss:
Mean Absolute Error(L1 Loss)平均绝对误差和Mean Square Error(L2 Loss)均方误差。
L1平均绝对误差(MAE)和L2均方误差(MSE)是在分类任务中使用频繁的Loss.
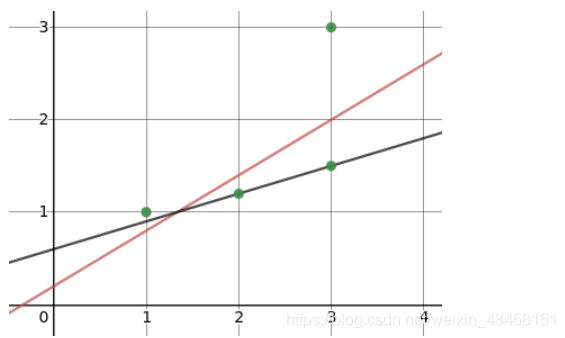
L2比L1对于数据更敏感,在网络预测值相同的情况下,如果数据1.5变成了一个离群点15,L1 Loss变大了6倍,L2 Loss变大了60倍。显然用L2 Loss拟合出的结果会对离群点更敏感。
黑线为L1的结果,红线为用L2的结果。在深度学习任务中,离群点一般代表噪声,比如医学影像中通常存在大量的椒盐噪声。但是在一些场景下有的数据点可能就是比较特殊,它们的确离群但并不是数据中的错误。如果是前者,离群点是脏数据,那么我们希望在训练的过程中降低其对 Loss 的影响,此时应该选择 L1 Loss。如果是后者,离群点是特殊情况,我们会希望考虑进这些特殊的信息,因此 L2 Loss 会更合适。
梯度
对 L1 和 L2 Loss求导可以知道 L1 Loss 的梯度一直是 ±1\plusmn 1±1,而 L2 Loss 的梯度是正比于 Loss 值的,Loss 值越大梯度越大。这一点 L2 是优于 L1 的,体现在两个方面。当Loss非常大的时候,L1的梯度一直是111,这样收敛的速度比L2慢。其次当 Loss 很接近0的时候L1的梯度还是1,这个大梯度容易让网络越过 Loss 最低点,导致 Loss 在最低点附近震荡,相比之下 L2 在 Loss 接近0的时候梯度也接近0,不存在这样震荡的问题。因此在离群点不多的前提下,希望网络更快更稳定地收敛应该选择 L2 Loss。
可微
因为L1 Loss是个分段函数,所以在最低点是不可微的。L2则全程可微,最后一定会稳定收敛到一个最优解。虽然性质上 L2 优于 L1,但是实际使用时反向传递都由框架实现,因此不影响选择。
L1和L2的选择
总体上来说L2训练收敛的速度快,选择L2的情况比较多。如果训练数据中存在比较多的脏数据应该选择L1 Loss避免其影响结果。
下面是实现:
# 初始化一些环境,这个部分下面所有Loss都会用到
import paddle.fluid as fluid
import numpy as np
places = fluid.CPUPlace()
exe = fluid.Executor(places)def l1_loss(pred, label):
loss = fluid.layers.abs(pred - label)
loss = fluid.layers.reduce_mean(loss)
return loss
l1_program = fluid.Program()
with fluid.program_guard(l1_program):
pred = fluid.data('pred', [3,1], dtype="float32")
gt = fluid.data('gt', [3,1], dtype="float32")
loss = l1_loss(pred, gt)
pred_val = np.array([[1], [2], [3] ],dtype="float32")
gt_val = np.array([[1], [3], [6] ],dtype="float32")
loss_value=exe.run(l1_program, feed={ 'pred': pred_val , "gt": gt_val },fetch_list=[loss])
print("L1 Loss:", loss_value)L1 Loss运行结果如下
def l2_loss(pred, label):
loss = (pred - label) ** 2
loss = fluid.layers.reduce_mean(loss)
return loss
l2_program = fluid.Program()
with fluid.program_guard(l2_program):
pred = fluid.data('pred', shape=[3,1], dtype='float32')
gt = fluid.data('gt', shape=[3,1], dtype='float32')
loss = l2_loss(pred, gt)
pred_val = np.array([[1], [2], [3]], dtype='float32')
gt_val = np.array([[1], [3], [6]], dtype='float32')
loss_value = exe.run(l2_program, feed={'pred': pred_val, 'gt': gt_val}, fetch_list= [loss])
print("L2 Loss:", loss_value)Mean Bias Error
![]()
MBE是不做绝对值的L1 Loss,它的一个主要问题是正负Loss会相互抵消,在深度学习的应用极少。但是因为没有做绝对值可以看出网络预测的结果是偏大还是偏小,除非有非常具体的需求,不然基本上不用MBE.
def mean_bias_error(pred, label):
loss = pred - label
loss = fluid.layers.reduce_mean(loss)
return loss
mbe_program = fluid.Program()
with fluid.program_guard(mbe_program):
pred = fluid.data('pred', shape=[3,1], dtype='float32')
gt = fluid.data('gt', shape=[3,1], dtype='float32')
loss = mean_bias_error(pred, gt)
pred_val = np.array([[3], [2], [1]], dtype='float32')
gt_val = np.array([[1], [2], [3]], dtype='float32') # 这组数据上正负的bias就抵消了,这也是深度学习基本不用这个loss的原因
loss_value = exe.run(mbe_program, feed={'pred': pred_val, 'gt': gt_val}, fetch_list= [loss])
print("MBE:", loss_value)Huber loss(Smooth L1 Loss):
注:Smooth L1 Loss 并不是Huber的别名,而是一个特殊情况。
Huber是 L1 和 L2 Loss 的分段组合。前面我们已经知道 L1 在有离群点时性能好,L2 在接近零点处稳定收敛, 于是将二者组合:在零点附近用L2,其余位置用 L1 就形成了 Huber Loss。具体的选择范围用 δ划分。 δ 取 1 的 Huber Loss 也叫 Smooth L1 Loss,所以说 Smooth L1 是 Huber 的一种情况。
分段组合克服了两个 Loss 各自的一部分弱点,Huber Loss对离群点没有 L2 敏感,在零点附近也不会出现 L1 的震荡。通过调节 δ\deltaδ 可以调节 Huber Loss 对离群点的敏感度,δ\deltaδ 越大,使用L2的区间越大,对离群点越敏感; 反之 δ\deltaδ 越小越不敏感。
如果数据中存在需要克服的离群点,但是 L1 没有达到想要的效果,可以尝试 Huber Loss,它在 Loss 很小时会带来更好的收敛。
Log-cosh:
Log-Cosh计算上先做cosh之后再做log.
Quantile Loss(分位数损失)
在一些场景(比如商业决策),用户不仅希望得到的预测值,而且希望通过一个预测区间了解预测的不确定性。这种情况下希望算法给出一个预测区间而不是单一的值。