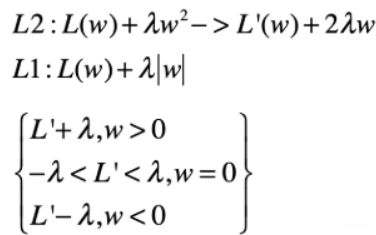逻辑回归、优化算法和正则化的幕后细节补充
1. 写在前面
今天开始, 开始尝试进行机器学习算法的一些查缺补漏知识的整理, 主要还是之前没有注意的一些点吧, 之前的一篇补充了线性回归与梯度下降算法的一些细节, 这篇文章主要是对逻辑回归算法模型的细节梳理,以及常用的两种优化算法, 包括梯度下降和拟牛顿法, 最后就是L1和L2正则。
这次梳理以重点知识为主, 白话为辅了哈哈 , 因为这些细节部分都是面试中容易出现的一些身影, 所以先初步整理一下, 到时候再简单复习回顾, 这次得严肃一点
大纲如下:
- 逻辑回归算法(要点, 来历)
- 常用的优化算法(梯度下降算法和拟牛顿法)
- 正则(L1和L2正则的区别再次梳理)
Ok, let’s go!
2. 逻辑回归算法
2.1 要点说明
逻辑回归是在线性回归的基础上加了一个 Sigmoid 函数(非线形)映射,使得逻辑回归称为了一个优秀的分类算法。本质上来说,两者都属于广义线性模型,但他们两个要解决的问题不一样,逻辑回归解决的是分类问题,输出的是离散值,线性回归解决的是回归问题,输出的连续值。
模型: 线性模型加入sigmoid函数就是逻辑回归模型, 所以理解起来就是这样:
y = s i g m o i d ( w 0 + w 1 x 1 + w 2 x 2 + . . . . w n x n ) y = sigmoid(w_0+w_1x_1+w_2x_2+....w_nx_n) y=sigmoid(w0+w1x1+w2x2+....wnxn)
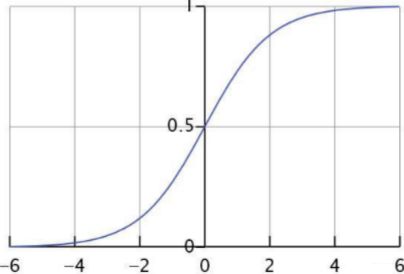
而sigmoid函数, 我们已经非常了然了吧:
o u t p u t = 1 1 + e − x output = \frac{1}{1+e^{-x}} output=1+e−x1
- 将任意input压缩到了(0, 1)之间
- 1/2处导数最大
- 如果 f ( x ) = s i g m o i d ( x ) f(x)=sigmoid(x) f(x)=sigmoid(x), 那么导数 f ( x ) ( 1 − f ( x ) ) f(x)(1-f(x)) f(x)(1−f(x))
- 两边的梯度趋于饱和(这在神经网络中是个不好的地方)
- 不以原点为中心
- 单调性
基于这几点性质, 才使得逻辑回归适合二分类问题, 上面这些是基本常识了。当然sigmoid也是有来历的, 不是凭空出来的, 后面的广义线性模型里面会提到这点。
损失函数以及由来: 关于逻辑回归的损失函数, 这里先上结论

这就是大名鼎鼎的交叉熵损失, 那么这个东西是怎么来的呢? 这个才是重点了, 哈哈。
逻辑回归模型是这样的, 它假设样本服从的是伯努利分布, 伯努利分布就是概率论里面学的多次抛硬币试验的那个, 每次试验两个结果, 每次试验互不干扰, 那么假设y_pred表示y=1的概率, 则给定X, Y的概率结果就是0和1, 如果y=1是y_pred, 那么y=0就是1-y_pred, 即下面的这个式子:
P ( Y ∣ X ) = { y − pred , y = 1 1 − y − pred , y = 0 P(Y \mid X)=\left\{\begin{array}{l} y_{-} \text {pred }, y=1 \\ 1-y_{-} \text {pred }, y=0 \end{array}\right. P(Y∣X)={ y−pred ,y=11−y−pred ,y=0
这个不用过多解释, 如果把这两个式子合并成一个, 就成了下面这个:
y − pred y ( 1 − y − pred ) 1 − y y_{-} \operatorname{pred}^{y}\left(1-y_{-} \operatorname{pred}\right)^{1-y} y−predy(1−y−pred)1−y
也就是说, 给定我一个样本, 我预测它属于某一类的概率就是上面这个式子, 注意, 这个式子里面对于某一个样本只会有一个概率, 因为y要么等于1, 要么等于0。 如果是等于1, 那么我们的预测概率是y_pred, 我们希望这个越大越好,因为他越大, 就越接近1, 而如果等于0, 我们预测概率是1-y_pred, 我们依然希望这个越大越好, 也就是说对于一个样本, 上面的这个式子越大, 我们预测的分类就会越准确。
那么多个样本呢? 就是它了:
∏ y − pred i y i ( 1 − y − pred i ) 1 − y i \prod y_{-} \operatorname{pred}_{i}^{y_{i}}\left(1-y_{-} \operatorname{pred}_{i}\right)^{1-y_{i}} ∏y−prediyi(1−y−predi)1−yi
我们依然是希望这个概率最大, 这就是极大似然的思想。 概率最大, 才说明我们的模型预测的更加准确。但是这个函数呢, 有连乘, 不太好优化, 所以取对数, 然后取负号, 就变成了loss的形式了:
- 假设样本服从的分布: 伯努利
- 损失函数的由来: 伯努利分布的极大似然估计
那么应该怎么求解参数 w w w呢?
这时候就用到了梯度下降算法。关于梯度下降算法的细节补充, 可以参考前面梳理的这个梯度下降算法的细节补充, 要明确下面几个概念:
- 梯度下降算法属于优化算法, 另外一个常见的优化算法是牛顿法
- 梯度下降法要优化的参数是w, 也就是自变量
- 梯度下降法中的“梯度”针对的是损失函数loss
下面看一下逻辑回归模型中梯度的推导过程:
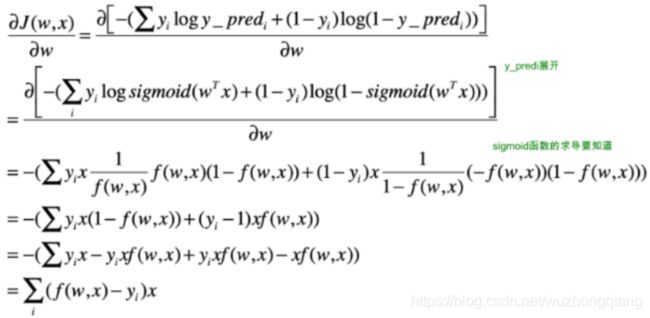
可以发现一个很有意思的事情, 竟然这个梯度等于了每一个样本的预测误差乘以样本的特征值本身。
有了参数, 就可以进行更新:
W t + 1 = W t − α ( ∑ i ( f ( w , x ) − y i ) x ) W_{t+1}=W_{t}-\alpha\left(\sum_{i}\left(f(w, x)-y_{i}\right) x\right) Wt+1=Wt−α(i∑(f(w,x)−yi)x)
关于逻辑回归, 还需要知道:
- 逻辑回归对于高维稀疏类别的特征有比较好的拟合效果
- 由于特征的稀疏性, 还间接的起到了特征选择的作用, 因为某些特征非常稀疏, 会有很多的0, 这时候, 参数的更新基本上就只更新那几个对于loss非常重要的特征, 使得w0+w1*x1…这一长串很多值都是0
- 离散化比如说对某个特征进行分桶, 这样可以增加模型的鲁棒性, 不容易被某个特征给带偏, 比较稳定, 类似于归一化
- 分桶之后, 也相当于引入了非线性
2.2 指数族分布与广义线性模型
这里算是一个拓展知识吧, 毕竟有些东西知其然, 知其所以然才有意思,我们上面埋了一个伏笔就是说sigmoid函数并不是凭空出现的, 而是有一定来历的, 那么这个东西到底是怎么来的呢?
答: sigmoid函数是又对数线性模型推过来的, 但是啥子叫对数线性模型? 在介绍这个之前, 得需要知道几率比的定义。
- 几率比: 一件事发生与不发生的概率比就是几率比, 用 p 1 − p \frac{p}{1-p} 1−pp来表示。
- 对数线性模型: 对几率比取对数后可用线性模型来表达, 即 l o g p 1 − p = w 0 + w 1 x 1 + w 2 x 2 . . . . . log \frac{p}{1-p} = w_0 + w_1x_1 + w_2x_2..... log1−pp=w0+w1x1+w2x2.....$
有了这个对数线性模型, 通过化简就可以得到sigmoid函数了:
log p 1 − p = θ T X ⇒ p 1 − p = e θ T X ⇒ p ( 1 + e θ T X ) = e θ T X ⇒ p = 1 1 + e − θ T X \begin{array}{l} \log \frac{p}{1-p}=\theta^{T} X \Rightarrow \frac{p}{1-p}=e^{\theta^{T} X} \Rightarrow p\left(1+e^{\theta^{T} X}\right)=e^{\theta^{T} X} \\ \Rightarrow p=\frac{1}{1+e^{-\theta^{T} X}} \end{array} log1−pp=θTX⇒1−pp=eθTX⇒p(1+eθTX)=eθTX⇒p=1+e−θTX1
但是突然出现了这么一个东西, 又是非常的玄幻和疑问吧, 尤其是这个对数线性模型, 为啥要取对数? 为啥取对数之后可用线性模型来表达? 感觉是在故意凑这个玩意呢? 哈哈。 下面刨根问底一下。
2.2.1 指数族分布
这个就得先从指数族分布说起, 指数族分布(The exponential family distribution),区别于指数分布(exponential distribution)。在概率统计中,若某概率 分布满足下式,我们就称之属于指数族分布
p ( y ; η ) = b ( y ) exp ( η T T ( y ) − a ( η ) ) \mathrm{p}(\mathrm{y} ; \eta)=\mathrm{b}(\mathrm{y}) \exp \left(\eta^{T} \mathrm{T}(\mathrm{y})-\mathrm{a}(\boldsymbol{\eta})\right) p(y;η)=b(y)exp(ηTT(y)−a(η))
这就是指数族分布的通式, 其中 η \eta η表示自然参数, T ( y ) T(y) T(y)是充分统计量, 一般情况下等于 y y y, e x p − α ( η ) exp^{-\alpha (\eta)} exp−α(η)起到归一化作用, 确定了 T , a , b T, a, b T,a,b我们就可以确定某个参数为 η \eta η的指数族分布了。
关于指数族分布, 典型的有: 泊松, gamma分布, beta分布, 伯努利分布, 正态分布。而逻辑回归, 我们说正好假设样本服从伯努利分布, 所以对上了哈哈。
那么为啥伯努利分布是指数族分布呢? 我们可以看看它公式的化简:
p ( y ; ϕ ) = ϕ y ( 1 − ϕ ) 1 − y = exp [ y log ϕ + ( 1 − y ) log ( 1 − ϕ ) ] = exp [ y log ϕ 1 − ϕ + log ( 1 − ϕ ) ] \begin{aligned} p(y ; \phi)=\phi^{y}(1-\phi)^{1-y} & =\exp [y \log \phi+(1-y) \log (1-\phi)] =\exp \left[y \log \frac{\phi}{1-\phi}+\log (1-\phi)\right] \end{aligned} p(y;ϕ)=ϕy(1−ϕ)1−y=exp[ylogϕ+(1−y)log(1−ϕ)]=exp[ylog1−ϕϕ+log(1−ϕ)]
这时候令
T ( y ) = y η = log ϕ 1 − ϕ a ( η ) = − log ( 1 − ϕ ) = log ( 1 + e η ) b ( y ) = 1 \begin{array}{c} T(y)=y \\ \eta=\log \frac{\phi}{1-\phi} \\ a(\eta)=-\log (1-\phi)=\log \left(1+e^{\eta}\right) \\ b(y)=1 \end{array} T(y)=yη=log1−ϕϕa(η)=−log(1−ϕ)=log(1+eη)b(y)=1
就是上面指数族分布的通式形式了。
为啥要讲这个东西呢? 首先从上面我们知道了逻辑回归模型的假设分布是一个指数型分布, 然后我们再来看看广义线性模型。
2.2.2 广义线性模型
首先, 广义线性模型的代表:
- 逻辑回归(拟合的伯努利分布)
- 线性回归(拟合的高斯分布)
这个是不是又和前面对上了, 考虑一个分类或回归问题, 我们就是想预测某个随机变量y, y是某些特征x的函数, 为了推导广义线性模型, 我们必须做出如下三个假设:
- 第一条说的就是我们要拟合的这个随机变量y的分布, 并且是一个指数族分布, 而逻辑回归拟合的伯努利分布是不是正是这个?
- 第二条说的就是怎么去拟合这个分布,也就是拟合这个分布的哪些统计量能代表这个分布。这里拟合的就是这个分布的期望
- 第三条就是线性的含义, 为啥是广义线性, 这个地方指出来了
有了上面的理论, 下面就可以深层剖析LR里面的sigmoid:
LR是个二分类问题, 并且假设了样本服从伯努利分布, 即 p ( y ∣ x ; θ ) ∼ p(y \mid x ; \theta) \sim p(y∣x;θ)∼ Bernoulli ( ϕ ) (\phi) (ϕ), 那么:
h θ ( x ) = E [ y ∣ x ; θ ] = ϕ = 1 1 + e − η = 1 1 + e − θ T x \begin{aligned} h_{\theta}(x) &=E[y \mid x ; \theta] \\ &=\phi \\ &=\frac{1}{1+e^{-\eta}} \\ &=\frac{1}{1+e^{-\theta^{T} x}} \end{aligned} hθ(x)=E[y∣x;θ]=ϕ=1+e−η1=1+e−θTx1
因为根据指数族分布里面伯努利分布的那个推导公式
η = log Φ 1 − Φ ⇒ Φ = 1 1 + e − η \eta=\log \frac{\Phi}{1-\Phi} \Rightarrow \Phi=\frac{1}{1+e^{-\eta}} η=log1−ΦΦ⇒Φ=1+e−η1
而又根据广义线性模型的第三条:
η = θ T X \eta=\theta^{T} X η=θTX
所以最后就推出了sigmoid函数。 其实是这样出来的, 而前面讲的几率比, 对数几率回归等都是基于指数族分布, 广义线性模型的理论推导出来的。
说完了逻辑回归, 下面再来说说优化算法了。
3. 常用的优化算法
优化算法包括梯度法和牛顿法。
3.1 梯度法
梯度法比较简单, 更新公式也整理过多遍, 这里不再多解释。 这里重点依然是那个问题: 为何沿着梯度的方向下降就是最快的?
之前整理的时候, 白话太多, 导致知识点不连贯, 这里直接上重点:
当我们在某个要优化的函数, 这里设为f(x), 我们在x点处, 然后沿着方向v进行移动, 到达f(x+v), 看下面图:
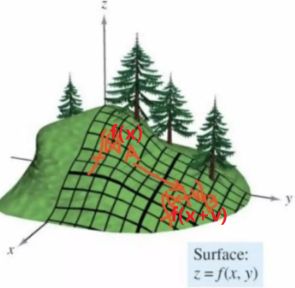
此图显示了从A点移动到B点的过程, 那么v方向是什么的时候, 局部下降的最快呢? 化成数学的语言就是, f ( x + v ) − f ( x ) f(x+v)-f(x) f(x+v)−f(x)的值在 v v v是什么的时候, 达到最大?
这里开始划重点: 泰勒公式
f ( x + Δ x ) ≈ f ( x ) + Δ x f ′ ( x ) + 1 2 Δ x 2 f ′ ′ ( x ) + O ( Δ x ) f(x+\Delta x) \approx f(x)+\Delta x f^{\prime}(x)+\frac{1}{2} \Delta x^{2} f^{\prime \prime}(x)+O(\Delta x) f(x+Δx)≈f(x)+Δxf′(x)+21Δx2f′′(x)+O(Δx)
下面我们对 f ( x + v ) f(x+v) f(x+v)在 v v v处进行Taylor一阶展开:
f ( x + v ) ≈ f ( x ) + ∇ f ( x ) T v f(x+v) \approx f(x)+\nabla f(x)^{T} v f(x+v)≈f(x)+∇f(x)Tv
进行化简得:
f ( x ) − f ( x + v ) ≈ − ∇ f ( x ) T v f(x)-f(x+v) \approx-\nabla f(x)^{T} v f(x)−f(x+v)≈−∇f(x)Tv
即 f ( x + v ) − f ( x ) = d f ( x ) ∗ v f(x+v)-f(x) = df(x)* v f(x+v)−f(x)=df(x)∗v, 则我们可以得出: d f ( x ) v d f(x) v df(x)v为函数值的变化量, 注意的是df(x)和v均为向量, d ( f x ) v d(fx) v d(fx)v, 也就是两个向量的点积, 而向量进行点积的最大值, 也就是两者共线的时候, 也就是说 v v v的方向和 d f ( x ) df(x) df(x)的方向相同的时候, 点积值最大, 这个点积值也代表了从A点到B点的上升量。
而 d f ( x ) df(x) df(x)正是代表函数值在x处的梯度, 前面又说明了 v v v的方向和 d f ( x ) df(x) df(x)的方向相同的时候, 点积值(变化值)最大, 所以说明了梯度方向是函数局部上升最快的方向。 也就证明了梯度的负方向是局部下降最快的方向。
3.2 牛顿法
关于牛顿法, 先摆结论, 然后给出证明, 更新公式长下面这个样子:
x t + 1 = x t − f ′ ( x t ) f ′ ′ ( x t ) x_{t+1}=x_{t}-\frac{f^{\prime}\left(x_{t}\right)}{f^{\prime \prime}\left(x_{t}\right)} xt+1=xt−f′′(xt)f′(xt)
也可以加入步长。 可以对比一下梯度下降法, 那个是只涉及到了一阶导数, 而这个加入了二阶导数。
下面是证明,依然是泰勒:
f ( x + Δ x ) ≈ f ( x ) + Δ x f ′ ( x ) + 1 2 Δ x 2 f ′ ′ ( x ) + O ( Δ x ) f ( x ) = f ( x 0 ) + ( x − x 0 ) f ′ ( x 0 ) + 1 2 ( x − x 0 ) 2 f ′ ′ ( x 0 ) + O ( … ) \begin{array}{l} f(x+\Delta x) \approx f(x)+\Delta x f^{\prime}(x)+\frac{1}{2} \Delta x^{2} f^{\prime \prime}(x)+O(\Delta x) \\ f(x)=f\left(x_{0}\right)+\left(x-x_{0}\right) f^{\prime}\left(x_{0}\right)+\frac{1}{2}\left(x-x_{0}\right)^{2} f^{\prime \prime}\left(x_{0}\right)+O(\ldots) \end{array} f(x+Δx)≈f(x)+Δxf′(x)+21Δx2f′′(x)+O(Δx)f(x)=f(x0)+(x−x0)f′(x0)+21(x−x0)2f′′(x0)+O(…)
我们把f(x)展开到二阶, 然后两边同时对x(变量)求梯度:
f ( x ) = f ( x 0 ) + ( x − x 0 ) f ′ ( x 0 ) + 1 2 ( x − x 0 ) 2 f ′ ′ ( x 0 ) + O ( … ) f ′ ( x ) = f ′ ( x 0 ) + ( x − x 0 ) f ′ ′ ( x 0 ) \begin{array}{c} f(x)=f\left(x_{0}\right)+\left(x-x_{0}\right) f^{\prime}\left(x_{0}\right)+\frac{1}{2}\left(x-x_{0}\right)^{2} f^{\prime \prime}\left(x_{0}\right)+O(\ldots) \\ f^{\prime}(x)=f^{\prime}\left(x_{0}\right)+\left(x-x_{0}\right) f^{\prime \prime}\left(x_{0}\right) \end{array} f(x)=f(x0)+(x−x0)f′(x0)+21(x−x0)2f′′(x0)+O(…)f′(x)=f′(x0)+(x−x0)f′′(x0)
这时候, 由于我们是在求极值, 令f’(x)=0, 就可得到结论:
x t + 1 = x t − f ′ ( x t ) f ′ ′ ( x t ) x_{t+1}=x_{t}-\frac{f^{\prime}\left(x_{t}\right)}{f^{\prime \prime}\left(x_{t}\right)} xt+1=xt−f′′(xt)f′(xt)
关于牛顿法, 计算太慢了, 所以目前用的比较少, 因为这些x可不是1个数, 这些都是向量, 并且二阶导这里是一个海塞矩阵, 而分母上的话就涉及到了矩阵求逆的问题了。 所以计算量太大了,并且也不一定逆矩阵存在。 所以更多的时候用的拟牛顿法。
最后, 再来看看正则。
4. 正则化
正则化的目的: 减小模型参数大小或者参数的数量, 缓解过拟合。 正则化其实就是在原来的目标函数的基础上又加了一项非负项, 并且这个非负项是 w w w的函数。 这样的话target不变的基础上得让这个loss变得小一点, 相当于对其产生了一种约束。 比如之前的时候, 我要拟合100, 我又10个 w w w, 假设特征是1, 那么这时候, 我每个 w w w要是10, 而如果后面加了个非负, 相当于我10个 w w w拟合的值不足100了, 那么要么去 w w w, 要么w都变得小一点。 这正好对应了L1和L2的方式。
正则化的通用形式:
Loss − with − regularization = loss ( w , x ) + λ f ( w ) \text { Loss }_{-} \text {with }_{-\text {regularization}}=\operatorname{loss}(w, x)+\lambda f(w) Loss −with −regularization=loss(w,x)+λf(w)
此处的 λ \lambda λ为正则化系数。关于正则化:
- 正则化恒为非负
- 正则化项又称为惩罚项, 惩罚的是模型的参数
- 正则化系数调节惩罚的力度, 越大则惩罚力度越大。
正则化的方法: L1正则和L2正则
-
L2正则化: 对参数进行二次约束
Loss − with − L 2 − regularization = loss ( w , x ) + λ ∥ W ∥ 2 2 \text { Loss }_{-} \text {with }_{-} L 2_{-} \text {regularization }=\operatorname{loss}(w, x)+\lambda\|W\|_{2}^{2} Loss −with −L2−regularization =loss(w,x)+λ∥W∥22
特性: 参数W变小, 但不为0, 不会形成稀疏解。 -
L1正则化:对参数进行一次约束, 会形成稀疏解
Loss − with − L 1 − regularization = loss ( w , x ) + λ ∣ W ∣ \text { Loss }_{-} \text {with }_{-} L 1_{-} \text {regularization }=\operatorname{loss}(w, x)+\lambda |W| Loss −with −L1−regularization =loss(w,x)+λ∣W∣
注意一点:无论L1、L2正则化方法, 本质上都是乘法参数w使其等于或者趋向于0, 但有没有可能有一种正则化方法会使其参数w趋向于非零值呢? 可以这样做。
Loss − with − X X − regularization = loss ( w , x ) + λ ∥ W − A ∥ 2 2 \text { Loss }_{-} \text {with }_{-} XX_{-} \text {regularization }=\operatorname{loss}(w, x)+\lambda\|W-A\|_{2}^{2} Loss −with −XX−regularization =loss(w,x)+λ∥W−A∥22
下面又是画重点, 即L1和L2分别形成稀疏和非稀疏解的原因。
第一个角度,就是图像的角度
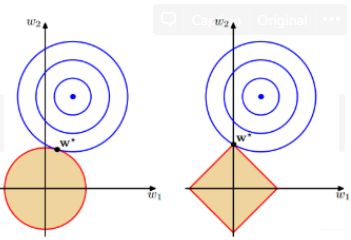
直观感受: 黄色区域表示正则项限制, 蓝色区域表示优化项的等高线, 要满足在两者交点上的点才符合最优解 w ∗ w* w∗, 故: 但 w w w的等高线逐步向正则限制条件区域扩散的时候, 前者交点大多在非坐标轴上, 后者在坐标轴上。关于这个的详细解释, 可以参考我整理的Pytorch正则化那部分。这里主要是整理一下第二个角度。
第二个角度, 求导。
从表达式上来看, L2和L1分别如上图表示, 我们想要求最小值, 很直观的一个方法就是求导, 那么不妨看看L1和L2正则化下的目标函数的导数。
- 如果我们看L2的导数, 如果想是极值点, 就是 L ′ + 2 λ w = 0 L'+2 \lambda w=0 L′+2λw=0, 这时候如果L2想产生稀疏解, 也就是 w w w等于0了, 那么 L ′ ( w ) L'(w) L′(w)就必须是0的时候, 才会产生稀疏的解。 但是 L ′ ( w ) L'(w) L′(w)是0的概率是很小的, 哪有那么巧的事情? 所以L2不太容易产生稀疏的解(当然不是不能)
- 再看L1的导数, 由于L1带有绝对值, 所以这个时候,得分开讨论。也就是下面这三种情况, 但
- w > 0 w>0 w>0的时候, 绝对值号可以直接去掉, L ′ + l a m b d a = 0 L'+lambda=0 L′+lambda=0, L ′ = − l a m b d a L'=-lambda L′=−lambda。
- w < 0 w< 0 w<0的时候, L ′ = l a m b d a L'=lambda L′=lambda,
这两种情况都不是稀疏解。但是这时候又是L’是个固定的值, 这种情况很少的。 所以不是稀疏解的可能性很小。 而要产生稀疏解的时候, 也就是 w = 0 w=0 w=0, 这时候是没有导数的, 只能拿一个次梯度来代替, 也就是 L ′ L' L′在上面那个范围里面, 这个是非常有可能的。 所以才容易稀疏解。
关于逻辑回归, 优化算法和正则化就先补充这么多,后面如果发现还有重要的, 会再进行补充。 上面这些点, 可以一些面试中常考的点。 关于更多逻辑回归的东西, 可以参考下面这篇文章。
【机器学习】逻辑回归(非常详细)- 阿泽哥这篇文章梳理的透透的了
逻辑回归是面试非常喜欢问的一个模型, 关于面试的重点, 可以参考下面这篇文章:
逻辑回归的常见面试点总结