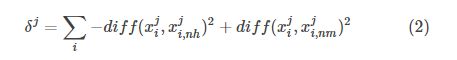【特征工程】特征选择方法
目录
1. 为什么要进行特征选择?
2. 特征选择与特征降维的区别
3. 特征选择方法:
2.1 过滤式选择
假设检验的内涵
假设检验的步骤
卡方检验和F检验的区别:
2.2 包裹式选择
2.3 嵌入法选择
4. 高级特征
详细参考内容在这里~
1. 为什么要进行特征选择?
- (降维)减轻维度灾难的问题
- 去除不相关的特征往往可以降低学习任务的难度
2. 特征选择与特征降维的区别
- 特征降维:
降维本质上是从一个维度空间映射到另一个维度空间,特征的多少并没有减少,当然在映射的过程中特征值也会相应的变化。举个例子,现在的特征是1000维,我们想要把它降到500维。降维的过程就是找个一个从1000维映射到500维的映射关系。原始数据中的1000个特征,每一个都对应着降维后的500维空间中的一个值。假设原始特征中有个特征的值是9,那么降维后对应的值可能是3。
特征选择
特征选择就是单纯地从提取到的所有特征中选择部分特征作为训练集特征,特征在选择前和选择后不改变值,但是选择后的特征维数肯定比选择前小,毕竟我们只选择了其中的一部分特征。举个例子,现在的特征是1000维,现在我们要从这1000个特征中选择500个,那个这500个特征的值就跟对应的原始特征中那500个特征值是完全一样的。对于另个500个没有被选择到的特征就直接抛弃了。假设原始特征中有个特征的值是9,那么特征选择选到这个特征后它的值还是9,并没有改变。
3. 特征选择方法:
2.1 过滤式选择
先对数据集进行特征选择,然后再训练学习器。 即特征选择过程与后续学习器无关。
(1) 方差筛选
- 单纯只从特征本身的角度来看
方差越大的特征,认为它比较有用;方差较小,那这个特征就不能提供什么信息。
比如,某个特征的方差为0,即所有的样本该特征的取值都是一样的,那么它对我们模型的训练将不会起到任何作用,可以将其舍弃。
实际应用中,我们可以指定一个方差阈值,方差小于该阈值的特征将被筛选掉。【sklearn中的VarianceThreshold类可以很方便的完成这个工作】
(2) 相关系数
- 主要用于输出连续值的监督学习算法中
分别计算所有训练集中各个特征与输出值之间的相关系数,设定一个阈值,选择相关系数较大的部分特征
from scipy.stats import pearsonr
```
# 计算特征与目标变量之间的相关度
# 1)输入:x为特征,y为目标变量.
# 2)输出:r: 相关系数 [-1,1]之间,p-value: p值。
# 注: p值越小,表示相关系数越显著,一般p值在500个样本以上时有较高的可靠性。
```
pearsonr(x,y) (3)假设检验
假设检验的内涵
H0 为原假设,H1为备择假设,两者互斥。
在假设检验中,由于随机性我们可能在决策上犯两类错误:
- 一类是假设正确,但我们拒绝了假设,这类错误是“弃真”错误,被称为第一类错误;(即选择H1,放弃H0)
- 一类是假设不正确,但我们没拒绝假设,这类错误是“取伪”错误,被称为第二类错误。(即选择H0,放弃H1)
一般来说,在样本确定的情况下,任何决策无法同时避免两类错误的发生,即在避免第一类错误发生机率的同时,会增大第二类错误发生的机率;或者在避免第二类错误发生机率的同时,会增大第一类错误发生的机率。人们往往根据需要选择对那类错误进行控制,以减少发生这类错误的机率。
大多数情况下,人们会控制第一类错误发生的概率。
发生第一类错误的概率被称作显著性水平,一般用α表示,在进行假设检验时,是通过事先给定显著性水平α的值而来控制第一类错误发生的概率。
如果将α = 0.05作为小概率事件的标准。
假设检验的步骤
1)、确定假设:假设抽样数据与总体没有显著差异性;
2)、进行抽样,得到一定的数据;
3)、根据假设条件下,构造检验统计量,并根据抽样得到的数据计算检验统计量在这次抽样中的具体值;
4)、依据所构造的检验统计量的抽样分布,和给定的显著性水平,确定拒绝域及其临界值;
5)、比较这次抽样中检验统计量的值与临界值的大小,如果检验统计量的值在拒绝域内,则拒绝假设
python数据分析之假设检验
- 卡方检验:检验某个特征分布与输出值分布之间的相关性
在sklearn中,可以使用chi2这个类来做卡方检验得到所有特征的卡方值与显著性水平P临界值,我们可以给定卡方值阈值, 选择卡方值较大的部分特征。
卡方检验的实现、卡方检验
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
model1 = SelectKBest(chi2, k=2)#选择k个最佳特征
#iris.data是特征数据,iris.target是标签数据,该函数可以选择出k个特征
model1.fit_transform(iris.data, iris.target)
model1.scores_ # 卡方检验的得分
model1.pvalues_ # p-values(p值)- F检验、T检验
它们都是使用假设检验的方法,只是使用的统计分布不是卡方分布,而是F分布和t分布而已。
在sklearn中,有F检验的函数f_classif和f_regression,分别在分类和回归特征选择时使用。
python levene检验、T检验、卡方检验、F检验
T检验与F检验的区别(通俗理解)
卡方检验和F检验的区别:
卡方检验是求出两个具有频数的数据组的一致性(针对类型数据);F检验是检验两组数值的差异的显著性(针对数值数据)。
前者只讨论事件出现的频数比如老鼠是否患癌;患癌记1,不患记0;
后者是计量型数值,比如癌肿重量。
- 互信息,即从信息熵的角度分析各个特征和输出值之间的关系评分。
在决策树算法中我们讲到过互信息(信息增益)。互信息值越大,说明该特征和输出值之间的相关性越大,越需要保留。
在sklearn中,可以使用mutual_info_classif(分类)和mutual_info_regression(回归)来计算各个输入特征和输出值之间的互信息。
★ 参考博主经验是:在没有什么思路的 时候,可以优先使用卡方检验和互信息来做特征选择
- Relief:详解
当一个属性对分类有利时,则该同类样本在该属性上的距离较近,而异类样本在该属性上的距离较远。
属性 j 对应的相关统计量为:
公式(2)得到的是单个样本对每个属性的评价值,将所有样本对同一个属性的评价值进行平均就得到了该属性的相关统计分量,分量值越大,分类能力就越强。
▶ 可以指定一个阈值 t,选择比 t 大的相关统计量分量所对应的特征
▶ 也可以指定选取的特征个数K,选择相关特征统计量分量最大的K个特征
2.2 包裹式选择
结合学习器一起考虑,直接把最终将要使用的学习器性能作为特征子集的评价准则。
>> 为给定的学习器选择最有利于其性能的特征子集。
- 最常用的包装法是递归消除特征法(recursive feature elimination,以下简称RFE)。
递归消除特征法使用一个机器学习模型来进行多轮训练,每轮训练后,消除若干权值系数的对应的特征,再基于新的特征集进行下一轮训练。
在sklearn中,可以使用RFE函数来选择特征。
>> 下面以经典的SVM-RFE算法来讨论这个特征选择的思路:
这个算法以支持向量机来做RFE的机器学习模型选择特征。它在第一轮训练的时候,会选择所有的特征来训练,得到了分类的超平面wx+b=0后,如果有n个特征,那么RFE-SVM会选择出w中分量的平方值w_i^2最小的那个序号i对应的特征,将其排除,在第二类的时候,特征数就剩下n-1个了,我们继续用这n-1个特征和输出值来训练SVM,同样的,去掉w_i^2最小的那个序号i对应的特征。以此类推,直到剩下的特征数满足我们的需求为止。
- 拉斯维加斯方法(LVW)
LVW 基于拉斯维加斯方法的框架,使用随机策略来进行子集搜索,以最终分类器的误差作为特征子集的评价标准。
假设数据集为 DD,特征集为 AA,则 LVW 每次从特征集 AA 中随机产生一个特征子集 A′A′,然后使用交叉验证的方法(伪代码的第 8 步)估计学习器在特征子集 A′A′ 上的误差,若该误差小于之前获得的最小误差,或者与之前的最小误差相当但 A′A′ 中包含的特征数更少,则将 A′A′ 保留下来。(《西瓜书》P251)
2.3 嵌入法选择
将特征选择过程与学习器训练过程融为一体,与包裹式选择在训练过程中边训练边筛掉特征不同,嵌入式选择是使用特征全集训练学习器,然后得到特征的重要性。
- 在sklearn中,使用SelectFromModel函数来选择特征。
- 此外也可以使用决策树或者GBDT。
那么是不是所有的机器学习方法都可以作为嵌入法的基学习器呢?也不是,一般来说,可以得到特征系数coef或者可以得到特征重要度(feature importances)的算法才可以做为嵌入法的基学习器。
4. 高级特征
我认为 也算是“冗余特征”,去除他们会减轻学习过程中的负担,但是,有时候冗余特征会降低学习任务的难度,相当于引入了一个学习的“中间概念”
寻找高级特征最常用的方法有:
若干项特征加和: 我们假设你希望根据每日销售额得到一周销售额的特征。你可以将最近的7天的销售额相加得到。
若干项特征之差: 假设你已经拥有每周销售额以及每月销售额两项特征,可以求一周前一月内的销售额。
若干项特征乘积: 假设你有商品价格和商品销量的特征,那么就可以得到销售额的特征。
若干项特征除商: 假设你有每个用户的销售额和购买的商品件数,那么就是得到该用户平均每件商品的销售额。
★ 参考博主的经验是,聚类的时候高级特征尽量少一点,分类回归的时候高级特征适度的多一点。