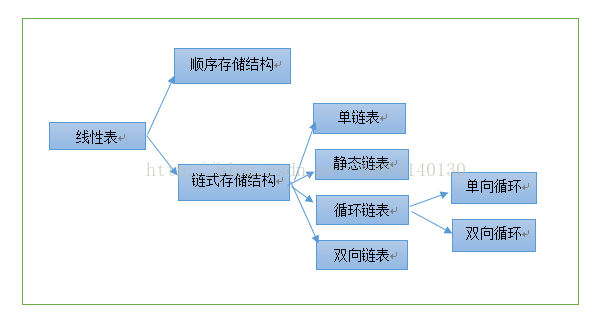
数据结构——线性表及线性表顺序存储

代码写的一定程度上，要再次提升的时候，是该好好的看一下数据结构和算法了。趁着最近有时间，好好的复习一下，今天主要是线性表和线性表的顺序存储。

线性表的概念

1、  线性表是一种最基本、最简单的的数据结构，是一种线性结构。

2、  线性表中数据元素之间的关系是一对一，是n个数据元素的有限序列。

3、  若将线性表记为(a1, ……, ai-1, ai,ai+1, ……,an),则表中ai-1领先于ai，ai领先于ai+1，称ai-1是ai的直接前驱元素，ai+1是ai的直接后继元素。当丨=1, 2, ……, n-1时，ai有且仅有一个直接后继，当i=2, 3, ……, n时，ai有且仅有一个直接前驱。

所以线性表元素的个数n (n>0)定义为线性表的长度，当n=0时，称为空表

线性表抽象数据类型定义如下

ADT 线性表 (List)

Data

Operation 

   void init(*L); //创建并初始化一个空线性表，如果成功返回true，修改表传指针  

   bool isEmpty(L); //判断一个线性表是否为空，不修改表传值  

   void clear(*L);        //清空一个线性表，成功返回true  

   bool get(L,i,*e);      //从某个位置取出元素并赋值给e(i的范围是[1,L.length])，修改e的值所以传递一个指针，成功返回true 

    location(L,e);       //查找线性表中是否有e，如果有返回它的位置(从1开始)，否则返回0表示失败 

   bool insert(*L,i,e);   //插入一个元素e在第i个元素之前(i的取值范围是[1,L.length+1]) ，成功返回true  

   bool delete(*L,i,*e);  //删除在第i个位置上的元素(i的取值范围是[1,L.length]),删除的元素赋给e，成功返回true 

   int size(L); //返回线性表的元素个数 

endADT

线性表的顺序存储结构

线性表的顺序存储结构是最简单最常用的数据结构，用一段连续地址依次存储表中的数据元素。下面我们用代码来实现：

#include
#include
#include


typedef int ElemType;

typedef struct{
	ElemType data[20];//存储空间初始容量20
	int length;
} Arr;
int initArr(Arr *a){
	a->length = 0;
	return 1;
}
//创建顺序表
Arr create(Arr a){
	int i;
		for (i = 0; i < 10; i++){
		a.data[i] = rand() % 100;//随机模拟顺序表元素
		a.length++;
	}
	return a;
}
//打印所有元素
int print(Arr a){
	int i;
	for (i = 0; i < a.length; i++){
		printf("%d,", a.data[i]);
	}
	printf("\n");
	return 1;
}
//插入元素
int insert(Arr* a, int pos, ElemType ele){
	int k;
	if (a->length == 20){//顺序线性表已满
		return 0;
	}
	if (pos<1 || pos>a->length + 1){//插入位置不合法
		return 0;
	}
	if (pos <= a->length){//中间插入
		for (k = a->length; k > pos - 1; k--){//注意下标=pos-1
			a->data[k + 1] = a->data[k];//将要插入位置之后的元素向后移动一位
		}
	}
	a->data[pos - 1] = ele;//插入新元素
	a->length++;
	printf("插入元素成功,插入位置%d,插入元素%d\n", pos, ele);
	return 1;
}
//判断是否为空
int isEmpty(Arr a){
	if (a.length == 0){
		printf("长度为0");
		return 1;
	}
	else{
		printf("长度不为0");
		return 0;
	}
}
//清空表
int clear(Arr *a){
	a->length = 0;
	return 1;
}
//返回表的大小
int size(Arr a){
	return a.length;
}
//查找指定位置元素
int get(Arr a, int pos ,ElemType * e){
	if (a.length = 0 || pos<1 || pos>a.length){
		printf("查找位置不合法\n");
		return 0;
	}
	*e = a.data[pos - 1];
	printf("查找位置%d元素为%d\n",pos,*e);
	return 1;
}
//删除指定位置元素
int deleteEle(Arr *a, int pos,ElemType *e){
	int k;
	if (a->length == 0){
		printf("删除位置不合法\n");
		return 0;
	}
	if (pos<1 || pos>a->length){
		printf("删除位置不合法\n");
		return 0;
	}
	*e = a->data[pos - 1];
	if (pos < a->length-1){
		for (k = pos; k < a->length; k++){
			a->data[k - 1] = a->data[k];
		}
	}
	printf("删除成功,删除元素%d\n",*e);
	a->length--;
	return 1;
}

int main(){
	Arr a;
	ElemType e;
	int i = initArr(&a);
	printf("初始化A,初始长度为：%d\n", a.length);
	a = create(a);
	printf("创建顺序队列A,长度为：%d\n", a.length);
	print(a);
	insert(&a, 3, 5);
	print(a);
	get(a, 2,&e);
	
	deleteEle(&a, 2,&e);
	
	print(a);

	system("pause");
}

运行结果如下：

线性表顺序存储的时间复杂度：

1、最好的情况，如果元素要插入到最后一个位置，或者删除最后一个元素， 此时时间复杂度为0(1)，因为不需要移动元素的。

2、最坏的情况，如果元素要插入到第一个位置或者删除第一个元素，那就意味着要移动所有的元素向后或者向前，函数要对线性表循环一遍操作，所以这个时间复杂度为 0(n)。

3、平均的情况，由于元素插入到第i个位置，或删除第i个元素，需要移动n—i个元素。根据概率原理，每个位置插入或删除元素的可能性是相同的，也就说位置靠前，移动元素多，位置靠后，移动元素少。最终平均移动次数和最中间的那个元素的移动次数相等，为(n-1)/2。因此时间复杂度为0(n)。

 

线性表顺序存储的优缺点：

优点：查询速度快，简单、运算方便，更适合小线性表或者固定长度的线性表。

缺点：删除和插入效率较低；存储空间容易出现上溢；容易出现空间浪费。