2020届顺丰科技视觉算法工程师提前批面经

7.30号下午三点到三点半面试的，视频面试，牛客网的平台还比较正规，但是面试时跟之前看到的面经说的有点出入，不只是问项目，还问了些基础，但也会围绕简历内容展开，感觉自己还是欠缺很多知识

主要内容：

1，讲一个你熟悉的项目，用了哪些算法，说说你自己的理解
2，解释一下SSD与Fast RCNN 本质上的区别
3，知道哪些激活函数，这里往深了问，比如sigmod的问题在哪里，relu是怎么解决的，relu的问题在哪里，有没有对应的解决算法（prelu），其实这些平时都看到过，结果这次说得吞吞吐吐，也记不清楚了
4，BN层的定义以及功能，后面说了最好是能写出公式来，我说得不是很对，但面试官说一般也只是用，没关系
5，yolov3是否有池化层，我说记得好像是没有，然后回想了一下，面试官就解释图像缩小尺寸除了使用池化层还可以在padding上操作，卷积核只要不是1x1都能是尺寸变小，幸好说了记得没有，不然连yolov3的框架都不了解就太水了
6，最后问我有什么想问的，说了一会儿之后问Kmeans的K在算法里是怎么放置的，他问是一下全取出来还是一个一个取，我说是随机取出k个来吧，他说这就能看出来你基础不牢，这里有点晕

面试官还是很好，也没有太怼我什么，问问题也是引导性的，感觉自己真的没准备好，基础知识也不牢固，面试过程很快，十来分钟说技术，然后就是问他一些东西

总结一下这些问题的解决办法：

一、SSD与Fast RCNN 本质上的区别

自己没有总结太清楚，面试官是这么解释的：主要是anchor机制不同，SSD的anchor机制是在多个feature map上应用，这样可以利用多层的特征并且自然的达到多尺度的检测；而Fast RCNN 通过CNN得到候选框，anchor是应用在全连接层做检测（面试官是这么说的，也没有百度到比较准确的答案）

二、激活函数

一般的激活函数就sigmoid、relu、tanh
sigmoid函数图":

该函数是将取值为 (−∞,+∞) 的数映射到 (0,1) 之间
缺点：当 z 值非常大或者非常小时，通过上图我们可以看到，sigmoid函数的导数 g′(z) 将接近 0 。这会导致权重 W 的梯度将接近 0 ，使得梯度更新十分缓慢，即梯度消失。

tanh函数
  tanh函数相较于sigmoid函数要常见一些，该函数是将取值为 (−∞,+∞) 的数映射到 (−1,1) 之间，其公式与图形为：
  
  tanh函数在 0 附近很短一段区域内可看做线性的。由于tanh函数均值为 0 ，因此弥补了sigmoid函数均值为 0.5 的缺点。
缺点：tanh函数的缺点同sigmoid函数的缺点一样，当 z 很大或很小时，g′(z) 接近于 0 ，会导致梯度很小，权重更新非常缓慢，即梯度消失问题。

ReLU函数
ReLU函数又称为修正线性单元（Rectified Linear Unit），是一种分段线性函数，其弥补了sigmoid函数以及tanh函数的梯度消失问题。

对于ReLU函数的求导为：
g′(z)={1,if z>0
0 if z<0
ReLU函数的缺点：当输入为负时，梯度为0，会产生梯度消失问题。同时也能保证模型的稀疏性

面试官问: 这里针对Relu的缺点对应的改进？
Leaky Relu ：这是一种对ReLU函数改进的函数，又称为PReLU函数，但其并不常用。其公式与图形如下：
g(z)={z,if z>0
az,if z<0

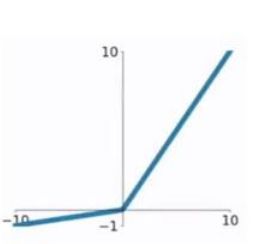
其中 a 取值在 (0,1) 之间。
Leaky ReLU函数的导数为：
g(z)={1,if z>0
a,if z<0
Leaky ReLU函数解决了ReLU函数在输入为负的情况下产生的梯度消失问题

三、BN层的定义以及功能

参考回答：

神经网络在训练的时候随着网络层数的加深,激活函数的输入值的整体分布逐渐往激活函数的取值区间上下限靠近(求导为0),从而导致在反向传播时低层的神经网络的梯度消失。而BatchNormalization的作用是通过规范化的手段,将越来越偏的分布拉回到标准化的分布,将输出信号x规范化到均值为0，方差为1保证网络的稳定性使得激活函数的输入值落在激活函数对输入比较敏感的区域,从而使梯度变大,加快学习收敛速度,避免梯度消失的问题（我也是说解决梯度消失的问题，但是面试官说BN并不是为了解决梯度消失的问题，不觉明历，可能又发现新的可以解决问题了）

四、K-means

我当时说的是随机选择k个数据作为类心，结果被面试官说基础没掌握好，有点蒙，后来去查了，还有个Kmeans++算法，跟他说的初始化类心方法接近。

kmeans其算法思想大致为：事先确定常数K，常数K意味着最终的聚类类别数，首先随机选定初始点为质心，并通过计算每一个样本与质心之间的相似度(这里为欧式距离)，将样本点归到最相似的类中，接着，重新计算每个类的质心(即为类中心)，重复这样的过程，直到质心不再改变，最终就确定了每个样本所属的类别以及每个类的质心。由于每次都要计算所有的样本与每一个质心之间的相似度，故在大规模的数据集上，K-Means算法的收敛速度比较慢。
  根据以上描述，我们大致可以猜测到实现kmeans算法的主要三点：
  （1）簇个数 k 的选择
  （2）各个样本点到“簇中心”的距离
  （3）根据新划分的簇，更新“簇中心”
对每一类中的数据初步选取类心，取的方式有多种如：
1.该类所有数据的均值；
2.随机取k个数据作为类心；
3.选取距离最远的k个点作为类心等。
（这里也没有初始类心得一个一个放的意思，面试官问的是kmeans，那我确实没有说错）

k-means++是k-means的变形，通过小心选择初始簇心，来获得较快的收敛速度以及聚类结果的质量

k-means++是先随机选择一个数据项作为第一个初始的簇心，根据这1个簇心，我们通过一系列计算，获得第2个簇心，再根据这2个簇心，通过计算获得第3个簇心。。。以此类推，最终，获得全部的k个簇心，然后，再按照上面k-means的做法，做聚类分析。

类心选取算法描述如下：

步骤一：随机选取一个样本作为第一个聚类中心 c1；
步骤二：计算每个样本与当前已有类聚中心最短距离（即与最近一个聚类中心的距离），用 D(x)表示；
这个值越大，表示被选取作为聚类中心的概率较大；
最后，用轮盘法选出下一个聚类中心；
步骤三：重复步骤二，知道选出 k 个聚类中心。