快速排序

特性：

时间复杂度O(n^2)

归并排序和快速排序都采用了分治算法 

-、基础实现

//————————————————————快速排序——————————————---—/
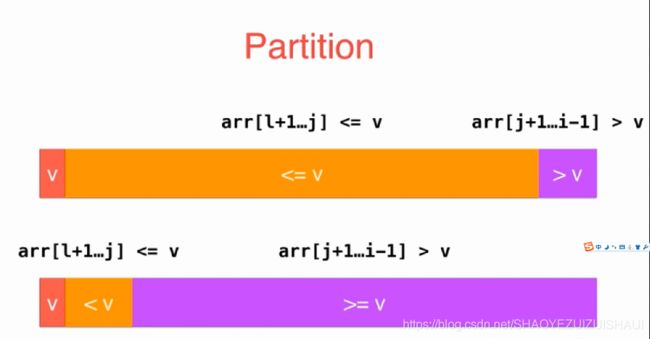
//对arr[L...R]部分进行parttition操作
//返回给p，使得arr[L,...p-1]arr[p]
template 
int __partition(T arr[], int L,int R)
{
	
	int j = L;
	for (int i = L+1; i <= R; i++)
	{
		if (arr[L] > arr[i])
		{
			swap(arr[i], arr[++j]);

		}
	}
	swap(arr[L], arr[j]);
	return j;
}
template 
//对arr[l...r]部分进行快速排序
void _quickSort(T arr[],int L,int R)
{
	if (L >= R)
		return;
	int p = __partition(arr, L, R);
	_quickSort(arr,L, p-1);
	_quickSort(arr, p+1, R);
}
template 
void quickSort(T arr[], int n)
{
	_quickSort(arr, 0,n-1);
}

基础算法在近乎有序或者完全有序情况下，出现最差情况！

加入随机种子：让快速排序在近乎有序的数列中，不至于每次都是最小的元素，是的两边数列数量分布严重不平衡

//————————————————————快速排序——————————————---—/
//对arr[L...R]部分进行parttition操作
//返回给p，使得arr[L,...p-1]arr[p]
template 
int __partition(T arr[], int L,int R)
{
	swap(arr[L], arr[rand() % (R - L + 1) + L]);
	int j = L;
	for (int i = L+1; i <= R; i++)
	{
		if (arr[L] > arr[i])
		{
			swap(arr[i], arr[++j]);

		}
	}
	swap(arr[L], arr[j]);
	return j;
}
template 
//对arr[l...r]部分进行快速排序
void _quickSort(T arr[],int L,int R)
{
	if (L >= R)
		return;
	int p = __partition(arr, L, R);
	_quickSort(arr,L, p-1);
	_quickSort(arr, p+1, R);
}
template 
void quickSort(T arr[], int n)
{
	srand(time(NULL));
	_quickSort(arr, 0,n-1);
}

当有大量重复值存在时，又会出现左右分布不平衡，导致近乎O(n^2)

template 
int __partition2(T arr[], int L, int R)
{
	swap(arr[L], arr[rand() % (R - L + 1) + L]);
	int i=L+1, j=R;
	//一定要保证，最后交换的值是处于小于arr[L]状态
	while (i <= R && i<=j)
	{

		if (arr[i] >= arr[L])
		{
			while (j >= L+1 && i <= j)
			{
				if (arr[j] <= arr[L])
				{
					swap(arr[i], arr[j]);
					j--;
					break;
				}
				j--;	
			}		
			
		}
	
		i++;

	}
	swap(arr[L], arr[j]);
	return j;
}

template 
//对arr[l...r]部分进行快速排序
void _quickSort(T arr[],int L,int R)
{
	if (L >= R)
		return;
	int p = __partition2(arr, L, R);
	_quickSort(arr,L, p-1);
	_quickSort(arr, p+1, R);
}
template 
void quickSort(T arr[], int n)
{
	srand(time(NULL));
	_quickSort(arr, 0,n-1);
}

或者，像下面的思想，两种不一样的思想

template 
int __partition2_1(T arr[], int L, int R)
{
	swap(arr[L], arr[rand() % (R - L + 1) + L]);
	int i = L + 1, j = R;
	//一定要保证，最后交换的值是处于小于arr[L]状态
	while (true)
	{
		while (i <= R && arr[i] < arr[L])i++;
		while (j >= L + 1 && arr[j] > arr[L])j--;
		if (i > j) 
			break;
		swap(arr[i], arr[j]);
		i++;
		j--;
	}
	swap(arr[L], arr[j]);
	return j;
}
template 
//对arr[l...r]部分进行快速排序
void _quickSort(T arr[],int L,int R)
{
	if (L >= R)
		return;
	int p = __partition2_1(arr, L, R);
	_quickSort(arr,L, p-1);
	_quickSort(arr, p+1, R);
}
template 
void quickSort(T arr[], int n)
{
	srand(time(NULL));
	_quickSort(arr, 0,n-1);
}

还有一种方法：

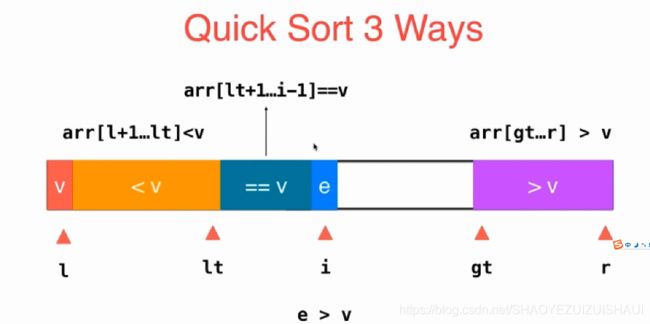
//_quickSort 分成三部分的优化方法
template 
//对arr[l...r]部分进行快速排序
void _quickSort(T arr[],int L,int R)
{
	if (L >= R)
		return;
	swap(arr[L], arr[rand() % (R - L + 1) + L]);
	//arr[L+1...LT]<[L]   arr[LT+1...i)==a[L] arr[j,R]>a[L]
	int i = L + 1, j = R + 1, LT = L;
	//一定要保证，最后交换的值是处于小于arr[L]状态
	while (i < j)
	{
		if (arr[i] < arr[L])
		{
			swap(arr[i], arr[++LT]);
			i++;
		}
		else if (arr[i] == arr[L])
		{
			i++;
		}
		else
		{
			swap(arr[i], arr[--j]);
		}
	}
	swap(arr[L], arr[LT]);
	_quickSort(arr,L, LT-1);
	_quickSort(arr, j, R);
}
template 
void quickSort(T arr[], int n)
{
	srand(time(NULL));
	_quickSort(arr, 0,n-1);
}