【运筹学】线性规划 单纯形法 ( 原理 | 约定符号 | 目标系数矩阵 C | 目标函数变量矩阵 X | 约束方程常数矩阵 b | 系数矩阵 A | 向量 | 向量符号 | 向量 Pj )

I . 单纯形法 引入

---

1. 方程组的解个数 :

• ① 唯一解 : 如果方程组的方程个数 等于 变量的个数 , 变量的解是唯一的 ;
• ② 多个解 : 如果方程组的方程个数 大于 变量的个数 , 变量的解可能会出现多个 ;

2. 单纯形法引入 : 在线性规划中 , 约束方程个数 , 一般情况下会小于变量个数 , 因此会有多个解 , 单纯形法就是针对这种情况求解的方法 , 可以得到符合要求的线性规划的最优解 ;

II . 单纯形法 基本原理

---

单纯形法原理 :

• ① 初始单纯形 : 先从线性规划 约束方程 中找出单纯形 , 每个单纯形可以解出一组变量的解 ;
• ② 判定趋势 ( 是否最优 ) : 然后判断这个解 影响的 目标函数的趋势 , 使目标函数增大 还是 减小 ;
• ③ 找到更优可行解 : 根据该趋势选择下一个单纯形 , 不断迭代 , 直到找到一个单纯形 , 使目标函数达到最大值或最小值 ;

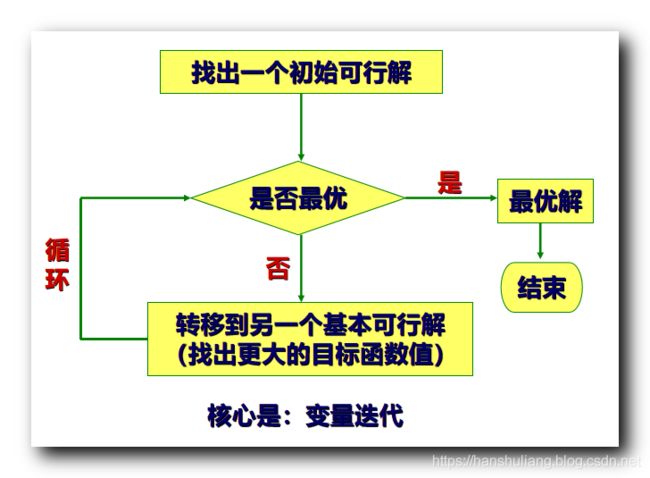
单纯形法 执行方案 :

• ① 初始可行解 : 先找到 一个 初始可行解 , 判定其是否是最优解 , 如果是到此为止结束 ;
• ② 判定 : 是否最优解 , 如果是 , 到此结束 ; 如果不是 , 继续执行 ③ ;
• ③ 转化更优的可行解 : 那么按照一定法则 , 转换成另一组优化后的 可行解 , 跳转到 ② 继续判定 ;

III . 线性规划 标准形式

---

线性规划标准形式 : 使用单纯形法 求解 线性规划问题 , 这里要求线性规划数学模型必须是标准形式 , 有如下要求 :

• ① 目标函数 : 变量组成的目标函数 , 求解极大值 ;
• ② 约束方程 : 所有的约束方程都必须是等式 , 并且右侧的常数都必须 大于等于 0 ;
• ③ 变量约束 : 所有的变量取值都必须大于等于 0 ;

线性规划标准形式转换方式 : 【运筹学】线性规划数学模型标准形式 ( 标准形式 | 目标函数转化 | 决策变量转化 | 约束方程转化 | 固定转化顺序 | 标准形式转化实例 ) , 参考上一篇博客内容 ;

IV . 线性规划 标准形式 普通形式公式

---

线性规划标准形式公式 : $n$ 个变量 , $m$ 个约束方程 , $n>m$ 变量数大于方程数 , 解有多个 ;

$$\begin{array}{l}maxZ={\sum }_{j=1}^n{c}_j{x}_j\\ \\ s.t\{\begin{array}{ll}{\sum }_{j=1}^n{a}_{ij}{x}_j=b_i& i=1,2,\cdots ,m\\ & \\ x_j\ge 0& j=1,2,\cdots ,n\\ & \\ b_i\ge 0& i=1,2,\cdots ,m\end{array}\end{array}$$

V . 线性规划 标准形式 展开完整形式公式

---

线性规划标准形式 展开式 : $n$ 个变量 , $m$ 个约束方程 , $n>m$ 变量数大于方程数 , 解有多个 ;

$$\begin{array}{l}maxZ=c_1{x}_1+c_2{x}_2+\cdots +c_n{x}_n\\ \\ s.t\{\begin{array}{l}{a}_{11}{x}_1+a_{12}{x}_2+\cdots +a_{1n}{x}_n=b_1\\ \\ a_{21}{x}_1+a_{22}{x}_2+\cdots +a_{2n}{x}_n=b_2\\ \\ \cdots \cdots \cdots \\ \\ a_{m1}{x}_1+a_{m2}{x}_2+\cdots +a_{mn}{x}_n=b_m\\ \\ x_1,x_2,\cdots ,x_n\ge 0\\ \\ b_1,b_2,\cdots ,b_n\ge 0\end{array}\end{array}$$

VI . 线性规划 标准形式 矩阵形式公式 ( 矩阵 C | 矩阵 X | 矩阵 b | 矩阵 A )

---

1. 线性规划标准形式 矩阵形式 : $n$ 个变量 , $m$ 个约束方程 , $n>m$ 变量数大于方程数 , 解有多个 ;

$$\begin{array}{l}maxZ=CX\\ \\ AX=b,X\ge 0\end{array}$$

2. 矩阵 $C$ : 该矩阵是行向量 , 代表了目标函数中的系数 ;
$$C=\left[\begin{array}{cccccc}& c_1,& c_2,& \cdots ,& c_m& \end{array}\right]$$*

3. 矩阵 $X$ : 该矩阵是列向量 , 表示目标函数中的变量 ;

$$\begin{gathered} X=\left[\begin{array}{c} \\ \\ x_1\\ \\ x_2\\ \\ ⋮\\ \\ x_m\\ \end{array}\right] \end{gathered}$$

4. 矩阵 $b$ : 该矩阵是列向量 , 表示约束方程的右侧常数 ;

$$\begin{gathered} b=\left[\begin{array}{c} \\ \\ b_1\\ \\ b_2\\ \\ ⋮\\ \\ b_m\\ \end{array}\right] \end{gathered}$$

5. 矩阵 $A$ : 该矩阵是 $m\times n$ 矩阵 , 有 $m$ 行 $n$ 列 , $m$ 表示约束方程个数 , $n$ 表示变量个数 ; ( $n>m$ )

$m$ 同时也是 矩阵 $A$ 的秩 ; 该矩阵是 $m$ 个 约束方程的每个变量前的 系数 矩阵 ;

$$\begin{gathered} A=\left[\begin{array}{cccccc} \\ & & & & & \\ & a_{11}& a_{12}& \cdots & a_{1n}& \\ & & & & & \\ & a_{21}& a_{22}& \cdots & a_{2n}& \\ & & & & & \\ & ⋮& ⋮& \ddots & ⋮& \\ & & & & & \\ & a_{m1}& a_{m2}& \cdots & a_{mn}& \\ & & & & & \end{array}\right] \end{gathered}$$

VII . 线性规划 标准形式 向量形式公式 ( 向量 Pj )

---

1. 向量概念 : 向量是特殊的矩阵 , $m$ 行 $1$ 列的矩阵 , 就是向量 ;

2. 线性规划 向量形式 : 其中 矩阵 $C$ , 矩阵 $X$ , 矩阵 $b$ 与上面的矩阵形式内容一致 , 本公式之比上个公式多了一个 向量 $P_j$ ;

$$\begin{array}{l}maxZ=CX\\ \\ s.t\{\begin{array}{l}{\sum }_{j=1}^n{P}_j{x}_j=b\\ \\ X\ge 0\end{array}\end{array}$$

3. 向量 $P_j$ 表示 : 该向量是 $m$ 行 $1$ 列的矩阵 , 表示 约束方程 $A$ 中的第 $j$ 行的列向量 , 其中 $j=1,2,\cdots ,n$ ;

$$\begin{gathered} P_j=\left[\begin{array}{c} \\ \\ a_{1j}\\ \\ a_{2j}\\ \\ ⋮\\ \\ a_{mj}\\ \end{array}\right] \end{gathered}$$

4. 矩阵 $A$ 与 向量$P_j$ 关系 :

$$\begin{gathered} A=\left[\begin{array}{cccccc} \\ & & & & & \\ & a_{11}& a_{12}& \cdots & a_{1n}& \\ & & & & & \\ & a_{21}& a_{22}& \cdots & a_{2n}& \\ & & & & & \\ & ⋮& ⋮& \ddots & ⋮& \\ & & & & & \\ & a_{m1}& a_{m2}& \cdots & a_{mn}& \\ & & & & & \end{array}\right]=\left[\begin{array}{cccccc}& P_1& P_2& \cdots & P_n& \end{array}\right] \end{gathered}$$

5. 系数替换方案 : 在线性规划 普通公式中 , 约束方程系数 $a_{ij}$ 可以使用 $P_j$ 进行替换 ;

$$\begin{gathered} \sum _{j=1}^n{a}_{ij}{x}_j=b_i \\ i=1,2,\cdots ,m \\ j=1,2,\cdots ,n \end{gathered}$$

向量 $P_j$ 代替其中的 $a_{ij}$ , 替换完毕后为 :
$$\begin{gathered} \sum _{j=1}^n{P}_j{x}_j=b_i \\ j=1,2,\cdots ,n \end{gathered}$$