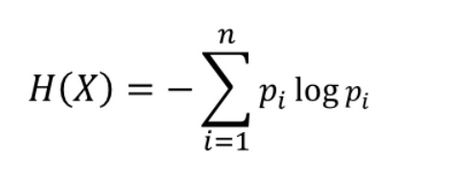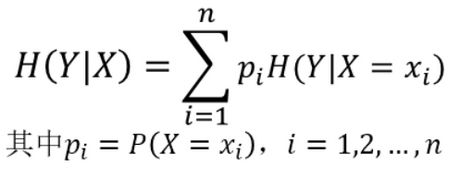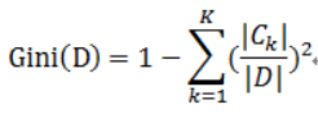谈分类之逻辑回归与决策树 ————算法及应用（类论与python实战）

文章综述：

对分类算法中的逻辑回归算法与决策树算法进行初步的了解，并使用Python语言分别生成数据使用两种算法进行分类。

逻辑回归只研究了二分类问题，通过代码实现发现，当数据分布较为规律，数据点类别的区分比较明显时，决策边界可以比较准确的找到，但是如果数据的分布比较杂乱，只使用二分类的逻辑回归效果很差，这一点从使用代码一定范围内随机生成数据在使用逻辑回归进行分类时可以发现，如果是多分类问题，逻辑回归还需要寻找适合的决策边界模型，而且只是二分类以w0+w1x1+w2x2为决策边界很多时候也很不合适。但是逻辑回归可以比较轻松的随时导入大量数据集对模型进行训练更新，对数据快速的进行分类，而且还可以随时调整分类的阈值。

      对于决策树回归只研究了ID3算法和ID4.5算法,CART算法的离散属性搭建树问题，对剪枝问题也没有过多的描述。采用了整段描述的形式逐步推出三种算法，分析其优劣点，并使用python对三种算法中最优的CART算法生成了一个数据集，根据数据集的多个特征进行了分类，并将决策树画出。在实现的过程中发现，决策树的实现相对来说没有复杂的算法，实现比较简单，而且轻松的实现了多个特征的多维分类，图形也非常形象易于理解，不过在生成决策树的时候非常容易过拟合，产生大量的叶子节点，需要通过剪枝去除，另外也无法像逻辑回归一样根据新的数据更新和优化模型。

算法学习：

逻辑回归（Logistic回归）：

逻辑回归是分类算法里最基础也是最重要的算法之一，而说到逻辑回归很多人就会想起刚刚学过的线性回归，那逻辑回归和线性回归有什么关系和区别呢？实际上逻辑回归和线性回归在形式上基本是相同的，都是利用回归的思想去解决问题，它们最大的区别就是因变量不同，在说明这一点之前我们首先要明确两者在用途上的差别，逻辑分类是一种分类算法，主要用来解决二分类或者多分类问题，而线性回归是对数据变量进行拟合，对未知变量进行估计预测。它们两个都有ax+b，但是在处理数据时线性回归将ax+b当成因变量使用y=ax+b来求值，而逻辑分类是将ax+b的值映射到[0,1]的范围之内，并将其分为大于0.5和小于0.5两类（这里用二分类线性决策边界解释），由此将数据集分成两类。

      了解过什么是逻辑分类后我们来进入主题正式讨论一下逻辑回归，逻辑回归就是找到一个界，这个界将数据分成两类，划分最准确，错误最少的那个界就是逻辑回归的最优的界。而现在有一个核心问题就是：我们如何找到这个界？这里我们讨论二分类所以我们设这个界为Z=XW=W0+W1X1+W2X2，也被称为决策边界，如图：

然后我们使用Sigmoid函数将其值映射到[0,1]之间，获得逻辑回归的决策函数h=1/1+e**-z，之所以选择用Sigmoid函数一是Sigmoid函数符合要求以0.5做分界，数学特性好。二是逻辑回归写成指数族分布的形式可以推导出sigmoid函数的形式。（具体原因可以阅读文献一）Sigmoid函数如图：

横坐标为z，z>0，概率h>0.5，概率最终趋于1..

z<0，概率h>0.5,概率最终趋于0.

在决策边界上是z=0，概率h=0.5.

当h>0.5的数据点我们将它归为一类，并给他们一个标签y=1.

当h<0.5的数据点我们将它归为另外一类，并给他们一个标签y=0.

而求最优决策边界就是对于边界方程式Z=XW=W0+W1X1+W2X2 通过已知的测试数据集（已被分好类拥有y标签并有X1,X2两个特征的数据），求出最优的三个未知量W0,W1,W2使决策边界可以对未知的有X1,X2两个特征的数据集进行划分，将其分为h>0.5,y=1的·一类与h<0.5,y=0的一类。在划分的过程中出现划分错误越少，决策边界越好。而这一标准我们可以用两个cost函数（代价函数）来描述：

label=1时，如图： cost=-log(h)

当y=1时，h>0.5趋近于1，所以图中当h越大时越接近1时cost越小，决策边界选取的越好。

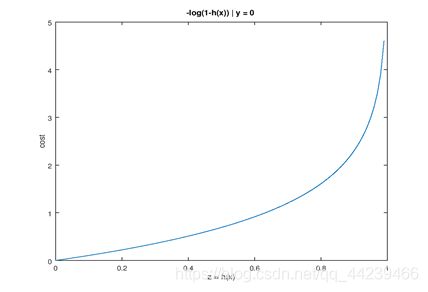
label=2时，如图:  cost=-log(1-h)

当y=0时，h<0.5趋近于0，所以图中当h越小时越接近0时cost越小，决策边界选取的越好。

   我们把两个cost函数总结在一起变成一个方程式为：cost=-ylog(h)-(1-y)log(1-h)。当cost最小时，选取的决策边界最优及W0,W1,W2选取的最优。自此求最优决策边界问题转化为求最小cost的问题。求最小cost，首先我们求出cost的导数:dcost/dw。求解如下:

      z=xw（x与w是矩阵相乘,z为多维数据，随着测试数据集的维度变化为（n,1））

      h=1/1+e**-z

      h=1/1+e**-xw

      cost=-ylog(h)-(1-y)log(1-h)

h对z求导为: -e**-z*-1/(1+e**-z)**z=1+e**-z-1/(1+e**-z)**2=1/1+e**-z(1-(1/1+e**-z))=h(1-h)

其中cost~h~z~wx

dcost/dw=(dc/dh)*(dh/dz)*(dz/dw)=X的转置*{（（-y/h）-(1-y/1-h)*-1）*h(1-h)}=X的转置*{（（-y(1-h)+h(1-y)/h(1-h)）*h(1-h)）}=X的转置*{(-y+y*h+h-h*y)}=X的转置*(h-y)

得到dcost/dw的值为: X的转置*((1/1+e**-xw)-y)

在得到梯度后我们便可以用梯度下降法来求最优的W（二分类维度为(3,1)）。

如图：当我们通过梯度下降法将w迭代到最低点时，梯度最小，cost最小，可以得到最优W。

过程如下：

1. 初始化w（这里我们选取初始值Wi）
2. 找到梯度dcost/dw= X的转置*((1/1+e**-xw)-y)
3. 梯度下降的公式w=w-alpha*(dc/dw)

(1.alpha为步长通常选取0.001、0.003、0.01、0.03等，不可选取过大，若选取过大可能导致无法收敛到最低点。2.这里取dc/dw为标量无方向可以使公式在最低点左右两侧均成立)

    4.反复迭代一定次数或一定阈值（随数据集的训练而优化）

解释：即初始化一个参数w，找到对应梯度，用此w乘以步长alpha，以此更新w，随着迭代次数变多，w越来越靠近最低点，dcost/dw的值会渐渐变小，直到迭代中w趋近于不变时便可得到最优w，其中步长的选取对迭代会有影响，可通过计算优化步长的选取参考文献二。

借助Python实现逻辑回归：

1. 生成数据集

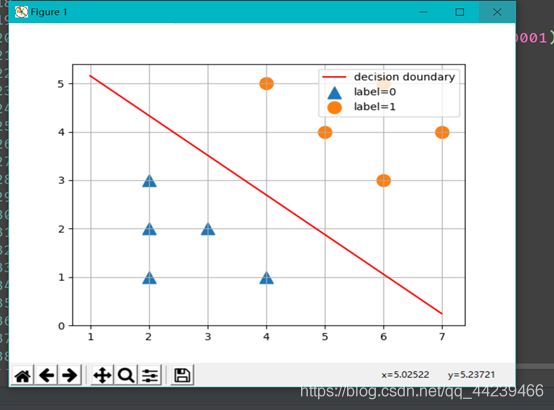
     2.导入数据集对求最优w迭代10000次，用并用图表显示：

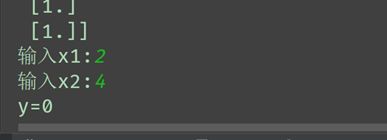
3.利用求出的w对输入数据分类：

代码演示

#引入库
import numpy as np
import matplotlib.pyplot as plt

#获取数据集
def getdata(filename):
    file = open(filename)
    x=[]
    y=[]
    for line in file.readlines():
        line=line.strip().split()
        x.append([1.0,float(line[0]),float(line[1])])
        y.append([float(line[2])])
    x_mat=np.mat(x)
    y_mat=np.mat(y)
    file.close()
    return x_mat,y_mat

#w的计算
def w_calc(x_mat,y_mat,alpha=0.001,iternumber=10001):
    #w的初始化
    w=np.mat(np.random.randn(3,1))
    #w的迭代
    for i in range(iternumber):
        h=1/(1+np.exp(-x_mat*w))
        dw=x_mat.T*(h-y_mat)
        w -= alpha*dw
    return w

x_mat,y_mat=getdata("数据集1.txt")
print("x_mat:",x_mat,x_mat.shape)
print("y_mat:",y_mat,y_mat.shape)
w=w_calc(x_mat,y_mat,0.001,10001)

print("w:",w)

#测试集和决策分界可视化
w0=w[0,0]
w1=w[1,0]
w2=w[2,0]
plotx1=np.arange(1,7,0.01)
plotx2=-w0/w2-w1/w2*plotx1
plt.plot(plotx1,plotx2,color="r",label="decision doundary")
print(x_mat,y_mat)
plt.scatter(x_mat[:,1][y_mat==0].A,x_mat[:,2][y_mat==0].A,marker="^",s=150,label="label=0")
plt.scatter(x_mat[:,1][y_mat==1].A,x_mat[:,2][y_mat==1].A,s=150,label="label=1")
plt.grid()
plt.legend()
plt.show()

#对输入数据进行分类
x1=float(input("输入x1:"))
x2=float(input("输入x2:"))
x_test=np.mat([[1,x1,x2]])
h_test=1/(1+np.exp(-x_test*w))
if h_test>0.5:
    print("y=1")
else:
    print("y=0")

决策树

（这里只讨论离散属性的决策树分析）

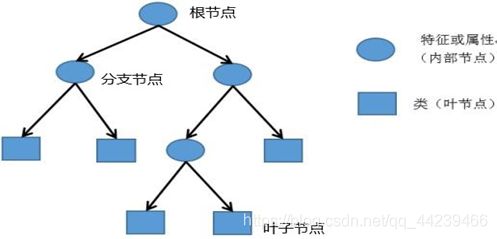
      决策树是机器学习的入门算法之一，也是目前在各种分类算法中最经常使用的算法。它的思想贯穿于我们生活的很多方面，哪怕一些不懂得机器学习，没做过相关学习的人也会使用它来完成一些任务的分类。说了这么多那么到底什么是决策树？，正如它的名字一样，决策树就是一颗树，和数据结构里的树一样，有根节点，分支节点，叶子节点。而在划分这些节点的时候我们加入了一些算法进行决策，最后划分成的树就叫做决策树。

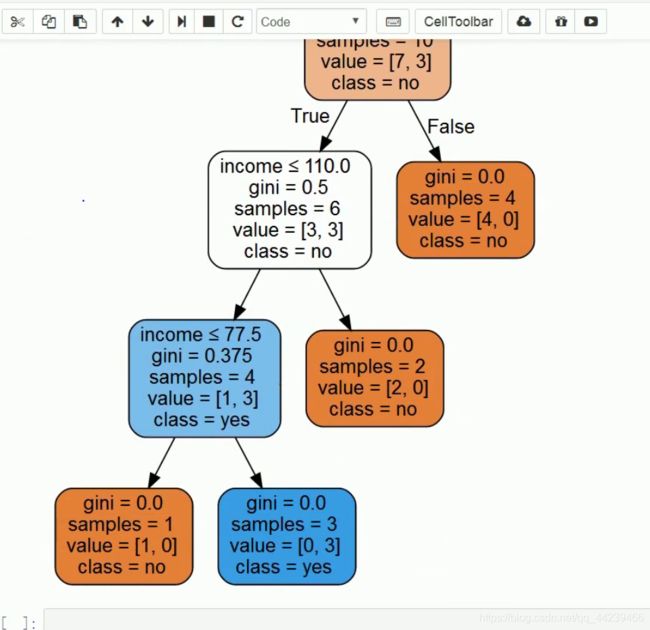
如图就是一颗决策树：

像一颗倒立的树。其中最上方的根节点就是数据集，而下面的分支节点就是对数据集的划分得到的子数据集，而下方子节点就是通过划分后确定为一类的数据，也就是每一个叶子节点都是一个类，叶子节点里的数据都是属于这一个类的。决策树的目的就是将总体数据划分到不同的类中，从而实现分类。

      那么如何对数据进行分类呢？这里有一个划分的标准：熵。熵是用来形容一个数据集不确定度的一个值，就是数据集中的类别越多熵就越大。决策树就是通过一层层划分将每一层的熵降低，逐渐提高数据纯度。

      熵的表达式为：

 

其中pi是概率，假设一个数据D,包含有{x1,x2,x3}三种数据类别，{p1,p2,p3}是其分别在D中占的比例，则对于D来说D的熵为：H=-p1logp1-p2logp2-p3logp3.

知道了熵之后那么我们要思考如何才能让熵通过一层层划分最快的降低呢。这里我们引入一个值：条件熵H(D|y)

设D有一个特征y，H(D|y)就是在知道y后根据y划分后的数据的熵。其表达式为:

      有了条件熵后我们就可以很容易的找到对数据进行划分的方法了，我们将D的每一个特征的条件熵都求出，哪一个相对于H(D)最小，哪一个在划分后熵的减少最大，我们便将它作为下一层的划分依据。

这可以用公式Gain(D,y) = H(D) – H(D|y)来计算它，并称之为信息增益。在划分时我们通过相减后取Gain最大的特征进行划分，并在划分出的分支中再找Gain最大的进行划分，如此类推，知道树划分到要求深度时停止，从而实现分类。

      以上过程就是决策树算法的创始人昆兰研究出的第一代算法，也被称为ID3算法，但是    ID3算法有一些地方存在缺陷，其中两个最重要的点就是

1. 无法对连续特征进行划分
2. 在求最大信息增益时如果某一特征x划分出的类别比另一个特征y划分出的类别多，那么x的信息增益就会比y的大

为了改善这些缺陷，昆兰又推出了改进的算法ID4.5。ID4.5不仅解决了处理连续特征值的问题，同时也通过改变选取特征值的标准消除了第二点缺点。在ID4.5中，选取信息增益比来作为选取标准。

信息增益比的公式：

通过除以A的特征熵来校正信息增益容易偏向于取值较多的特征的问题。而建立决策树的过程和ID3是相同的。

但是ID4.5仍有一些缺陷，例如：1.在构建决策树时使用的是多叉树而在计算机中二叉树的运算速度往往要比多叉树快很多，2.ID4.5对于熵的计算有大量的对数运算较为复杂，运算强度较大。而对于ID4.5的这些问题，我们思考怎么样才能简化模型，减少运算强度呢，我们注意到之前我们一直都在使用熵的运算来作为选择标准，现在产生了这样的问题，那我们能不能找到另外一个和熵的作用类似同时又使运算减少的模型呢？

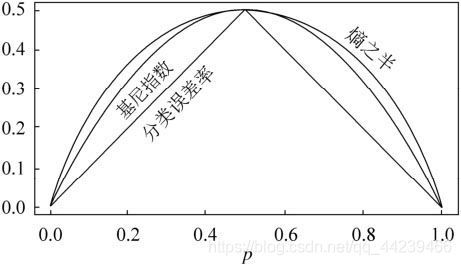
基于这个问题一个新决策树算法出现了：CART算法。CART算法使用基尼系数来代替信息增益比（基尼系数代表了模型的不纯度，基尼系数越小，则不纯度越低，特征越好。这和信息增益(比)是相反的）

如图我们可以看到基尼系数于熵之半的曲线非常接近，所以可以用基尼系数近似代替熵的模型。

这里我们假设D数据集里有k个类别，数据点属于第k个类别的有C个，则对于D来说基尼系数为：

CART算法就是根据每一个特征值，分别将数据分为两类，然后求相应的基尼系数进行比较。假设D根据A分成了两部分D1,D2。那么在根据A进行分类的基尼系数为：

 

如此对D的别的特征求基尼系数，哪一个的基尼系数小说明哪一个特征划分后数据的纯度高，便选取这个特征作为下一次的划分特征。

如此对划分出的分支继续这样划分，构建决策树。

但是还有一个问题是，怎么保证每一个特征都只能将数据分成两类？如果分成了四类五类呢？当数据被分成超过两类时，需要分别以将数据划分为几个类的划分点为数据集的二分点 ，将数据分成两类分别求划分为两类后子集的纯度Gini(D,Ai)，(其中Ai 表示特征A的可能取值)，然后从所有的可能的划分的Gini(D,Ai)中找出基尼系数最小的划分，这个划分的划分点，便是使用特征A对样本集合D进行划分的最佳划分点，按照这个划分点将数据分成两类。

这样的根据CART算法我们便构造出了一个二叉树式的决策树

随机森林。

另外，对于CART算法包括之前的ID4.5算法都有一个问题就是过拟合问题，具体就是把数据集中的噪声数据也分成了单独的类，这会使得决策树模型的泛化能力下降，分类的准确度下降，因此我们可以采取剪枝来增加泛化能力，可用预剪枝或者后剪枝，对于CART算法我们往往选择后剪枝先生成决策树，再生成经过剪枝后的决策树，再进行检验选择，具体可从文献三了解。

下面我们借助python实现CART算法的建立决策树对数据分类：

1. 仍然是用程序生成数据集这里我们以csv文件的形式储存。

 

#调用numpy库,机器学习库sklearn和生成决策树图形的graphviz库
from sklearn import tree
import numpy as np
import graphviz

#导入数据
data=np.genfromtxt("数据集2.csv",delimiter=",")
x_data=data[1:,1:-1]
y_data=data[1:,-1]

#创建决策树模型
model=tree.DecisionTreeClassifier()
model.fit(x_data,y_data)

#导出决策树
dot_data=tree.export_graphviz(model,out_file=None,feature_names=["house_yes","house_no","single","married","divorced","income"],
                              class_names=["no","yes"],filled=True,rounded=True,special_characters=True)

graph=graphviz.Source(dot_data)
graph.render("cart")

 

1. 导入数据并使用sklearn库的tree函数生成决策树

参考文献

文献一：https://blog.csdn.net/qq_19645269/article/details/79551576

文献二：http://blog.sciencenet.cn/blog-477629-822983.html

文献三：https://www.cnblogs.com/luban/p/9412339.html

逻辑回归参考文献：

https://blog.csdn.net/Artprog/article/details/51241581

https://www.jianshu.com/p/f89a19df2995

决策树参考文献：（算法公式配图主要来自第二个与第三个文档链接

 

https://www.cnblogs.com/sxron/p/5471078.html

https://shuwoom.com/?p=1452