CCF CSP刷题记录36——202006-4 1246（java）

 

【题目描述】 1,2,4,6 这四个数字有一个神奇的性质：如果将其分别取以 2 为底的幂，得到的分别是 2,4,16,64，仍是由这四个数字组成的。我们从数字串1 开始，每秒钟它的每一位都会独立地变成 2 的幂。

例如，在前几秒钟，数字串会依次变成：

1. 2
2. 4
3. 16
4. 264
5. 46416
6. 166416264
7. 264641626446416
8. 46416641626446416166416264
9. 166416264641626446416166416264264641626446416

显然，这些数字串都仅包含 1,2,4,6 这四个数字。输入整数 n 和数字串 S，请你求出 S 在第 n 秒钟的数字串共出现了几次？由于答案可能很大，只需要你输出它对 998244353 取模的结果。

【输入格式】 从标准输入读入数据。包含两行，第一行为一个数 n，第二行为一个串 S。
【输出格式】 输出到标准输出。仅有一行，含有一个整数，表示所求的答案。

【样例 1 输入】

9
26

【样例 1 输出】

5

【样例 1 解释】
第 9 秒的数字串为166416264641626446416166416264264641626446416，其中出现了5 次26。

【样例 2 输入】

2020
16

【样例 2 输出】

292008622

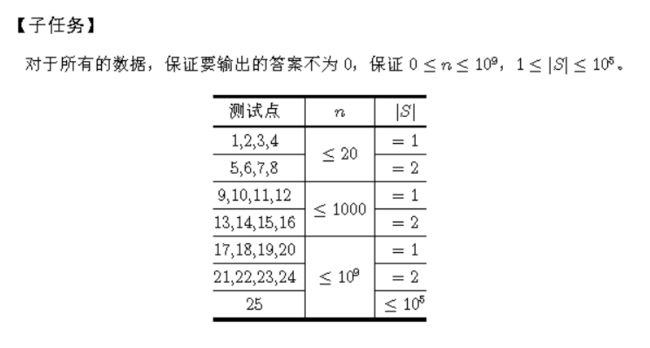
【数据范围】

这是我在网上看到的大佬的满分解法，我自己的代码就不贴了，暴力法就28分，太菜了( ´▽｀)

大佬的分析如下：

1. 按数位变化，我们可以基于数位思考；N = 10^9，时间复杂度要就是log(n)；
2. 基本上1个数位大概率会变2个。如果模拟法，没迭代一秒，字符串长度是指数增加的。可以过前8组测试。（可以写一下，快速拿分，并且在之后，用作新算法的基准测试用例对拍）
3. 所有数位都跳不出（1,2,4,6）这个集合。如果不考虑位置信息，其实就是一个线性递推问题。

 

dp[i][1] -> dp[i+1][2]
dp[i][2] -> dp[i+1][4]
dp[i][4] -> dp[i+1][1], dp[i+1][6]
dp[i][6] -> dp[i+1][6], dp[i+1][4]

把4个数字做一个离散化，变成(0,1,2,3)之后，很容易可以构建变换矩阵

0 1 0 0 
0 0 1 0
1 0 0 1
0 0 1 1

然后就是一个矩阵快速幂的模板
随后我们可以过掉所有|S| = 1的测试数据了。

1. 如果|S| > 1，我第一感觉是通过观察样例里的26，和前几组数字；发现26的个数等价于2秒前4的个数，所以所有长度大于2的数都先回退到长度为1的基本情况然后去带上减去的秒数，去算。
   比如26,9；等价于求4,7

 

多观察这个图很关键

这个做法在处理位数是2的CASE时候，发生了死循环；比如46-》66-》46成环了。
同时64-》42-》61-》44-》62-》41-》64 也是一个环

所以这个想法不WORK。在这里卡挺久的。
其实后来观察到单独针对2的CASE解出来，基本就拿到96分了。所以我的想法是对2位的数也建一个状态机。
比如

16-> 26,64
64-> 64,41,16
42-> 16,64

这样建变换矩阵的问题是会重复计算。
比如输入是264；会变成41 1次，64 2次 ， 61 1次， 16 1次
但是正确答案是41 1次，64 1次 ， 61 1次， 16 1次
原因是6单个数字就可以扩展成2位。所以在2位数的前一位是6和后一位是6生成的数字中会被重复计算。同时4也有这个问题。

然后想用容斥原理去解决掉重复计算的问题，比如4和6再最高位或最低位，直接不考虑。但是首字母和尾字母都可能会有4和6的情况。这样会漏掉解。当然如果是不用快速幂，而是线性迭代的话，这个问题是可以在递推过程中修正掉的。但是10^9这里要求我们的递推公式是不能有IF 的，必须是一个直接转移。

最后通过把1位和2位的状态结合在一起考虑列变换方程。发现可以不重不漏

1. 最后4分，写完前面的，很快就可以发现3位的输入，回溯到2位是没有环的。大喜。然后提交跑了个TLE，因为第一版回溯写法是暴力回溯，递归每一层只处理1个字母的回溯，枚举每一个可能性随后剪枝。
   通过进一步观察，我发现了一个性质，这个回溯的过程，其实只有在首字母是可能出现分叉。
   比如4，是可以由上一位的2过来，也可以是上一位6得来。这个确定了之后，余下的都是唯一解。如果走不通必然就无解。
   所以就优化了写法，最后AC了。

2. 变换矩阵如果很大，可以用代码生成，核心就是维护好A状态可以变换到哪些B状态。然后矩阵行代表FROM，矩阵列代表可以变换过去的TO，随后 mat[from][to]++
   小伙伴可以拉上去看看S=1时的矩阵就理解了。

大佬的满分代码如下：

import java.util.*;
public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        Main m = new Main();
        System.out.println(m.solve(sc.nextInt(), sc.next()));
    }
    int M = 998244353;
    int[] val2id = new int[67];
    int[] baseEle =   { 1,  2,     4,      6,     16,  26,  41,  42,  44,  46,  61,  62,  64,  66};
    int[][] convert = {
    {2},{4},{1,6,16},{6,4,64},{26},{46},{62},{64},{61},{66},{42},{44},{41},{46}};
    {
        Arrays.fill(val2id, -1);
        for (int i = 0; i < baseEle.length; i++) val2id[baseEle[i]] = i;
    }
    private int solve(int n, String s) {
        if (s.length() <= 2) return solveBase(val2id[Integer.parseInt(s)], n); // 96分
        else { // 4分
            int res = 0;
            for (int[] i : shorten(s, 0)) res = (res + solveBase(i[0], n - i[1])) % M;
            return res;
        }
    }
    
    private int solveBase(int id, int n) { // 矩阵快速幂
        int[][] init = new int[1][14]; init[0][0] = 1;
        int[][] mat = new int[14][14];
        for (int from  = 0; from < 14; from++) for (int to : convert[from]) mat[from][val2id[to]]++;
        while (n > 0) {
            if ((n & 1) == 1) init = mul(init, mat);
            mat = mul(mat, mat);
            n >>= 1;
        }
        return init[0][id];
    }

    private int[][] mul(int[][] a, int[][] b) { // 矩阵乘法
        int n = a.length, m = a[0].length, k = b[0].length;
        int[][] res = new int[n][k];
        for (int i = 0; i < n; i++)
            for (int j = 0; j < k; j++)
                for (int q = 0; q < m; q++)
                    res[i][j] = (int) ((res[i][j] + (long) a[i][q] * b[q][j] % M) % M);
        return res;
    }

    int[] ones = {'4', 6, '6', 4}; // 2种忽略掉16的1，和64的6的特殊情况
    private List shorten(String s, int dep) { // 回溯到上层；处理首字母，因为首字母可能有>1种情况
        if (s.length() <= 2) {
            int id = val2id[Integer.parseInt(s)];
            return id == -1 ? Collections.EMPTY_LIST : Arrays.asList(new int[]{id, dep});
        }
        List res = new ArrayList<>();
        for (int i = 0; i < ones.length; i += 2)
            if (ones[i] == s.charAt(0)) res.addAll(shorten(ones[i+1] + postShorten(s, 1), dep + 1));
        res.addAll(shorten(postShorten(s, 0), dep + 1));
        return res;
    }
    String[] pos = {"2", "4", "/", "16", "/", "64"};
    private String postShorten(String s, int idx) { // 唯一可能性的回溯，找不到就返回一个非法字符代表无解
        StringBuilder sb = new StringBuilder();
        while (idx < s.length()) {
            int i = 0;
            for (; i < pos.length; i++) {
                if (s.startsWith(pos[i], idx) || (idx == s.length() - 1 && pos[i].charAt(0) == s.charAt(idx))) {
                    idx += pos[i].length();
                    sb.append(i + 1);
                    break;
                }
            }
            if (i == pos.length) return "0"; // invalid number
        }
        return sb.toString();
    }
}

作者：西部小笼包
链接：https://www.jianshu.com/p/efc9e984eff0
来源：简书
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。