评价与量化CNN的各个卷积窗对于分类结果的贡献(论文解读)
引用:Xu, H., Chen, Y., Lin, R., & Kuo, C. (2018). Understanding convolutional neural networks via discriminant feature analysis. APSIPA Transactions on Signal and Information Processing, 7, E20. doi:10.1017/ATSIP.2018.24
本文引入了一些量化方式来分析CNN中的各层卷积窗对于最终分类结果的辨识能力,用作分析的网络为Fast-RCNN-CaffeNet。即Fast-RCNN的图像分类部分,卷积部分结构与CaffeNet类似。
摘要
概括:这篇文章采用两种方法来分析CNN不同层提取出的特征。首先,从数学角度上显示高斯混淆度量(Gaissian confusion measure, GCM)可以量化单一特征的分辨能力(discriminative ability)。然后,将这个概念推广,引入簇纯度度量(cluster purity measure,CPM)来量化多个特征的联合分辨能力。最后,比较不同CNN结构下训练的特征,以解释更深层网络的优越性。
正文
为了训练一个能够用作物体识别的CNN,显然我们需要将带有目标物体的图片作为训练数据进行训练。在第一层中,卷积层提取的是低阶的特征。随着不断进行池化,层数越深,卷积层能够提取的信息就越具有辨识性。
根据CaffeNet的结构,其第五层的卷积窗个数为256个。给定一个ROI区域,在五层卷积输出后,我们可以取得一个256*13*13的特征。对于每一个卷积窗,将其13*13的输出响应求取最大值,就可以将256*13*13的特征图化为一个256维的向量。向量的每一个值即为对应滤波器的响应值。
(1)高斯混淆度量
该度量可以量化单一卷积窗的分辨能力。
假定某一给定类别 c c c,拥有N个测试数据, 其中包括正例数据(属于类别 c c c)以及反例数据(不属于类别 c c c)。
对于一个给定测试样本 ( x i → , y i ) (\overrightarrow{x_i},y_i) (xi,yi),其中 x i → \overrightarrow{x_i} xi为ROI, y i y_i yi为标签。那么对于第 i i i个样本,在第 k k k个卷积层的第 j j j个卷积窗的响应值可以表示为 F i ( f k j ) F_i(f_{kj}) Fi(fkj)。
为了得出高斯混淆度量的值,我们需要得出在 c c c类下,正样本与负样本响应值的均值与标准差。给定一个卷积窗 f k j f_{kj} fkj,其正样本的均值与标准差为:
m 0 ( f k j , c ) = 1 N 0 ∑ ∀ i , s . t . y i = c F i ( f k j ) , σ 0 ( f k j , c ) = 1 N 0 ∑ ∀ i , s . t . y i = c [ F i ( f k j ) − m 0 ( f k j , c ) ] 2 m_0(f_{kj},c)=\frac{1}{N_0}\sum_{\forall i,s.t.y_i=c}F_i(f_{kj}),\\ \sigma_0(f_{kj},c)=\sqrt{\frac{1}{N_0}\sum_{\forall i,s.t.y_i=c}[F_i(f_{kj})-m_0(f_{kj},c)]^2} m0(fkj,c)=N01∀i,s.t.yi=c∑Fi(fkj),σ0(fkj,c)=N01∀i,s.t.yi=c∑[Fi(fkj)−m0(fkj,c)]2
对于负样本,公式与上类似。其中 N 0 N_0 N0表示正样本的个数。
然后,给定阈值 t t t,在 c c c类下,卷积窗 f k j f_{kj} fkj的错误率为:
Q k j ( t , c ) = ∫ − ∞ t N ( m 0 ( f k j , c ) , σ 0 ( f k j , c ) ) + ∫ t ∞ N ( m 1 ( f k j , c ) , σ 1 ( f k j , c ) ) Q_{kj}(t,c)=\int_{-\infin}^{t}N(m_0(f_{kj},c),\sigma_0(f_{kj},c))\\ + \int_{t}^{\infin}N(m_1(f_{kj},c),\sigma_1(f_{kj},c)) Qkj(t,c)=∫−∞tN(m0(fkj,c),σ0(fkj,c))+∫t∞N(m1(fkj,c),σ1(fkj,c))
建议 t t t为 m 0 , m 1 m_0,m_1 m0,m1的均值。然后,在多类别情况下,寻找类别 c g m c c_{gmc} cgmc使错误率为最小。
最后,高斯混淆度量可以表示为:
G C M ( f k j ) = Q k j ( t , c g m c ) E j [ Q k j ( t , c g m c ) ] / m 0 ( f k j , c g m c ) E j [ m 0 ( f k j , c g m c ) ] GCM(f_{kj})=\frac{Q_{kj}(t,c_{gmc})}{E_j[Q_{kj}(t,c_{gmc})]}/\frac{m_0(f_{kj},c_{gmc})}{E_j[m_0(f_{kj},c_{gmc})]} GCM(fkj)=Ej[Qkj(t,cgmc)]Qkj(t,cgmc)/Ej[m0(fkj,cgmc)]m0(fkj,cgmc)
该系数越大,表示该卷积窗的辨识度越差。
2)簇纯度度量
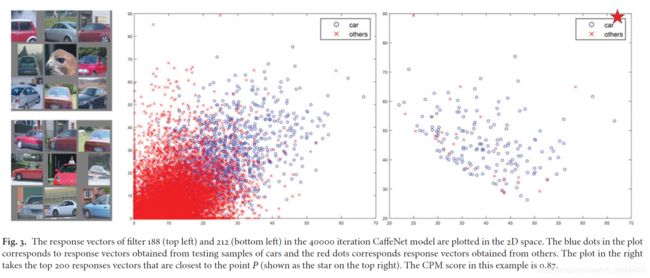
簇纯度度量解决了高斯混淆度量只能应用于单一卷积窗的劣势。给定第k层的一组卷积窗 f k j → , j → ∈ J f_{k\overrightarrow j,\overrightarrow j \in J} fkj,j∈J ,以及一个类别 c c c,假定这组卷积窗的数量是2,那么所有图像的响应值能够投在二维平面上。下图为示意图。
簇纯度度量的定义很简单:寻找各维度的最大值点(红色五角星),然后寻找离该点最近的K个点(此处K=200),其中正样本的比例就是所求的簇纯度度量。
文章下载链接:https://www.cambridge.org/core/journals/apsipa-transactions-on-signal-and-information-processing/article/understanding-convolutional-neural-networks-via-discriminant-feature-analysis/724A0FF83ED539AA7FA41D77F77479A8